Planification d'itinéraire

JaVelo – étape 6

1. Introduction

Le but principal de cette étape est d'écrire ce qui constitue la partie centrale du projet, à savoir le code permettant de planifier un itinéraire idéal pour se déplacer à vélo d'un point de départ à un point d'arrivée. Son but secondaire est d'écrire la classe représentant un itinéraire multiple, composé d'une séquence de sous-itinéraires.

Notez que cette étape devra être rendue deux fois :

pour le rendu testé habituel (délai : 1/4 17h00),
pour le rendu intermédiaire (délai : 8/4 17h00).

Le deuxième de ces rendus sera corrigé par lecture du code de vos étapes 1 à 6, et il vous faudra donc soigner sa qualité et sa documentation. Il est fortement conseillé de lire notre guide à ce sujet.

2. Concepts

2.1. Planification d'itinéraire

Le but de la planification d'itinéraire est de déterminer un itinéraire « idéal » allant d'un point de départ à un point d'arrivée. Dans un premier temps, on peut considérer que l'itinéraire idéal est simplement celui qui est le plus court.

La technique habituellement utilisée pour planifier un itinéraire consiste à rechercher le plus court chemin reliant un nœud de départ à un nœud d'arrivée dans le graphe représentant le réseau routier. Les nœuds de ce graphe correspondent aux intersections entre les routes, et les arêtes représentent les routes les reliant. Les arêtes sont annotées avec la longueur de la route qu'elles représentent.

Dans un tel graphe, un chemin entre un nœud de départ et un nœud d'arrivée est simplement une succession d'arêtes permettant d'aller du nœud de départ à celui d'arrivée. La longueur d'un chemin est la somme de la longueur des arêtes qui le composent, et le plus court chemin reliant deux nœuds est celui dont la longueur est la plus petite parmi tous les chemins existants. Il est bien entendu possible que le plus court chemin ne soit pas unique.

Il faut noter que le graphe JaVelo ne correspond pas exactement à la description ci-dessus, dans la mesure où ses nœuds ne représentent pas tous des intersections entre des routes. En fait, la plupart des nœuds du graphe JaVelo se trouvent entre deux intersections.

La présence de ces nœuds intermédiaire rend le graphe plus gros, et ralentit donc la recherche du plus court chemin. Ils permettent toutefois de simplifier le dessin de l'itinéraire, puisqu'ils décrivent la forme exacte des routes. De plus, la grande densité de nœuds intermédiaires permet d'en trouver plus facilement qui soient proches des points de départ et d'arrivée choisis par l'utilisateur.

2.2. Algorithme de Dijkstra

Un des algorithmes les plus connus pour déterminer le plus court chemin dans un graphe est l'algorithme de Dijkstra — du nom de son inventeur, l'informaticien néerlandais Edsger Dijkstra.

2.2.1. Compréhension intuitive

Pour comprendre intuitivement le fonctionnement de l'algorithme de Dijkstra, on peut utiliser l'analogie suivante. Imaginons que l'on désire trouver le plus court chemin entre le Château d'Ouchy et la tour d'observation de Sauvabelin. Pour ce faire, on pourrait dans un premier temps réunir un très grand nombre de personnes au point de départ — le Château d'Ouchy, visible sur la carte ci-dessous.

Une fois ce groupe de personnes réuni, on pourrait le diviser en autant de sous-groupes qu'il existe de routes partant du Château d'Ouchy. Admettons qu'il n'y en ait que trois : l'Avenue de Rhodanie qui part vers l'ouest, l'Avenue d'Ouchy qui part vers le nord, et le Quai de Belgique qui part vers l'est. Le groupe peut donc se séparer en trois parties égales, le premier sous-groupe suivant l'Avenue de Rhodanie, le second l'Avenue d'Ouchy et le dernier le Quai de Belgique. Chacun de ces groupes avance exactement à la même vitesse et s'arrête à chaque nouvelle intersection rencontrée.

Ainsi, le second sous-groupe, qui suit l'Avenue d'Ouchy vers le nord, va rencontrer une première intersection avec la Rue du Liseron (à l'ouest) et le Chemin de Beau-Rivage (à l'est) — ignorons, pour simplifier les choses, la Place du Port. A cet endroit, le sous-groupe peut à nouveau se séparer en trois : un sous-sous-groupe continue son chemin le long de la Rue du Liseron, un second le long de l'Avenue d'Ouchy, et un troisième le long du Chemin de Beau-Rivage.

Si tous les groupes avancent à la même vitesse et se séparent systématiquement à chaque intersection, alors il est certain que lorsqu'un groupe arrive en premier à une intersection, le chemin que ce groupe a suivi est le plus court chemin la reliant au point de départ. Dès lors, chaque fois qu'un groupe atteint une intersection, il peut y laisser une note indiquant quel chemin il a suivi pour y arriver. Bien entendu, un groupe ne doit faire cela que dans le cas où aucun autre groupe n'est parvenu à cette intersection précédemment, c.-à-d. si personne n'y a encore laissé de note. Si un groupe arrive à une intersection où une note se trouve déjà, alors il sait que le chemin qu'il a suivi jusque-là n'est pas le plus court, et ses membres peuvent rentrer à la maison.

En procédant de cette manière, il est garanti qu'à un moment donné, un groupe atteindra le point d'arrivée — la tour de Sauvabelin. Lorsque cela se produit, ce groupe a suivi le plus court chemin entre le point de départ et celui d'arrivée, qui est maintenant connu. Le groupe peut donc annoncer aux autres qu'il est arrivé à destination, et tout le monde peut rentrer à la maison.

2.2.2. Algorithme

L'algorithme de Dijkstra utilise fondamentalement la même idée que celle présentée ci-dessus, la différence étant que plutôt que de parcourir des routes, il parcourt un graphe dont les nœuds correspondent aux intersections, et les arêtes correspondent aux routes les reliant.

Cet algorithme est donné en pseudo-code ci-dessous. Ses paramètres sont le nœud de départ, Nd, et le nœud d'arrivée, Na. Comme dans JaVelo, ces nœuds sont des entiers positifs contigus.

Le tableau distance mémorise, pour chaque nœud, la distance du plus court chemin actuellement connu jusqu'à lui. Initialement, seule la distance du plus court chemin menant au nœud de départ est connue — et vaut bien entendu 0 —, les autres distances étant inconnues, donc infinies.

L'ensemble en_exploration contient les nœuds en cours d'exploration. Dans l'analogie de la section précédente, on peut voir cet ensemble comme étant celui des nœuds auxquels un groupe de personne se trouve actuellement, ou qu'un groupe va atteindre prochainement.

 1: pour chaque nœud N du graphe:
 2:   distance[N] = ∞
 3: 
 4: distance[Nd] = 0
 5: en_exploration = {Nd}
 6: tant que en_exploration n'est pas vide:
 7:   N = nœud de en_exploration tel que distance[N] minimale
 8:       (N est retiré de en_exploration)
 9:   si N = Na:
10:     terminer, car le plus court chemin a été trouvé
11:   pour chaque arête A sortant de N:
12:     N′ = nœud d'arrivée de A
13:     d = distance[N] + longueur de A
14:     si d < distance[N′]:
15:       distance[N′] = d
16:       ajouter N′ à en_exploration
17: 
18: terminer, car aucun chemin n'a été trouvé

Pour être sûr de bien comprendre le fonctionnement de cet algorithme, appliquez-le manuellement au graphe de la figure 1 ci-dessous pour trouver le plus court chemin entre le nœud de départ A et le nœud d'arrivée F. Dans cette figure, la distance actuelle à chaque nœud a été indiquée en rouge à côté de son nom, les valeurs indiquées étant celles juste avant le début de la boucle, à la ligne 5.

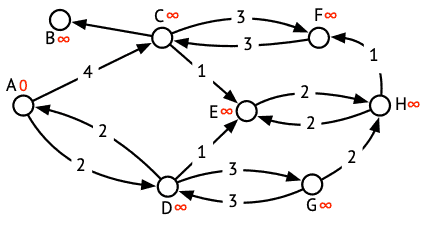
dijkstra-example;16.png — Figure 1 : Exemple de graphe

En plus des distances actuelles inscrites à côté de chaque nœud, gardez aussi trace du contenu de l'ensemble en_exploration, et indiquez clairement lequel des nœuds qu'il contient est sélectionné à chaque itération. Le tableau ci-dessous montre la valeur de cet ensemble durant les trois premières itérations, le nœud souligné étant sélectionné.

	`en_exploration`
1	{ A }
2	{ C, D }
3	{ C, E, G }
…	…

2.2.3. Reconstruction du chemin

L'algorithme donné plus haut détermine la plus courte distance entre le nœud de départ et celui d'arrivée mais ne calcule pas le chemin permettant d'aller de l'un à l'autre. Pour calculer ce chemin, il faut de plus mémoriser, pour chaque nœud, son prédécesseur dans le plus court chemin menant jusqu'à lui.

Cela implique deux ajouts à l'algorithme. Premièrement, lors de l'initialisation, le prédécesseur de chaque nœud est initialisé avec une valeur quelconque, par exemple 0. Les lignes 1 à 2 sont donc augmentées ainsi :

pour chaque nœud N du graphe:
  distance[N] = ∞
  prédécesseur[N] = 0

Deuxièmement, lorsque la distance du plus court chemin menant à un nœud est mise à jour, le prédécesseur de ce nœud doit également l'être. Les lignes 14 à 16 sont donc augmentées ainsi :

si d < distance[N′]:
  distance[N′] = d
  prédécesseur[N′] = N
  ajouter N′ à en_exploration

Grâce à l'information stockée dans prédécesseur, il est facile de reconstruire le plus court chemin lorsqu'on atteint le nœud d'arrivée. Il suffit en effet de partir de ce nœud d'arrivée et de remonter la chaîne des prédécesseurs jusqu'à arriver au nœud de départ.

2.2.4. Fonction de coût

Jusqu'à présent, nous avons admis que le chemin que nous désirions calculer était le chemin le plus court. Or en pratique, les planificateurs d'itinéraires utilisent plusieurs autres critères que la distance pour déterminer l'itinéraire idéal.

Par exemple, JaVelo ayant pour but d'être utilisé pour se déplacer à vélo, il semble logique qu'il préfère un itinéraire empruntant une route peu fréquentée à un itinéraire empruntant une route très fréquentée, même si ce dernier est plus court.

Une manière simple d'obtenir ce résultat consiste simplement à allonger artificiellement les arêtes correspondant à des routes peu désirables. Par exemple, on pourrait décider de multiplier par 1.5 la longueur de toutes les arêtes situées sur des routes nationales, peu agréables à parcourir à vélo.

On utilise pour cela une fonction de coût (cost function), qu'on applique à une arête et qui retourne un facteur supérieur ou égal à 1, par lequel la véritable longueur d'une arête est multipliée pour obtenir sa longueur « artificielle », utilisée lors du calcul du plus court chemin. Cette fonction de coût peut utiliser tous les attributs d'une arête pour déterminer le facteur correspondant : son dénivelé positif, les attributs OSM qui lui sont attachés, etc.

2.3. Algorithme A*

Note : cette section décrit un algorithme plus efficace que celui de Dijkstra, mais un peu plus difficile à programmer. Dans un premier temps, nous vous recommandons de l'ignorer, et de mettre en œuvre l'étape au moyen de l'algorithme de Dijkstra. Une fois que vous aurez terminé, testé et rendu votre étape, lisez cette section pour voir comment améliorer votre recherche d'itinéraire.

Lorsqu'on l'utilise pour rechercher le plus court chemin dans un graphe représentant un réseau routier, l'algorithme de Dijkstra a une limitation qui le rend sous-optimal : il ne tient pas compte de la position des nœuds dans l'espace pour orienter la recherche.

Dans l'analogie de la §2.2.1, cela se traduit par le fait qu'une partie des participants à la recherche du chemin le plus court entre le Château d'Ouchy et la tour de Sauvabelin suit la route du bord du lac en direction de Vevey. Or il est évident qu'en faisant cela, ils s'éloignent de plus en plus du point d'arrivée, et plus ils s'en éloignent, plus la probabilité qu'ils soient en train de suivre le plus court chemin diminue.

Pour tenir compte de cet aspect, on peut imaginer choisir le prochain nœud à explorer non pas uniquement en fonction de la longueur du chemin qui le relie au nœud de départ, mais aussi en fonction de la distance à vol d'oiseau qui le sépare du nœud d'arrivée. Cette distance à vol d'oiseau représente la distance minimale qu'il faut encore parcourir pour atteindre le nœud d'arrivée, car il est évident qu'aucune route ne peut être plus directe que la ligne droite.

Cette idée est celle de l'algorithme A* — prononcé « A étoile » en français, « A star » en anglais. Pour la mettre en œuvre, il suffit d'ajuster l'algorithme de la §2.2.2 afin qu'il choisisse comme prochain nœud à explorer celui minimisant la somme de la distance du plus court chemin jusqu'à lui et de la distance à vol d'oiseau jusqu'au nœud d'arrivée.

3. Mise en œuvre Java

3.1. Classe `MultiRoute`

La classe MultiRoute du sous-paquetage routing, publique et immuable, représente un itinéraire multiple, c.-à-d. composé d'une séquence d'itinéraires contigus nommés segments. Elle implémente l'interface Route et possède un unique constructeur public :

MultiRoute(List<Route> segments), qui construit un itinéraire multiple composé des segments donnés, ou lève IllegalArgumentException si la liste des segments est vide.

En dehors de ce constructeur, la classe MultiRoute ne possède que les définitions concrètes des méthodes abstraites de l'interface Route, à savoir :

int indexOfSegmentAt(double position), qui retourne l'index du segment de l'itinéraire contenant la position donnée ;
double length(), qui retourne la longueur de l'itinéraire, en mètres,
List<Edge> edges(), qui retourne la totalité des arêtes de l'itinéraire,
List<PointCh> points(), qui retourne la totalité des points situés aux extrémités des arêtes de l'itinéraire, sans doublons,
PointCh pointAt(double position), qui retourne le point se trouvant à la position donnée le long de l'itinéraire,
double elevationAt(double position), qui retourne l'altitude à la position donnée le long de l'itinéraire, qui peut valoir NaN si l'arête contenant cette position n'a pas de profil,
int nodeClosestTo(double position), qui retourne l'identité du nœud appartenant à l'itinéraire et se trouvant le plus proche de la position donnée,
RoutePoint pointClosestTo(PointCh point), qui retourne le point de l'itinéraire se trouvant le plus proche du point de référence donné.

Comme celles de SingleRoute, toutes les méthodes prenant des positions doivent en accepter une quelconque : une position négative est considérée comme équivalente à 0, tandis qu'une position supérieure à la longueur de l'itinéraire est considérée comme équivalente à cette longueur.

3.1.1. Conseils de programmation

La plupart des méthodes de MultiRoute s'expriment en terme des méthodes correspondantes des segments. Par exemple, la méthode length de MultiRoute appelle la méthode length des différents segments, et combine les résultats. Il en va de même des autres méthodes.

En particulier, notez que indexOfSegmentAt doit également faire appel à la méthode du même nom d'un des segments, qui pourrait lui aussi être un itinéraire multiple. Par exemple, on peut imaginer un itinéraire multiple composé de deux sous-itinéraires multiples, chacun composé de trois sous-sous-itinéraires simples de 1000 m. Dans une telle configuration, appeler indexOfSegmentAt sur l'itinéraire multiple avec une position de 5500 m doit retourner l'index 5.

Contrairement aux itinéraires simples, souvent composés de plusieurs centaines, voire de milliers d'arêtes, les itinéraires multiples ne devraient pas être composés de nombreux segments lors d'une utilisation normale de JaVelo. Dès lors, les méthodes de MultiRoute peuvent se permettre de recalculer leur résultat à chaque appel, et n'ont pas besoin d'utiliser de techniques de mise en œuvre sophistiquées comme celles décrites à la §3.2.1 de l'étape 5.

3.2. Interface `CostFunction`

L'interface CostFunction du sous-paquetage routing, publique, représente une fonction de coût. Elle n'est dotée que d'une méthode abstraite :

double costFactor(int nodeId, int edgeId), qui retourne le facteur par lequel la longueur de l'arête d'identité edgeId, partant du nœud d'identité nodeId, doit être multipliée ; ce facteur doit impérativement être supérieur ou égal à 1.

Notez que le facteur de coût peut être infini (Double.POSITIVE_INFINITY), ce qui exprime le fait que l'arête ne peut absolument pas être empruntée. Cela équivaut à considérer que l'arête n'existe pas.

Attention : l'argument edgeId passé à costFactor est l'identité de l'arête, et pas son index dans la liste des arêtes sortant du nœud d'identité nodeId. En d'autres termes, il s'agit d'un entier compris entre 0 et le nombre d'arêtes dans le graphe. Bien évidemment, l'arête portant cette identité doit être l'une des arêtes sortant du nœud d'identité nodeId.

3.3. Classe `CityBikeCF` (fournie)

La classe CityBikeCF, du sous-paquetage routing, public, représente la fonction de coût adaptée à la pratique du vélo. Elle implémente bien entendu l'interface CostFunction.

Cette fonction de coût vous est fournie dans une archive Zip à importer dans votre projet. Elle est très fortement inspirée de celle utilisée par défaut dans BRouter, un planificateur d'itinéraire cyclable.

3.4. Classe `RouteComputer`

La classe RouteComputer du sous-paquetage routing, publique et immuable, représente un planificateur d'itinéraire. Elle possède un unique constructeur public :

RouteComputer(Graph graph, CostFunction costFunction), qui construit un planificateur d'itinéraire pour le graphe et la fonction de coût donnés.

En plus de ce constructeur, RouteComputer offre une unique méthode publique :

Route bestRouteBetween(int startNodeId, int endNodeId), qui retourne l'itinéraire de coût total minimal allant du nœud d'identité startNodeId au nœud d'identité endNodeId dans le graphe passé au constructeur, ou null si aucun itinéraire n'existe. Si le nœud de départ et d'arrivée sont identiques, lève IllegalArgumentException.

Si plusieurs itinéraires de coût total minimal existent, bestRouteBetween retourne n'importe lequel d'entre eux.

3.4.1. Conseils de programmation

La méthode bestRouteBetween n'étant pas très simple à programmer, nous vous conseillons fortement de procéder ainsi :

écrire une première version utilisant l'algorithme de Dijkstra, plus simple,
vérifier qu'elle fonctionne correctement, en utilisant les indications de la §3.5.1,
rendre votre projet — pour passer les tests, l'algorithme utilisé importe peu,
incorporer les optimisations décrites ci-dessous, et utiliser l'algorithme A*.

Ces optimisations, y compris l'utilisation de l'algorithme A*, seront prises en compte lors du rendu intermédiaire. Seuls les groupes les ayant toutes mises en œuvre pourront espérer recevoir la totalité des points attribués à cette étape. Elles n'ont toutefois aucune importance pour les tests unitaires.

File de priorité
Tel que présenté à la §2.2, l'algorithme de Dijkstra stocke les nœuds en cours d'exploration dans un ensemble nommé en_exploration. À chaque itération, le prochain nœud à explorer doit en être retiré, ce qui implique un parcours de tous les éléments de l'ensemble.

Il est possible de faire mieux en utilisant une file de priorité (priority queue) pour stocker les nœuds en cours d'exploration plutôt qu'un ensemble. Une file de priorité est une file dont les éléments sont ordonnés, et dont le plus petit élément peut être retiré de manière efficace. En Java, la classe PriorityQueue représente une telle file, et l'extrait de test JUnit ci-dessous illustre son utilisation :
```
PriorityQueue<Integer> p = new PriorityQueue<>();
p.addAll(List.of(5, 2, 17, 29, 33, 1, 8));
assertEquals(1, p.remove());
assertEquals(2, p.remove());
assertEquals(5, p.remove());
```
Comme on le voit, les éléments sont insérés dans la file dans un ordre quelconque, mais chaque appel à remove retourne — et supprime de la file — le plus petit d'entre eux.

Pour utiliser une telle file dans l'algorithme de Dijkstra, il faut pouvoir y stocker les nœuds en cours d'exploration, triés par distance. Cela implique de définir un enregistrement, nommé p. ex. WeightedNode, contenant à la fois l'identité d'un nœud et sa distance. Dans la file, ces enregistrements doivent être triés par distance. Pour garantir cela, il faut utiliser des concepts qui n'ont pas encore été vus au cours, et nous vous donnons donc ici la définition de l'enregistrement :
```
record WeightedNode(int nodeId, float distance)
    implements Comparable<WeightedNode> {
  @Override
  public int compareTo(WeightedNode that) {
    return Float.compare(this.distance, that.distance);
  }
}
```
Notez que, aussi bizarre que cela puisse paraître, cet enregistrement peut très bien être déclaré directement à l'intérieur de la méthode bestRouteBetween ! En effet, Java tolère les déclarations d'enregistrements à l'intérieur de méthodes :
```
public Route bestRouteBetween(…) {
  record WeightedNode(…)
      implements Comparable<WeightedNode> { … }
}
```
Nœuds visités

Une propriété de l'algorithme de Dijkstra (et de A*) est que lorsqu'un nœud a été exploré, c.-à-d. qu'il a été extrait de l'ensemble en_exploration et que ses arêtes sortantes ont été parcourues, le plus court chemin jusqu'à lui est connu et il ne sera donc plus jamais nécessaire de l'explorer à nouveau.

L'algorithme présenté à la §2.2 n'explore naturellement plus ces nœuds, puisque la condition de la ligne 14 n'est plus jamais vraie pour eux. Toutefois, il est plus efficace de marquer ces nœuds d'une manière ou d'une autre, et de les ignorer dès l'instant où on les extrait de en_exploration.

Cela peut se faire de manière assez efficace en stockant une valeur spéciale pour ces nœuds dans le tableau distance, p. ex. Float.NEGATIVE_INFINITY. Lorsqu'un nœud est extrait de en_exploration et que sa distance est égale à cette valeur spéciale, alors il est simplement ignoré. Cela évite d'évaluer inutilement sa fonction de coût.

3.5. Tests

Comme d'habitude, nous ne vous fournissons pas de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.

3.5.1. Planification d'itinéraire

Pour tester votre planificateur, nous vous conseillons de visualiser sur une carte les itinéraires qu'il produit. Une manière simple de faire cela consiste à générer un fichier au format KML — un type de fichier textuel permettant de décrire des données géographiques — puis de visualiser ce fichier KML sur une carte.

La classe KmlPrinter ci-dessous offre une méthode write prenant un nom de fichier et un itinéraire, et écrivant la description de l'itinéraire au format KML dans le fichier. Un exemple de son utilisation est donné plus bas.

public final class KmlPrinter {
  private static final String KML_HEADER =
    "<?xml version=\"1.0\" encoding=\"UTF-8\"?>\n" +
    "<kml xmlns=\"http://www.opengis.net/kml/2.2\"\n" +
    "     xmlns:gx=\"http://www.google.com/kml/ext/2.2\">\n" +
    "  <Document>\n" +
    "    <name>JaVelo</name>\n" +
    "    <Style id=\"byBikeStyle\">\n" +
    "      <LineStyle>\n" +
    "        <color>a00000ff</color>\n" +
    "        <width>4</width>\n" +
    "      </LineStyle>\n" +
    "    </Style>\n" +
    "    <Placemark>\n" +
    "      <name>Path</name>\n" +
    "      <styleUrl>#byBikeStyle</styleUrl>\n" +
    "      <MultiGeometry>\n" +
    "        <LineString>\n" +
    "          <tessellate>1</tessellate>\n" +
    "          <coordinates>";

  private static final String KML_FOOTER =
    "          </coordinates>\n" +
    "        </LineString>\n" +
    "      </MultiGeometry>\n" +
    "    </Placemark>\n" +
    "  </Document>\n" +
    "</kml>";

  public static void write(String fileName, Route route)
      throws IOException {
    try (PrintWriter w = new PrintWriter(fileName)) {
      w.println(KML_HEADER);
      for (PointCh p : route.points())
	w.printf(Locale.ROOT,
		 "            %.5f,%.5f\n",
		 Math.toDegrees(p.lon()),
		 Math.toDegrees(p.lat()));
      w.println(KML_FOOTER);
    }
  }
}

Les fichiers KML obtenus peuvent être visualisés sur le site map.geo.admin.ch. Il suffit pour cela d'ouvrir ce site dans un navigateur puis de glisser le fichier KML dessus.

Le programme ci-dessous illustre l'utilisation des classes développées jusqu'à présent pour déterminer le meilleur itinéraire entre l'EPFL et Sauvabelin, plus précisément entre :

le nœud JaVelo 159049 (correspondant au nœud OSM 335535677) et
le nœud JaVelo 117669 (correspondant au nœud OSM 8787891978).

La description de cet itinéraire ensuite écrite dans le fichier KML nommé javelo.kml.

public final class Stage6Test {
  public static void main(String[] args) throws IOException {
    Graph g = Graph.loadFrom(Path.of("lausanne"));
    CostFunction cf = new CityBikeCF(g);
    RouteComputer rc = new RouteComputer(g, cf);
    Route r = rc.bestRouteBetween(159049, 117669);
    KmlPrinter.write("javelo.kml", r);
  }
}

En affichant le fichier KML obtenu sur une carte, vous devriez voir ceci :

Notez que le fond de carte gris a été utilisé ci-dessus, pour faciliter la visualisation de l'itinéraire.

3.5.2. Performances

Afin de tester les performances de votre recherche d'itinéraire, nous mettons à votre disposition les données couvrant environ le tiers ouest de la Suisse. Ces données sont fournies sous la forme d'une archive Zip qui a la même structure que celle de l'étape 4, si ce n'est que le répertoire contenant les fichiers se nomme ch_west. La zone couverte par ces données est visible sur cette carte.

Attention : comme la zone est différente, les nœuds JaVelo n'ont pas les mêmes identités que dans les données lausannoise !

Une fois ces données importées dans votre projet, vous pouvez modifier le programme de test plus haut pour lui faire rechercher un itinéraire entre :

le nœud JaVelo 2046055 (OSM 3524096459), à la gare de Lausanne,
le nœud JaVelo 2694240 (OSM 420347107), à la gare de Boncourt.

Cette recherche devrait prendre environ une seconde sur un ordinateur récent lorsque toutes les optimisations mentionnées plus haut ont été mises en œuvre. Pour mesurer le temps de calcul assez précisément, vous pouvez utiliser la méthode nanoTime de System, ainsi :

RouteComputer rc = …;
long t0 = System.nanoTime();
Route r = rc.bestRouteBetween(2046055, 2694240);
System.out.printf("Itinéraire calculé en %d ms\n",
		  (System.nanoTime() - t0) / 1_000_000);

L'animation ci-dessous illustre la recherche de cet itinéraire par les algorithme A* (en rouge) et Dijkstra (en gris), les points colorés correspondant aux nœuds visités.

4. Résumé

Pour cette étape, vous devez :

écrire les classes MultiRoute et RouteComputer ainsi que l'interface CostFunction selon les indications données ci-dessus,
tester votre code,
documenter la totalité des entités publiques que vous avez définies,
rendre votre code au plus tard le 1 avril 2022 à 17h00, via le système de rendu.

Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.

N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !