Itinéraires simples et calcul de profil

JaVelo – étape 5

1. Introduction

Le but de cette étape est d'écrire la classe représentant un itinéraire simple, ainsi que celle permettant de calculer le profil d'un itinéraire quelconque à partir des profils de ses arêtes.

2. Concepts

Nous avons vu à l'étape précédente que, dans le graphe JaVelo, un itinéraire n'est rien d'autre qu'une séquence d'arêtes permettant de relier les points de passage entre eux. Les sections suivantes expliquent comment effectuer deux opérations importantes sur un tel itinéraire :

déterminer son profil en long à partir des profils de ses arêtes, et
déterminer le point de l'itinéraire se trouvant le plus près d'un autre point dans son voisinage.

2.1. Calcul d'un profil en long d'un itinéraire

À première vue, calculer le profil en long d'un itinéraire semble trivial : il suffit de mettre bout à bout les profils de ses arêtes, et le tour est joué. Malheureusement, deux problèmes rendent cette opération plus complexe qu'il n'y paraît :

les arêtes représentant des tunnels ou des ponts n'ont pas de profil,
la distance séparant les échantillons des profils des arêtes varie d'une arête à l'autre.

La figure 1 plus bas illustre ces problèmes avec un itinéraire très simple composé de quatre arêtes, représentées par les flèches noires au sommet.

Le profil de chaque arête est dessiné en rouge au-dessous d'elle. Dans tous les cas il s'agit d'une fonction échantillonnée donnant l'altitude (a) en fonction de la distance (d), sauf pour la troisième arête, qui n'a pas de profil.

Finalement, en bas de la figure est dessiné en bleu le profil de l'itinéraire complet. Il s'agit d'une unique fonction échantillonnée obtenue à partir des profils individuels.

Figure 1 : Profil en long d'un itinéraire

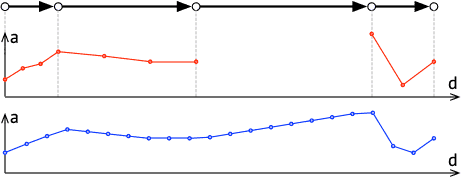
Notez bien que les échantillons du profil de l'itinéraire sont espacés régulièrement, comme d'habitude. En conséquence, ils ne correspondent généralement pas à des échantillons des profils des arêtes, mais ont été obtenus de deux manières : ceux situés sur une arête dotée d'un profil l'ont été par interpolation des échantillons du profil de l'arête, tandis que ceux situés sur une arête sans profil l'ont été par interpolation entre les échantillons extrêmes des arêtes voisines.

2.2. Calcul du point le plus proche d'une référence

Lorsqu'on utilise JaVelo et qu'on place le pointeur de la souris dans le voisinage d'un itinéraire, le point de l'itinéraire qui en est le plus proche est mis en évidence. On le voit dans la copie d'écran ci-dessous, où le point de l'itinéraire rouge le plus proche du pointeur est représenté par un disque blanc à bord rouge.

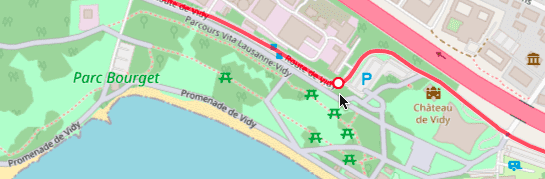
route-point-highlight;64.png — Figure 2 : Mise en évidence du point le plus proche du curseur

Pour mettre ce comportement en œuvre, il faut pouvoir déterminer le point d'un itinéraire le plus proche d'une référence donnée — p. ex. le pointeur de la souris.

Pour comprendre comment faire cela, on peut commencer par constater que si l'itinéraire était une droite, alors déterminer le point sur cette droite le plus proche d'une référence donnée serait trivial : il suffirait de projeter perpendiculairement la référence sur la droite. Cette idée est illustrée dans la figure ci-dessous, qui montre une droite, trois points de référence P₁ à P₃ et, en rouge, les points de la droite les plus proches de chacun d'eux.

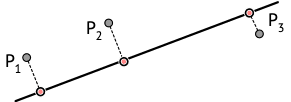
line-closest-point;32.png — Figure 3 : Points les plus proches sur une droite

Sachant qu'une arête est un segment de droite, on peut adapter cette idée pour déterminer le point d'une arête le plus proche d'un point de référence. En effet, si la projection de ce point de référence sur la droite qui prolonge l'arête se trouve sur l'arête elle-même, alors cette projection est le point de l'arête le plus proche de la référence. Sinon, le point de l'arête le plus proche de la référence est l'une des extrémités de l'arête.

Cette idée est illustrée dans la figure ci-dessous qui montre une arête, la droite qui la prolonge, et les trois mêmes points de référence que ci-dessus. Le point de l'arête le plus proche de P₁ est son point de départ, celui le plus proche de P₃ est son point d'arrivée, et celui le plus proche de P₂ est le même que dans la figure précédente.

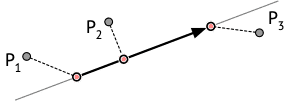
edge-closest-point;32.png — Figure 4 : Points les plus proches sur une arête

Comme un itinéraire est constitué d'une séquence d'arêtes, déterminer le point de l'itinéraire le plus proche d'un point de référence peut donc se faire facilement. Il suffit de parcourir les arêtes, déterminer pour chacune d'elles son point le plus proche de la référence, et garder parmi tous ces points celui dont la distance à la référence est la plus petite.

3. Mise en œuvre Java

Étant donné que toutes les entités — classes, interfaces, etc. — du projet appartiennent au paquetage ch.epfl.javelo ou à l'un de ses sous-paquetages, nous omettrons désormais la partie ch.epfl.javelo des noms de paquetages. Ainsi, lorsqu'on parle ci-dessous du sous-paquetage routing, on entend ch.epfl.javelo.routing.

3.1. Classe `ElevationProfileComputer`

La classe ElevationProfileComputer du sous-paquetage routing, publique, finale et non instanciable, représente un calculateur de profil en long. C'est-à-dire qu'elle contient le code permettant de calculer le profil en long d'un itinéraire donné.

Ce calcul est fait par la méthode publique (et statique) suivante :

ElevationProfile elevationProfile(Route route, double maxStepLength), qui retourne le profil en long de l'itinéraire route, en garantissant que l'espacement entre les échantillons du profil est d'au maximum maxStepLength mètres ; lève IllegalArgumentException si cet espacement n'est pas strictement positif.

Le nombre d'échantillons se calcule en arrondissant par excès (vers le haut) le résultat de la division de la longueur de l'itinéraire par l'espacement maximum entre les échantillons, puis en ajoutant 1 au résultat. Ce calcul garantit que l'espacement entre échantillons est aussi grand que possible, mais néanmoins inférieur ou égal à la limite demandée.

3.1.1. Conseils de programmation

La principale difficulté rencontrée lors de l'écriture de la méthode elevationProfile est celle de la gestion des valeurs manquantes, dues aux arêtes dénuées de profil.

Il faut noter que les arêtes dénuées de profil possèdent néanmoins une méthode elevationAt, mais elle retourne systématiquement la valeur NaN (not a number). Il est toutefois possible de les traiter de la même manière que les autres arêtes dans un premier temps, puis de traiter les valeurs NaN dans un deuxième temps. C'est ce que nous vous conseillons fortement de faire, en décomposant donc le calcul du profil en deux étapes consistant à :

créer et remplir le tableau des échantillons du profil de l'itinéraire en appelant simplement la méthode elevationAt de l'itinéraire,
remplir les « trous » dans ce tableau des échantillons, en remplaçant les valeurs NaN qu'il contient par des valeurs interpolées.

La création et le remplissage initial du tableau d'échantillons ne pose aucun problème étant donné l'existence de la méthode elevationAt de Route.

Le remplissage des « trous », qui consiste à remplacer les éventuelles valeurs NaN du tableau par des altitudes, se fait quant à lui par interpolation. La seule exception à cette règle est le cas dégénéré où le tableau initial ne contient que des trous, auquel cas on admet que le profil est à l'altitude constante de 0 mètres.

Pour remplir les trous, nous vous conseillons de procéder en trois phases successives :

Rechercher le premier échantillon valide du tableau — c.-à-d. la première valeur différente de NaN — et l'utiliser pour « boucher » tous les trous en tête du tableau, grâce à la méthode fill de Arrays. Si ce premier échantillon valide n'existe pas car le tableau ne contient que des trous, les remplir tous avec l'altitude 0.
Procéder de manière similaire pour boucher les trous en queue du tableau des échantillons avec le dernier échantillon valide — qui existe forcément.
Parcourir le tableau par ordre croissant d'index afin de trouver les trous intermédiaires et les remplir par interpolation linéaire à partir des valeurs valides situées des deux côtés du trou — qui existent forcément.

Pour déterminer si un élément du tableau est une valeur NaN, vous devez utiliser la méthode isNaN de Float. Notez en particulier que l'égalité ne fonctionne pas dans ce cas, car NaN == NaN retourne faux !

3.2. Classe `SingleRoute`

La classe SingleRoute du sous-paquetage routing, publique et immuable (donc finale), représente un itinéraire simple, c.-à-d. reliant un point de départ à un point d'arrivée, sans point de passage intermédiaire. Elle implémente l'interface Route.

SingleRoute offre un unique constructeur public :

SingleRoute(List<Edge> edges), qui retourne l'itinéraire simple composé des arêtes données, ou lève IllegalArgumentException si la liste d'arêtes est vide.

En plus de ce constructeur, SingleRoute ne fournit que les versions concrètes des méthodes abstraites de l'interface Route, à savoir :

int indexOfSegmentAt(double position), qui retourne l'index du segment de l'itinéraire contenant la position donnée, qui vaut toujours 0 dans le cas d'un itinéraire simple,
double length(), qui retourne la longueur de l'itinéraire, en mètres,
List<Edge> edges(), qui retourne la totalité des arêtes de l'itinéraire,
List<PointCh> points(), qui retourne la totalité des points situés aux extrémités des arêtes de l'itinéraire,
PointCh pointAt(double position), qui retourne le point se trouvant à la position donnée le long de l'itinéraire,
double elevationAt(double position), qui retourne l'altitude à la position donnée le long de l'itinéraire, qui peut valoir NaN si l'arête contenant cette position n'a pas de profil,
int nodeClosestTo(double position), qui retourne l'identité du nœud appartenant à l'itinéraire et se trouvant le plus proche de la position donnée,
RoutePoint pointClosestTo(PointCh point), qui retourne le point de l'itinéraire se trouvant le plus proche du point de référence donné.

Toutes les méthodes prenant des positions — pointAt, elevationAt et nodeClosestTo — doivent accepter une position quelconque : une position négative est considérée comme équivalente à 0, tandis qu'une position supérieure à la longueur de l'itinéraire est considérée comme équivalente à cette longueur.

3.2.1. Conseils de programmation

La méthode pointAt doit être efficace, car elle est destinée à être appelée à chaque mouvement de la souris dans la version finale du programme. Pour cette raison, elle ne peut pas se contenter de parcourir la liste des arêtes pour déterminer sur laquelle d'entre elles se trouve le point demandé. Au lieu de cela, elle doit déterminer l'index de cette arête par recherche dichotomique dans un tableau contenant la position de chacun des nœuds le long de l'itinéraire.

Pour illustrer cette idée, nous utiliserons l'itinéraire représenté dans la figure 5 ci-dessous, doté de six nœuds — numérotés en rouge de 0 à 5 — et donc de cinq arêtes — numérotées en bleu de 0 à 4.

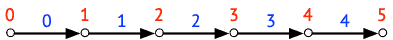
route-binary-search;16.png — Figure 5 : Itinéraire de six nœuds / cinq arêtes

Les arêtes font respectivement 5800, 2300, 1100, 2200 et 1700 mètres de long. Dans un souci de simplicité, la figure ci-dessus ne les représente pas à l'échelle.

La position le long de l'itinéraire du nœud 0 est de 0 m. Celle du nœud 1 est de 5800 m. Celle du nœud 2 est de 8100 m (5800 + 2300). Et ainsi de suite. Ces positions peuvent être placées dans un tableau dont l'index est celui d'un nœud de l'itinéraire, et la valeur est la position de ce nœud le long de l'itinéraire, en mètres. Pour l'exemple ci-dessus, ce tableau est :

Index	0	1	2	3	4	5
Position	0	5800	8100	9200	11400	13100

Par construction, un tel tableau est toujours trié par ordre croissant, son premier élément vaut toujours 0, et son dernier élément est toujours égal à la longueur totale de l'itinéraire, ici 13.1 km.

Le fait que le tableau soit trié par ordre croissant implique qu'il est possible d'y faire une recherche dichotomique pour trouver efficacement — en \(O(\log n)\) — une valeur particulière. Une telle recherche permet également de déterminer où il faudrait insérer une valeur donnée qui n'existe pas dans le tableau, ce qui permet de savoir entre quelle paire de nœuds se trouve une position donnée.

La figure 6 ci-dessous illustre cela en donnant, en noir, les valeurs retournées par la méthode binarySearch de Arrays — qui fait une recherche dichotomique dans un tableau — lorsqu'on l'utilise pour rechercher une position donnée dans le tableau plus haut.

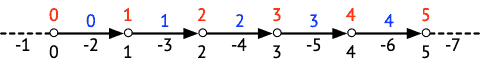
route-binary-search-annotated;16.png — Figure 6 : Recherche dichotomique le long d'un itinéraire

Comme on le voit, lorsque la position passée à binarySearch correspond exactement à celle d'un nœud, alors elle retourne une valeur positive ou nulle donnant l'index de ce nœud. Lorsque cette position se trouve entre deux nœuds, elle retourne une valeur négative à partir de laquelle il est simple d'obtenir l'index de l'arête sur laquelle se trouve la position.

Par exemple, en appelant binarySearch avec le tableau plus haut et la position 10000, on obtient -5. Le fait que cette valeur soit négative signifie que 10000 ne se trouve pas dans le tableau, mais que sa place y serait entre les index 3 et 4 — voir la documentation de binarySearch pour plus de détails. On en conclut que cette position se trouve sur l'arête 3, à la position 800 (10000-9200). En appelant la méthode pointAt de l'arête 3 de l'itinéraire avec 800 en argument, on obtient donc le point se trouvant à la position 10000 de l'itinéraire.

Les méthodes elevationAt et nodeClosestTo peuvent s'écrire de manière similaire à pointAt.

3.3. Tests

Comme pour l'étape précédente, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.

4. Résumé

Pour cette étape, vous devez :

écrire les classes ElevationProfileComputer et SingleRoute selon les indications données ci-dessus,
tester votre code,
documenter la totalité des entités publiques que vous avez définies,
rendre votre code au plus tard le 25 mars 2022 à 17h00, via le système de rendu.

Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.

N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !