Routes et chemins
tCHu – étape 2
1. Introduction
Le premier but de cette étape est de terminer l'écriture des classes représentant les principaux éléments du jeu, en écrivant celle représentant une route. Cette classe sera ensuite utilisée pour en écrire une seconde, représentant un chemin et capable entre autres de calculer le plus long chemin du réseau d'un joueur.
Avant de commencer à travailler à cette étape, lisez le guide Sauvegarder son travail. Il vous donnera des conseils importants concernant la sauvegarde de votre projet au cours du semestre.
2. Concepts
2.1. Routes
Les gares, décrites à l'étape précédente, sont reliées entre elles par ce que nous nommerons des routes (routes), qui constituent le réseau ferroviaire. Ces routes sont de différentes longueurs, simples ou doubles, colorées ou neutres, en surface ou en tunnel. Ces caractéristiques sont visibles sur l'extrait de réseau ci-dessous, et détaillées dans les sections qui suivent.
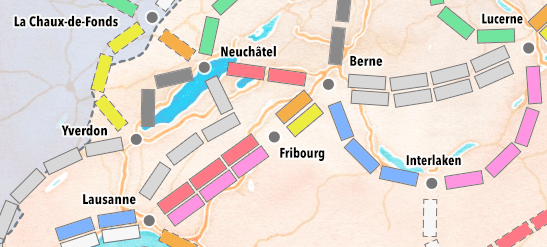
2.1.1. Longueur
La longueur d'une route est le nombre de cases qui la compose, qui est toujours compris entre 1 et 6 (inclus). Par exemple, la route reliant Neuchâtel à Yverdon est de longueur 2, tandis que celle reliant Neuchâtel à Lausanne est de longueur 4.
2.1.2. Multiplicité
Une route peut être simple ou double. Par exemple, la route reliant Neuchâtel à Berne est simple, tandis que celle reliant Fribourg à Berne est double.
2.1.3. Couleur
Certaines routes sont colorées, tandis que d'autres sont neutres. Les routes colorées le sont au moyen des mêmes huit couleurs que celles utilisées pour les cartes wagon, à savoir : noir, violet, bleu, vert, jaune, orange, rouge, et blanc.
Par exemple, la route reliant Neuchâtel à Yverdon est noire, tandis que celle reliant Neuchâtel à Lausanne est neutre, raison pour laquelle elle est dessinée en gris clair sur la carte.
Les routes doubles colorées le sont toujours au moyen de deux couleurs différentes, comme celle reliant Fribourg à Berne, constituée d'une route orange et d'une route jaune. Les routes doubles neutres sont toujours constituées de deux routes neutres, comme celle reliant Berne à Lucerne.
2.1.4. Niveau
Certaines routes sont en tunnel, tandis que d'autres sont en surface. Les routes en tunnel se reconnaissent à leur contour traitillé.
Par exemple, la route reliant Neuchâtel à Lausanne est en surface, tandis que celle reliant Neuchâtel à La Chaux-de-Fonds est en tunnel.
2.2. Prise de possession d'une route
Comme nous l'avons vu, un des principaux buts des joueurs de tCHu est de s'emparer de routes afin de relier des gares entre elles. Les règles concernant la prise de possession d'une route, décrites dans les sections suivantes, sont très simples pour les routes en surface, mais un peu plus complexes pour les routes en tunnel.
Lorsqu'un joueur s'empare d'une route, il obtient immédiatement des points dits « de construction » (claim points), qui dépendent de la longueur de la route, selon la table suivante :
| Longueur | Points |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 7 |
| 5 | 10 |
| 6 | 15 |
2.2.1. Route en surface
Pour pouvoir s'emparer d'une route en surface, un joueur doit posséder :
- un nombre de wagons au moins égal à la longueur de la route,
- un nombre de cartes wagon de même couleur que la route au moins égal à la longueur de la route.
Si la route est neutre, les cartes wagon utilisées pour s'en emparer peuvent être de couleur quelconque, mais unique.
Si un joueur désirant s'emparer d'une route en surface dispose des cartes et wagons nécessaire, il peut le faire en se défaussant des cartes puis en plaçant un de ses wagons sur chacune des cases constituant la route. Pour mémoire, les wagons sont symbolisés par des rectangles colorés — en bleu clair ( m ) pour le joueur 1 et en rose ( m ) pour le joueur 2 — ornés de deux disques blancs.
L'image ci-dessous illustre la prise de possession, par le joueur 2, de la moitié rouge de la route Lausanne - Fribourg, qui est en surface.
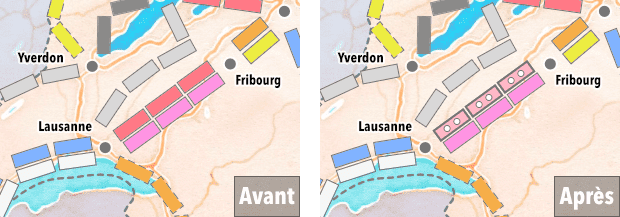
Dès qu'un joueur s'est emparé d'une route, son adversaire n'a bien entendu plus la possibilité de le faire. D'autre part, dès qu'un joueur s'est emparé d'une des deux moitiés d'une route double, l'autre est condamnée et personne ne peut s'en emparer.
2.2.2. Route en tunnel
Pour pouvoir s'emparer d'un tunnel, un joueur doit remplir les mêmes conditions que pour une route en surface. Dans le cas d'un tunnel, il peut toutefois aussi utiliser les cartes locomotive, qui sont en quelque sorte multicolores et peuvent donc jouer le rôle d'une carte wagon de couleur quelconque.
Si un joueur désirant s'emparer d'un tunnel dispose des cartes et wagons nécessaires, il doit tout d'abord placer devant lui les cartes qu'il désire utiliser, après quoi les trois cartes se trouvant au sommet de la pioche sont retournées. Ces trois cartes déterminent les éventuelles cartes additionnelles que le joueur doit jouer, en plus de celles qu'il a déjà posées, pour pouvoir s'emparer du tunnel.
Ainsi, chacune des trois cartes retournées qui est soit une carte wagon de même couleur qu'une carte posée initialement, soit une carte locomotive, implique l'utilisation d'une carte additionnelle. Ces cartes additionnelles peuvent être soit des cartes wagon de la même couleur que celles utilisées initialement, soit des cartes locomotive.
Si le joueur possède les cartes additionnelles nécessaires, et s'il accepte de les jouer, alors il peut s'emparer du tunnel. S'il ne possède pas les cartes, ou ne désire pas les jouer, il reprend toutes les cartes en main et termine son tour.
Notez qu'il est parfaitement possible de n'utiliser que des cartes locomotives pour tenter de s'emparer d'un tunnel. Dans ce cas, seules les éventuelles cartes locomotive figurant parmi les trois cartes retournées impliquent l'utilisation de cartes additionnelles, qui doivent alors obligatoirement être des locomotives.
2.2.3. Exemple de prise de possession d'un tunnel
Pour illustrer la prise de possession d'un tunnel, imaginons qu'un joueur désire s'emparer de celui reliant Neuchâtel à La Chaux-de-Fonds, orange et de longueur 1. Pour ce faire, admettons qu'il pose devant lui une carte orange qu'il a en main. Les trois cartes au sommet de la pioche sont alors retournées.
Supposons que ces trois cartes soient une orange, une verte et une locomotive. Elles impliquent que le joueur doit encore jouer deux cartes additionnelles s'il veut s'emparer du tunnel — une pour la carte orange, une pour la locomotive. Chacune de ces deux cartes peut être soit une carte orange, soit une locomotive.
Si le joueur avait décidé d'utiliser initialement une carte locomotive pour tenter de s'emparer du tunnel, alors les mêmes trois cartes retournées impliqueraient l'ajout d'une seule carte additionnelle — pour la locomotive —, mais celle-ci ne pourrait qu'être une locomotive.
2.3. Chemins
Un chemin (trail) dans le réseau d'un joueur donné est une séquence alternée de gares \(s_i\) et de routes \(r_i\) de la forme suivante :
\[ s_0\,r_1\,s_1\,r_2\,s_2\,\ldots\,r_n\,s_n \]
et telle que :
- toutes les routes appartiennent au joueur,
- la route \(r_i\) relie les gares \(s_{i-1}\) et \(s_i\),
- les routes sont distinctes deux à deux.
Notez bien que même si les routes d'un chemin doivent être distinctes, les gares ne doivent pas forcément l'être. Un chemin peut donc passer plusieurs fois par la même gare, mais il ne peut pas emprunter plusieurs fois la même route.
La longueur d'un chemin est la somme de la longueur des routes qui le compose.
L'image ci-dessous montre le réseau d'un joueur, en bleu, dans lequel les routes ont été nommées de A à F pour simplifier la discussion.
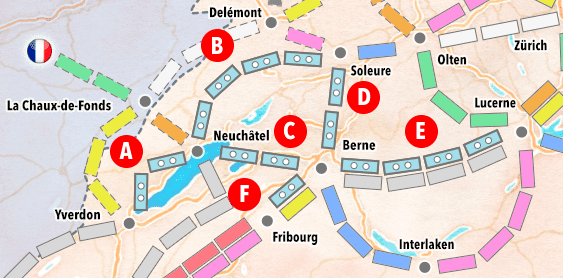
De très nombreux chemins existent dans ce réseau, parmi lesquels figurent les suivants (chaque chemin est suivi de sa longueur entre parenthèses) :
- Yverdon A Neuchâtel B Soleure D Berne E Lucerne (12),
- Neuchâtel C Berne D Soleure B Neuchâtel A Yverdon (10),
- Soleure D Berne (2),
- etc.
Par contre, les séquences suivantes ne sont pas des chemins :
- Neuchâtel C Berne D Soleure B Neuchâtel C Berne E Lucerne (invalide car la route C apparaît deux fois),
- Neuchâtel C Berne F Fribourg E Lucerne (invalide car E ne relie pas Fribourg à Lucerne)
- etc.
Pour alléger la notation, les gares intermédiaires d'un chemin peuvent être omises car il est possible de les déterminer sans ambiguïté. Par exemple, le premier chemin donné en exemple ci-dessus peut s'écrire simplement ainsi :
Yverdon ABDE Lucerne
En fait, dès qu'un chemin comporte au moins deux routes, les gares des extrémités peuvent également être déterminées sans ambiguïté. Dès lors, le chemin ci-dessus peut également s'écrire simplement ABDE, ce que nous ferons plus bas.
2.3.1. Plus long chemin
À la fin d'une partie de tCHu, le joueur dont le réseau comporte le plus long chemin remporte un bonus de 10 points. Si les plus longs chemins des deux joueurs sont de même longueur, le bonus leur est attribué à tous les deux.
Déterminer le plus long chemin du réseau d'un joueur est un problème plus difficile qu'il n'y paraît. À notre connaissance, il n'existe pas d'algorithme plus efficace qu'une recherche exhaustive. Cela dit, au vu de la petite taille et de la faible complexité des réseaux de tCHu, une telle recherche peut se faire assez rapidement.
Comme son nom l'indique, la recherche exhaustive consiste simplement à énumérer la totalité des chemins possibles dans un réseau, afin de déterminer lequel d'entre eux est le plus long.
L'énumération de tous les chemins possibles se fait en commençant avec les chemins les plus simples possibles — constitués d'une seule route — puis en essayant de les prolonger de toutes les manières possibles, en leur ajoutant des routes adjacentes, jusqu'à ce que cela ne soit plus possible. Sous forme de pseudo-code, cette énumération s'exprime ainsi :
cs = liste des chemins constitués d'une seule route
tant que cs n'est pas vide :
cs' = liste vide
pour tout chemin c de cs :
rs = (routes appartenant au joueur,
n'appartenant pas à c, et
pouvant prolonger c)
pour toute route r de rs :
ajouter c prolongé de r à cs'
cs = cs'
L'idée de cet algorithme est qu'au début de l'itération \(n\) de la boucle extérieure, l'ensemble cs contient tous les chemins possibles constitués de exactement \(n\) routes. L'union de tous ces ensembles cs constitue la totalité des chemins possibles du réseau.
Souvenez-vous que la longueur d'un chemin n'est pas égale au nombre de routes qui le composent, mais bien à la somme des longueurs de ces routes. Dès lors, et contrairement à ce qu'on pourrait initialement penser, le plus long chemin ne sera pas forcément produit lors de la dernière itération de la boucle extérieure.
L'algorithme ci-dessus ne fait rien d'autre qu'énumérer tous les chemins possibles, sans se souvenir du plus long. Il est toutefois facile de le modifier dans ce but, ce qui est laissé en exercice.
2.3.2. Exemple
Le fonctionnement de l'algorithme de recherche exhaustive peut être illustré au moyen du réseau de la figure 3. Pour faciliter la lecture, ce réseau est à nouveau présenté ci-dessous.

La liste cs est initialisée avec les chemins constitués d'une seule route. Comme il y a 6 routes dans le réseau, cs est initialisé avec 12 chemins, parmi lesquels on trouve :
- Neuchâtel A Yverdon
- Yverdon A Neuchâtel
- Neuchâtel B Soleure
- Soleure B Neuchâtel
- etc.
Lors de la première itération de la boucle extérieure, les 12 chemins contenus dans cs peuvent chacun être prolongés de différentes manières. Par exemple, le second chemin de la liste, Yverdon A Neuchâtel, peut être prolongé de deux manières différentes pour obtenir les chemins :
- Yverdon AB Soleure (noté simplement AB),
- Yverdon AC Berne (noté simplement AC).
Notez bien que la prolongation d'un chemin se fait toujours par ajout d'une route à la fin des routes existantes, pas au début.
Le tableau ci-dessous montre l'ensemble des chemins cs au début de chacune des 5 itérations de la boucle extérieure. La première ligne correspond à la valeur initiale de cet ensemble. Notez que les éléments de la liste cs ont été triés par ordre alphabétique pour faciliter la lecture, mais cet ordre ne joue aucun rôle et peut être quelconque.
| n | cs |
|---|---|
| 1 | A A B B C C D D E E F F |
| 2 | AB AC BA BC BD CA CB CD CE CF DB DC DE DF EC ED EF FC FD FE |
| 3 | ABD ACD ACE ACF BCD BCE BCF BDC BDE BDF CBD CDB DBA DBC DCA DCB ECA ECB EDB FCA FCB FDB |
| 4 | ABDC ABDE ABDF ACDB BDCA CBDE CBDF CDBA DBCE DBCF ECBD EDBA EDBC FCBD FDBA FDBC |
| 5 | ECBDF EDBCF FCBDE FDBCE |
En calculant la longueur de ces différents chemins, on constate que ceux constituant l'ensemble cs au début de la cinquième et dernière itération de l'algorithme ont tous une longueur de 13, supérieure à la longueur de tous les autres chemins. Il s'agit de :
- ECBDF (Lucerne - Berne - Neuchâtel - Soleure - Berne - Fribourg),
- EDBCF (Lucerne - Berne - Soleure - Neuchâtel - Berne - Fribourg),
- FCBDE (Fribourg - Berne - Neuchâtel - Soleure - Berne - Lucerne),
- FDBCE (Fribourg - Berne - Soleure - Neuchâtel - Berne - Lucerne).
Tous ces chemins méritent donc le titre de « chemin le plus long » du réseau, et n'importe lequel d'entre eux peut donc être produit en résultat.
3. Mise en œuvre Java
Avant de commencer à écrire le code de cette étape, il vous faut importer dans votre projet le contenu d'une archive Zip que nous vous fournissons et qui contient trois classes, Constants, ChMap et SortedBag. Ces classes sont rapidement décrites ci-dessous, avant celles que vous devez écrire vous-même.
Si l'importation de ces classes vous pose problème, reportez-vous à notre guide à ce sujet pour IntelliJ ou pour Eclipse.
3.1. Classe Constants (fournie)
La classe non instanciable Constants, du paquetage ch.epfl.tchu.game, contient la totalité des constantes liées aux règles du jeu. Par exemple, elle contient une constante entière nommée INITIAL_TICKETS_COUNT, qui représente le nombre de billets que chaque joueur reçoit en début de partie (5).
Ces constantes nommées doivent impérativement être utilisées à la place de leur valeur dans votre projet. Cela rend votre code à la fois plus lisible et plus facile à modifier.
Chacune des constantes de la classe Constants est accompagnée d'un commentaire Javadoc. Avant de continuer, lisez la totalité de ces commentaires afin de savoir quelles constantes sont à votre disposition.
3.2. Classe ChMap (fournie)
La classe non instanciable ChMap du paquetage ch.epfl.tchu.game décrit les gares, routes et billets de tCHu. Notez qu'elle utilise la classe Route que vous devez définir dans le cadre de cette étape, et Eclipse/IntelliJ vous signalera donc des erreurs tant et aussi longtemps que vous n'aurez pas au moins défini cette classe et son constructeur.
ChMap fournit les trois méthodes statiques suivantes :
List<Station> stations(), qui retourne la liste de toutes les gares de tCHu,List<Route> routes(), qui retourne la liste de toutes les routes de tCHu,List<Ticket> tickets(), qui retourne la liste de tous les billets de tCHu.
Cette classe vous est fournie car elle est fastidieuse et peu intéressante à écrire. Il faut toutefois noter que sa rédaction a été faite de manière méthodique, et que les noms et identités des éléments qu'elle contient ont été choisis de la manière suivante :
- les attributs (constants et privés) contenant les gares ont un nom composé de trois lettres majuscules, qui sont :
- pour les gares suisses, les trois premières lettres du nom de la ville (p.ex.
LAUpour Lausanne), sauf en cas de conflit, auquel cas les deux premières et la dernière lettre du nom sont utilisés (p.ex. entre Schaffhouse et Schwyz, pour lesquelles les nomsSCEetSCZont été utilisés), - pour les gares des pays voisins, le code à deux lettres du pays (selon la norme ISO 3166-1, soit
DEpour l'Allemagne,ATpour l'Autriche,ITpour l'Italie etFRpour la France) suivi d'un chiffre identifiant la gare ; les chiffres sont attribués en fonction de la position de la gare sur la carte, dans le sens horaire,
- pour les gares suisses, les trois premières lettres du nom de la ville (p.ex.
- une route est identifiée par l'abbréviation des deux gares qu'elle relie, suivi d'un chiffre qui vaut 1 pour la première composante de la route, et 2 pour la seconde, s'il s'agit d'une route double (p.ex.
LAU_NEU_1pour la première [et unique] route reliant Lausanne à Neuchâtel) ; notez que les deux gares reliées sont toujours données dans l'ordre alphabétique (p.ex.LAU_NEUet pasNEU_LAU).
Pour être sûr de bien comprendre cette classe, prenez un moment pour la lire et trouver où et comment sont définis les éléments suivant :
- la gare de Lausanne (quel est son numéro d'identification ?),
- la route reliant Fribourg à Berne (quelle est son identification textuelle ?),
- le billet Berne - pays voisins décrit à l'étape 1 (comment sont construits les 17 trajets qui le composent ?).
3.3. Classe SortedBag (fournie)
Attention : pour la suite de cette étape, vous devez savoir utiliser la généricité Java. Dès lors, si vous n'avez pas encore visionné ou lu le cours sur la généricité, faites-le avant de continuer.
La classe SortedBag, du paquetage ch.epfl.tchu, représente un multiensemble trié (sorted multiset ou sorted bag en anglais).
Un multiensemble trié sert de conteneur à un certain nombre d'objets d'un type donné, exactement comme ArrayList. Il s'agit donc de ce que l'on nomme habituellement une collection, concept qui sera examiné prochainement au cours.
Comparé à ArrayList, la classe SortedBag a toutefois deux différences importantes :
- elle trie automatiquement les éléments qu'elle contient — au même titre que la classe
TreeSetque vous avez utilisée à l'étape précédente, et qui représente elle un ensemble simple d'éléments (par opposition à un multiensemble), - elle est immuable, ce qui implique que ses méthodes ont un comportement et un type très différent des méthodes similaires de
ArrayList.
L'impact que ces deux caractéristiques ont sur la classe SortedBag est décrit ci-après.
3.3.1. Tri des éléments
Pour qu'une instance de SortedBag puisse trier les éléments qu'elle contient, ces éléments doivent être comparables deux à deux. Cela signifie qu'il doit être possible, étant donné deux éléments, de déterminer si le premier est plus petit que le second, si les deux sont égaux, ou si le premier est plus grand que le second. Notez que la méthode equals de Object ne suffit pas pour cela, car lorsque deux objets sont différents, elle ne permet pas de savoir lequel est le plus grand.
En Java, l'interface Comparable est destinée à être implémentée par les classes dont les éléments sont comparables. Pour une raison qui sera expliquée ultérieurement au cours, cette interface est générique, mais vous pouvez pour l'instant ignorer la signification de son paramètre de type. La seule méthode de Comparable est compareTo, qui compare le récepteur (this) à l'élément du même type passé en argument et indique s'ils sont égaux ou, sinon, lequel est le plus grand.
Afin de garantir que ses éléments sont comparables, et donc qu'ils implémentent l'interface Comparable, SortedBag place une borne supérieure sur son paramètre de type E. Sa déclaration ressemble donc à ceci :
class SortedBag<E extends Comparable<E>> { /* … */ }
Cette déclaration peut être comprise de la manière suivante : « SortedBag peut stocker des éléments d'un type quelconque, appelé E, à condition toutefois que ces éléments soient comparables entre eux au moyen de la méthode compareTo de Comparable. »
En plus de la classe elle-même, les différentes variantes de sa méthode de construction statique of, qui sont aussi génériques, placent la même borne sur leur paramètre de type à elles — que nous avons choisi de nommer également E, mais qui n'est pas pour autant le paramètre de type de la classe. Ainsi, la première variante de cette méthode est déclarée de la manière suivante :
static <E extends Comparable<E>> SortedBag<E> of() { /* … */ }
3.3.2. Immuabilité
Le fait que SortedBag soit immuable implique que les méthodes qui « modifient » le contenu du multiensemble ne le modifient bien entendu pas, mais retournent un nouveau multiensemble. Il est très important de garder cela en tête !
Par exemple, la méthode union permet de calculer l'union de deux multiensembles et est donc similaire à la méthode addAll de ArrayList, mais avec une différence de taille : alors que addAll modifie le récepteur (this) en lui ajoutant les éléments de l'argument, union ne modifie pas le récepteur mais retourne un nouveau multiensemble. Pour cette raison, addAll ne retourne rien — son type de retour est void — tandis que union retourne une valeur de type SortedBag.
Pour faciliter la construction progressive de multiensembles, SortedBag est accompagnée d'un bâtisseur nommé Builder, imbriqué dans SortedBag. L'exemple ci-dessous, similaire à celui donné à l'étape précédente pour illustrer l'utilisation de TreeSet, montre comment ce bâtisseur peut être utilisé pour construire le multiensemble des mots to be or not to be :
SortedBag.Builder<String> wordsB = new SortedBag.Builder<>();
for (String w: List.of("to","be","or","not","to","be"))
wordsB.add(w);
SortedBag<String> words = wordsB.build();
// s est égale à "{2×be, not, or, 2×to}"
String s = words.toString();
Cet exemple illustre le fait que les éléments d'un multiensemble trié sont toujours triés (ici dans l'ordre alphabétique), exactement comme avec un ensemble de type TreeSet. Par contre, il est possible qu'un même élément figure plusieurs fois dans un multiensemble, comme les mots be et to dans cet exemple, qui y apparaissent chacun 2 fois (d'où le préfixe 2× dans la représentation textuelle). Pour mémoire, un ensemble simple (p.ex. de type TreeSet) ne contient quant à lui jamais de doublons.
3.3.3. Méthodes à disposition
Afin d'avoir une idée des méthodes offertes par la classe SortedBag, lisez maintenant la totalité des commentaires Javadoc qui leur sont attachés. Bien entendu, vous avez également le droit de lire le code de ces méthodes, mais soyez conscients qu'elles utilisent de nombreux concepts qui n'ont pas encore été vus au cours, et il est donc probable que vous ne compreniez pas tout.
Dans cette étape et les suivantes, nous vous indiquerons les méthodes de SortedBag à utiliser dans les différents contextes, il n'est donc pas nécessaire d'essayer de les mémoriser.
3.4. Classe Route
La classe Route du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente une route reliant deux villes voisines.
Elle possède un type énuméré imbriqué public nommé Level, représentant les deux niveaux auquel une route peut se trouver. Ses valeurs sont, dans l'ordre :
OVERGROUND(route en surface),UNDERGROUND(route en tunnel).
En Java, un type énuméré imbriqué se définit de la même manière qu'une classe imbriquée statiquement. L'attribut static est toutefois optionnel dans ce cas, car les types énumérés sont forcément imbriqués statiquement. Le début de la définition de la classe Route ressemble donc à ceci :
public final class Route {
public enum Level { /* … valeurs du type énuméré */ }
// … reste de la classe Route
}
La classe Route offre un unique constructeur public :
Route(String id, Station station1, Station station2, int length, Level level, Color color), qui construit une route avec l'identité, les gares, la longueur, le niveau et la couleur donnés ; lèveIllegalArgumentExceptionsi les deux gares sont égales (au sens de la méthodeequals) ou si la longueur n'est pas comprise dans les limites acceptables (fournies par l'interfaceConstants), ouNullPointerExceptionsi l'identité, l'une des deux gares ou le niveau sont nuls. Notez bien que la couleur peut par contre être nulle, ce qui signifie que la route est de couleur neutre.
L'identité de la route passée au constructeur est une chaîne quelconque permettant d'identifier de manière unique la route. Il faudrait donc que chaque instance de Route créée ait une identité différente, mais cela n'est pas vérifié. L'utilité de l'identité des routes, comme celle de l'identité des gares, deviendra claire ultérieurement1.
En plus du constructeur, la classe Route offre les méthodes publiques suivantes :
String id(), qui retourne l'identité de la route,Station station1(), qui retourne la première gare de la route,Station station2(), qui retourne la seconde gare de la route,int length(), qui retourne la longueur de la route,Level level(), qui retourne le niveau auquel se trouve la route,Color color(), qui retourne la couleur de la route, ounulls'il s'agit d'une route de couleur neutre,List<Station> stations(), qui retourne la liste des deux gares de la route, dans l'ordre dans lequel elles ont été passées au constructeur,Station stationOpposite(Station station), qui retourne la gare de la route qui n'est pas celle donnée, ou lèveIllegalArgumentExceptionsi la gare donnée n'est ni la première ni la seconde gare de la route,List<SortedBag<Card>> possibleClaimCards(), qui retourne la liste de tous les ensembles de cartes qui pourraient être joués pour (tenter de) s'emparer de la route, trié par ordre croissant de nombre de cartes locomotive, puis par couleur,int additionalClaimCardsCount(SortedBag<Card> claimCards, SortedBag<Card> drawnCards), qui retourne le nombre de cartes additionnelles à jouer pour s'emparer de la route (en tunnel), sachant que le joueur a initialement posé les cartesclaimCardset que les trois cartes tirées du sommet de la pioche sontdrawnCards; lève l'exceptionIllegalArgumentExceptionsi la route à laquelle on l'applique n'est pas un tunnel, ou sidrawnCardsne contient pas exactement 3 cartes2,int claimPoints(), qui retourne le nombre de points de construction qu'un joueur obtient lorsqu'il s'empare de la route.
Faites bien attention au fait que l'ordre des éléments de la liste retournée par possibleClaimCards est spécifié et vous êtes donc tenus de le respecter. Par exemple, si on applique cette méthode à une route en tunnel de couleur neutre et de longueur 2, elle doit retourner une liste de 17 éléments qui sont, dans l'ordre :
| Index | Cartes |
|---|---|
| 0 | deux cartes wagon noires |
| 1 | deux cartes wagon violettes |
| … | … |
| 7 | deux cartes wagon blanches |
| 8 | une carte wagon noire, une carte locomotive |
| 9 | une carte wagon violette, une carte locomotive |
| … | … |
| 15 | une carte wagon blanche, une carte locomotive |
| 16 | deux cartes locomotive |
Les couleurs sont ordonnées selon l'ordre de définition du type énuméré Color.
3.4.1. Conseils de programmation
La méthode possibleClaimCards n'est pas très facile à écrire, donc réfléchissez bien à une solution avant de tenter de la programmer ! En particulier, notez qu'il est tout à fait possible de directement générer les ensembles de carte possibles dans l'ordre demandé, ce qui évite de devoir trier la liste avant de la retourner. Nous vous suggérons fortement de songer à une solution de ce type.
3.5. Classe Trail
La classe Trail du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente un chemin dans le réseau d'un joueur.
Elle ne possède aucun constructeur public, mais offre une méthode statique permettant d'obtenir le plus long chemin d'un réseau :
Trail longest(List<Route> routes), qui retourne le plus long chemin du réseau constitué des routes données ; s'il y a plusieurs chemins de longueur maximale, celui qui est retourné n'est pas spécifié ; si la liste des routes données est vide, retourne un chemin de longueur zéro, dont les gares sont toutes deux égales ànull.
En plus de cette méthode, la classe Trail offre les méthodes d'accès publiques suivantes :
int length(), qui retourne la longueur du chemin,Station station1(), qui retourne la première gare du chemin, ounullsi (et seulement si) le chemin est de longueur zéro,Station station2(), qui retourne la dernière gare du chemin, ounullsi (et seulement si) le chemin est de longueur zéro.
De plus, la classe Trail redéfinit la méthode toString afin qu'elle retourne une représentation textuelle du chemin, qui doit au moins contenir le nom de la première et de la dernière gare (dans cet ordre) ainsi que la longueur du chemin entre parenthèses. Nous vous conseillons de plus d'inclure le nom de toutes les gares intermédiaires, afin de faciliter le déboguage.
Par exemple, pour le chemin ECBDF donné en exemple à la §2.3.2, la méthode toString doit au moins retourner la chaîne suivante :
Lucerne - Fribourg (13)
mais nous vous suggérons de faire en sorte qu'elle retourne la chaîne :
Lucerne - Berne - Neuchâtel - Soleure - Berne - Fribourg (13)
Vous êtes libres de choisir la représentation textuelle du chemin vide retourné par la méthode longest appliquée à une liste de routes vide, mais faites bien attention à ce qu'aucune exception ne soit levée lorsqu'on lui applique la méthode toString.
3.5.1. Conseils de programmation
Dans la méthode longest, pour déterminer si une route donnée appartient déjà à un chemin à prolonger, vous pouvez soit :
- utiliser la méthode
containsdeList, qui retourne vrai ssi l'objet qu'on lui passe se trouve dans le récepteur (this), - utiliser la méthode
removeAlldeList, qui supprime du récepteur (this) tous les éléments de la collection qu'on lui passe en argument, ce qui vous permet de calculer l'ensemble des routes encore inutilisées.
La seconde solution est un peu plus efficace, mais aussi plus difficile à mettre en œuvre.
3.6. Tests
À partir de cette étape, nous ne vous fournissons plus de tests unitaires, et il vous faut donc les écrire vous-même.
Nous vous fournissons néanmoins une archive Zip à importer dans votre projet et contenant un fichier nommé SignatureChecks_2.java. La classe qu'il contient fait référence à la totalité des classes et méthodes de cette étape, ce qui vous permet de vérifier que leurs noms et types sont corrects. Cela est capital, car la moindre faute à ce niveau empêcherait l'exécution de nos tests unitaires.
Attention : après avoir importé le contenu de cette archive, n'oubliez surtout pas de marquer le répertoire sigcheck comme Sources Root si vous utilisez IntelliJ (voir le point 7 de notre guide), ou de l'ajouter au Java Build Path de votre projet si vous utilisez Eclipse (voir points 5 à 7 de notre guide).
Si vous oubliez de faire cette manipulation, les éventuelles erreurs contenues dans le fichier de vérification de signatures ne seront pas signalées, le rendant ainsi inutile.
Nous vous fournirons de tels fichiers pour toutes les étapes jusqu'à la sixième (incluse), et il vous faudra penser à vérifier systématiquement qu'aucune erreur n'est signalée à leur sujet. Faute de cela, votre rendu pourrait se voir refusé par notre système.
4. Résumé
Pour cette étape, vous devez :
- écrire les classes
RouteetTrailselon les indications données ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 5 mars 2021 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 20 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !
Notes de bas de page
On peut se demander pourquoi nous avons choisi d'identifier les gares au moyen d'entiers, mais les routes au moyen de chaînes de caractères. La raison en est que ces deux identités sont utilisées différemment dans les étapes ultérieures, et notre choix a été guidé par ces utilisations.
Il serait probablement plus propre de lever une autre exception que IllegalArgumentException lorsque la route à laquelle on applique cette méthode n'est pas un tunnel, mais dans un soucis de simplicité, nous avons décidé de lever systématiquement IllegalArgumentException dans ce projet.