Éléments de jeu

Comme cela a été expliqué dans l'introduction au projet, une partie de tCHu se joue sur une carte de la Suisse et des pays voisins, visible ci-dessous¹.

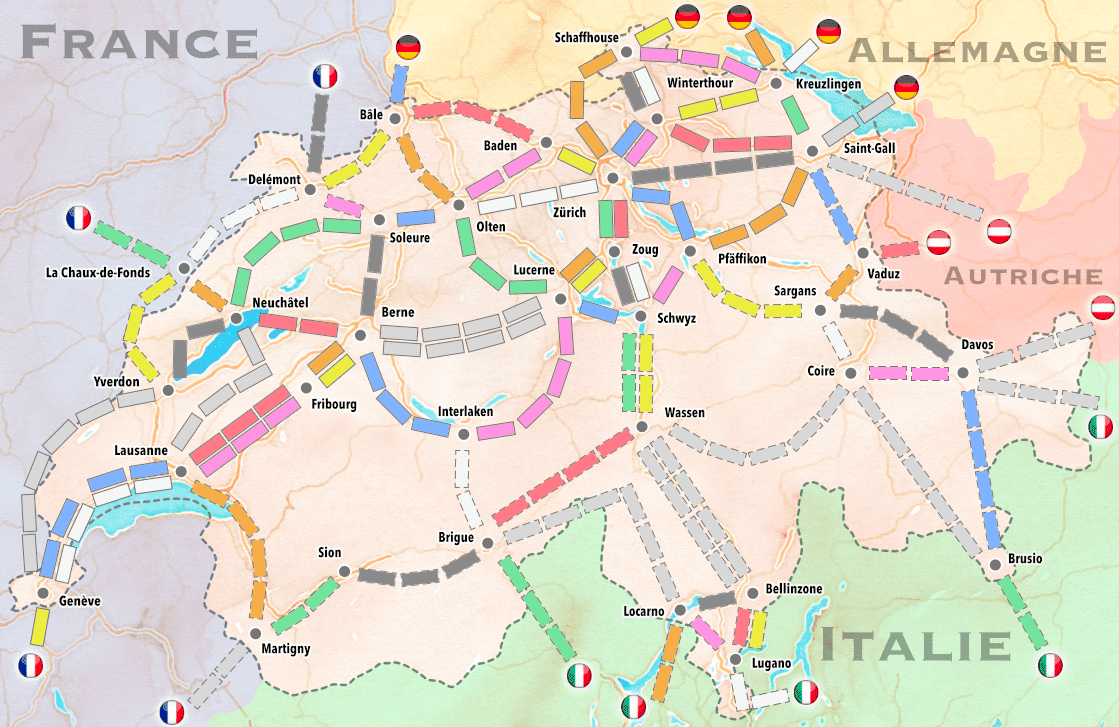
Un certain nombre de villes, toutes suisses, sont nommées sur cette carte. Elles sont reliées entre elles par un réseau ferroviaire représenté par des cases rectangulaires colorées placées les unes derrière les autres. Ce réseau s'étend également aux pays voisins — Allemagne, Autriche, Italie et France — mais les villes des pays voisins ne sont pas nommées et sont simplement représentées par un drapeau du pays.

Une gare (station en anglais) est un point du réseau ferroviaire de tCHu. Il en existe de deux types : celles qui correspondent à des villes suisses, et celles qui correspondent à des villes non spécifiées dans un pays voisin.

La principale caractéristique d'une gare est son nom. Pour celles situées en Suisse, ce nom est simplement celui de leur ville. Pour celles situées dans un pays voisin, ce nom est celui du pays en question. Ainsi, les quatre gares situées en France portent toutes le nom de « France », mais il s'agit néanmoins de gares différentes.

La carte de tCHu comporte 34 gares en Suisse, et 17 dans les pays voisins : 5 en Allemagne, 3 en Autriche, 5 en Italie et 4 en France. Il y a donc 51 gares au total.

Les joueurs de tCHu ont en main en certain nombre de cartes wagon (car cards) et de cartes locomotive (locomotive cards), qu'ils utilisent pour s'emparer des routes du réseau ferroviaire, comme nous le verrons à l'étape suivante.

Les cartes wagon sont ornées d'un dessin de wagon et colorées d'une des huit couleurs utilisées dans le jeu, à savoir : noir, violet, bleu, vert, jaune, orange, rouge, ou blanc. Chaque carte wagon d'une couleur donnée existe en 12 exemplaires, et le jeu comporte donc un total de 96 (8×12) cartes wagon.

Les cartes locomotive sont ornées d'un dessin de locomotive. Bien que ces cartes soient aussi colorées (en turquoise), leur couleur est purement décorative et ne joue aucun rôle dans le jeu, contrairement à celle des cartes wagon. Le jeu comporte 14 cartes locomotive.

Au total, le jeu comporte donc 110 (96+14) cartes wagon et locomotive, que nous appellerons désormais simplement « les cartes ».

En plus des cartes, les joueurs ont également en main un certain nombre de billets (tickets) représentant chacun un objectif à réaliser. Tout comme un billet de train réel, un billet de tCHu est constitué d'un point de départ (p.ex. Lausanne) et d'un point d'arrivée (p.ex. Saint-Gall). De plus, un billet de tCHu vaut un certain nombre de points, qui sont ceux que le joueur qui le possède gagnera (resp. perdra) à la fin de la partie s'il a réussi (resp. échoué) à relier le point de départ au point d'arrivée avec ses propres wagons.

Il existe de trois types de billets tCHu, décrits en détail plus bas :

1. ville à ville,
2. ville à pays,
3. pays à pays.

Le jeu de tCHu comporte un total de 46 billets : 34 billets ville à ville, 4 billets ville à pays, et 8 billets pays à pays. Les billets pays à pays existent en deux exemplaires chacun, tandis que tous les autres billets sont uniques.

Avant de commencer à programmer, il faut vous assurer que la version 11 de Java est bien installée sur votre ordinateur, car c'est celle qui sera utilisée pour ce projet.

Si vous n'avez pas encore installé cette version, rendez-vous sur le site Web du projet AdoptOpenJDK, téléchargez le programme d'installation correspondant à votre système d'exploitation (macOS, Linux ou Windows), et exécutez-le. Ensuite, si vous utilisez Eclipse plutôt qu'IntelliJ, lisez le guide Configurer Eclipse et suivez les indications qui s'y trouvent.

Fréquemment, les méthodes d'un programme demandent que leurs arguments satisfassent certaines conditions. Par exemple, une méthode déterminant la valeur maximale d'un tableau d'entiers exige que ce tableau contienne au moins un élément.

De telles conditions sont souvent appelées préconditions (preconditions) car elles doivent être satisfaites avant l'appel d'une méthode : c'est à l'appelant de s'assurer qu'il n'appelle la méthode qu'avec des arguments valides.

En Java, la convention veut que chaque méthode vérifie, autant que possible, ses préconditions et lève une exception — souvent IllegalArgumentException — si l'une d'entre elles n'est pas satisfaite. Par exemple, une méthode max calculant la valeur maximale d'un tableau d'entiers, et exigeant logiquement que celui-ci contienne au moins un élément, pourrait commencer ainsi :

int max(int[] array) {
  if (! (array.length > 0))
    throw new IllegalArgumentException();
  // … reste du code
}

(Notez au passage que la méthode max ne déclare pas qu'elle lève potentiellement IllegalArgumentException au moyen d'une clause throws, car cette exception est de type unchecked.)

La première classe à réaliser dans le cadre de ce projet a pour but de faciliter l'écriture de telles préconditions. En l'utilisant, la méthode ci-dessus pourrait être simplifiée ainsi :

int max(int[] array) {
  Preconditions.checkArgument(array.length > 0);
  // … reste du code
}

Cette classe est nommée Preconditions et appartient au paquetage ch.epfl.tchu. Elle est publique et finale et n'offre rien d'autre que la méthode checkArgument décrite plus bas. Elle a toutefois la particularité d'avoir un constructeur par défaut privé :

public final class Preconditions {
  private Preconditions() {}
  // … méthodes
}

Le but de ce constructeur privé est de rendre impossible la création d'instances de la classe, puisque cela n'a clairement aucun sens — elle ne sert que de conteneur à une méthode statique. Dans la suite du projet, nous définirons plusieurs autres classes du même type, que nous appellerons dès maintenant classes non instanciables.

La méthode publique (et statique) offerte par la classe Preconditions est :

• void checkArgument(boolean shouldBeTrue), qui lève l'exception IllegalArgumentException si son argument est faux, et ne fait rien sinon.

Le type énuméré Color du paquetage ch.epfl.tchu.game, public, représente les huit couleurs utilisées dans le jeu pour colorer les cartes wagon et les routes. Les valeurs de ce type énuméré sont, dans l'ordre :

1. BLACK (noir),
2. VIOLET (violet)
3. BLUE (bleu),
4. GREEN (vert),
5. YELLOW (jaune),
6. ORANGE (orange),
7. RED (rouge),
8. WHITE (blanc).

En plus de ces valeurs, le type énuméré Color offre deux attributs publics, statiques et finaux, qui sont :

• List<Color> ALL, une liste immuable contenant la totalité des valeurs du type énuméré, dans leur ordre de définition (voir les conseils de programmation ci-dessous),
• int COUNT, qui contient le nombre de valeurs du type énuméré.

Le type énuméré Card du paquetage ch.epfl.tchu.game, public, représente les différents types de cartes du jeu, à savoir les huit types de cartes wagon (un par couleur), et le type de carte locomotive.

Les éléments de ce type énuméré sont, dans l'ordre :

1. BLACK (wagon noir),
2. VIOLET (wagon violet),
3. BLUE (wagon bleu),
4. GREEN (wagon vert),
5. YELLOW (wagon jaune),
6. ORANGE (wagon orange),
7. RED (wagon rouge),
8. WHITE (wagon blanc),
9. LOCOMOTIVE (locomotive).

En plus de ces valeurs, Card offre les attributs ALL et COUNT, définis de la même manière que dans Color, ainsi que l'attribut public, final et statique suivant :

• List<Card> CARS, qui contient uniquement les cartes wagon, dans l'ordre de définition, c-à-d de BLACK à WHITE.

En dehors des attributs, le type énuméré Card offre la méthode publique et statique suivante :

• Card of(Color color), qui retourne le type de carte wagon correspondant à la couleur donnée.

Finalement, le type énuméré Card offre la méthode publique suivante :

• Color color(), qui retourne la couleur du type de carte auquel on l'applique s'il s'agit d'un type wagon, ou null s'il s'agit du type locomotive.

La classe Station du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente une gare. Elle offre un unique constructeur public :

• Station(int id, String name), qui construit une gare ayant le numéro d'identification et le nom donnés, ou lève IllegalArgumentException si le numéro d'identification est strictement négatif (< 0).

Le numéro d'identification d'une gare est un numéro unique compris entre 0 et le nombre de gares du réseau moins un. Par exemple, étant donné que le réseau de tCHu comporte 51 gares, elles seront identifiées par un numéro allant de 0 à 50. La valeur exacte du numéro d'identification importe peu, la seule chose qui compte est que chaque gare ait son propre numéro. L'utilité de ce numéro deviendra claire à l'étape 4.

Il faut noter que, comme nous l'avons vu à la §2.2, les gares qui se trouvent dans un pays voisin de la Suisse portent le nom de leur pays. Il est donc tout à fait possible que plusieurs gares différentes portent le même nom, mais elles doivent néanmoins avoir chacune un numéro d'identification différent.

En plus du constructeur, la classe Station offre deux méthodes publiques qui donnent accès aux deux attributs de la gare, à savoir :

• int id(), qui retourne le numéro d'identification de la gare,
• String name(), qui retourne le nom de la gare.

Finalement, la classe Station redéfinit la méthode toString pour qu'elle retourne le nom de la gare.

L'interface StationConnectivity du paquetage ch.epfl.tchu.game, publique, représente ce que nous appellerons la « connectivité » du réseau d'un joueur, c-à-d le fait que deux gares du réseau de tCHu soient reliées ou non par le réseau du joueur en question.

Cette interface n'offre qu'une seule méthode, publique et abstraite, qui est :

• boolean connected(Station s1, Station s2), qui retourne vrai si et seulement si les gares données sont reliées par le réseau du joueur.

Un exemple simple mais peu réaliste d'une classe implémentant cette interface est :

public class FullConnectivity implements StationConnectivity {
  @Override
  public boolean connected(Station s1, Station s2) {
    return true;
  }
}

Cette classe considère que n'importe quelle gare est connectée à n'importe quelle autre, puisque sa méthode connected retourne toujours vrai ! Elle correspond donc au réseau d'un joueur qui aurait réussi à connecter toutes les gares du réseau de tCHu entre elles, ce qui n'est probablement pas possible.

Bien entendu, la classe implémentant StationConnectivity que nous utiliserons dans le projet sera plus sophistiquée — et plus utile — que cela. Elle sera en effet capable de déterminer s'il est possible d'aller d'une gare quelconque du réseau à une autre en empruntant uniquement des routes appartenant à un joueur donné. Grâce à cette classe, il sera possible de déterminer les objectifs qui auront été atteints par les différents joueurs, et de calculer ainsi les points qu'ils méritent.

Cette classe plus sophistiquée est toutefois trop complexe pour être écrite dans le cadre de cette étape, et nous ne l'écrirons qu'à l'étape 4. Grâce à l'existence de l'interface StationConnectivity ci-dessus, il nous est toutefois déjà possible d'écrire du code ayant besoin de cette classe sans qu'elle existe pour autant. Ce code est bien entendu celui déterminant le nombre de points que rapportent les billets, qui est réparti entre les classes Trip et Ticket décrites ci-après.

La classe Trip du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente ce que nous avons appelé un trajet. Elle offre un unique constructeur public :

• Trip(Station from, Station to, int points), qui construit un nouveau trajet entre les deux gares données et valant le nombre de points donné, ou lève NullPointerException si l'une des deux gares est nulle et IllegalArgumentException si le nombre de points n'est pas strictement positif (> 0).

En plus de ce constructeur, la classe Trip offre une méthode publique et statique :

• List<Trip> all(List<Station> from, List<Station> to, int points), qui retourne la liste de tous les trajets possibles allant d'une des gares de la première liste (from) à l'une des gares de la seconde liste (to), chacun valant le nombre de points donné ; lève IllegalArgumentException si l'une des listes est vide, ou si le nombre de points n'est pas strictement positif.

Finalement, la classe Trip offre les méthodes publiques suivantes :

• Station from(), qui retourne la gare de départ du trajet,
• Station to(), qui retourne la gare d'arrivée du trajet,
• int points(), qui retourne le nombre de points du trajet,
• int points(StationConnectivity connectivity), qui retourne le nombre de points du trajet pour la connectivité donnée.

La seconde variante de la méthode points retourne le nombre de points du trajet si la méthode connected de la connectivité qu'on lui passe retourne vrai lorsqu'on l'applique aux deux gares du trajet — ce qui signifie qu'elles sont bien connectées —, et la négation de ce nombre de points sinon.

La classe Ticket du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente un billet. Pour des raisons qui deviendront claires plus tard, cette classe implémente l'interface Comparable<Ticket> et sa définition ressemble donc à ceci :

public final class Ticket implements Comparable<Ticket> {
  // … corps de la classe
}

Pour l'instant, il n'est pas nécessaire de comprendre pourquoi la classe Ticket implémente cette interface. Il suffit de savoir que cela implique qu'elle doit offrir une méthode de comparaison nommée compareTo, décrite plus bas.

La classe Ticket offre les deux constructeurs suivants :

• Ticket(List<Trip> trips), qui construit un billet constitué de la liste de trajets donnée, ou lève IllegalArgumentException si celle-ci est vide, ou si toutes les gares de départ des trajets n'ont pas le même nom,
• Ticket(Station from, Station to, int points), qui construit un billet constitué d'un unique trajet, dont les attributs sont from, to et points.

Notez que le premier de ces constructeurs est ce que nous nommerons le constructeur principal, et c'est lui qui se charge d'initialiser les attributs de la classe. Le second constructeur est quant à lui ce que nous nommerons un constructeur secondaire, ce qui signifie qu'il consiste en un simple appel au constructeur principal, qui se fait au moyen de la notation this(…).

En plus de ces constructeurs, la classe Ticket offre les méthodes publiques suivantes, au sujet desquels des conseils de programmation vous sont donnés plus bas :

• String text(), qui retourne la représentation textuelle du billet, telle que décrite à la §2.4.5,
• int points(StationConnectivity connectivity), qui retourne le nombre de points que vaut le billet, sachant que la connectivité donnée est celle du joueur possédant le billet,
• int compareTo(Ticket that), qui compare le billet auquel on l'applique (this) à celui passé en argument (that) par ordre alphabétique de leur représentation textuelle, et retourne un entier strictement négatif si this est strictement plus petit que that, un entier strictement positif si this est strictement plus grand que that, et zéro si les deux sont égaux.

De plus, la classe Ticket redéfinit la méthode toString de Object afin qu'elle retourne la même valeur que la méthode text.

Pour vous aider à démarrer ce projet, nous vous fournissons exceptionnellement une archive Zip contenant des tests unitaires JUnit pour cette étape.

Pour pouvoir utiliser ces tests, il vous faut :

1. les importer dans votre projet (instructions pour IntelliJ ou Eclipse),
2. ajouter la bibliothèque JUnit à votre projet (instructions pour IntelliJ ou Eclipse).

Une fois les tests exécutés avec succès, il vous reste à documenter la totalité des entités publiques (classes, attributs et méthodes) définies dans cette étape, au moyen de commentaires Javadoc, comme décrit dans le guide consacré à ce sujet. Vous pouvez écrire ces commentaires en français ou en anglais, en fonction de votre préférence, mais vous ne devez utiliser qu'une seule langue pour tout le projet.