Dessin du ciel
Rigel – étape 8
1 Introduction
Le but de cette étape est d'écrire une classe permettant de dessiner le ciel et de pouvoir ainsi enfin générer des images.
2 Concepts
2.1 Représentation des objets célestes
La totalité des objets célestes gérés par ce projet (étoiles, planètes, Soleil et Lune) ont l'apparence d'un disque quand on les observe depuis la Terre. Il paraît donc raisonnable de les représenter par des disques à l'écran. La question se pose toutefois de savoir quelle taille et quelle couleur doivent avoir ces disques.
2.2 Taille des objets
Pour la taille, la solution la plus évidente est de la déterminer en fonction de la taille angulaire de l'objet. Malheureusement, à l'exception de la Lune et du Soleil, tous les objets célestes ont une taille angulaire tellement petite qu'ils apparaissent comme de simples points lumineux à l'œil nu ou à la jumelle.1
Il importe donc de trouver une autre solution pour déterminer la taille des disques représentant les étoiles et les planètes. Une idée assez naturelle consiste à utiliser pour cela la magnitude de ces objets. En effet, plus un objet est brillant et plus il semble important aux yeux d'un observateur, et il paraît donc raisonnable de dimensionner le disque le représentant en fonction.
Nous adopterons donc la stratégie hybride suivante pour déterminer la taille du disque représentant un objet céleste donné :
- s'il s'agit du Soleil ou de la Lune, le disque a la taille du disque effectivement visible depuis la Terre,
- s'il s'agit d'une planète ou d'une étoile, le disque a une taille proportionnelle à la magnitude de l'objet — en réalité, inversement proportionnelle car plus la magnitude est grande, moins l'objet est brillant.
Ces deux cas sont détaillés ci-après.
2.2.1 Taille effective
Nous avons vu à la §2.1.5 de l'étape 4 que la projection stéréographique que nous utilisons projette un objet de taille angulaire θ en un disque dont le diamètre est :
\[ d = 2\tan\left(\frac{\theta}{4}\right) \]
Comme nous l'avions mentionné alors, cette équation n'est correcte que pour un objet situé au centre de projection, mais nous l'utiliserons néanmoins systématiquement, indépendamment de la position des objets considérés.
Par exemple, vu depuis la Terre, le Soleil a une taille angulaire qui ne varie pas beaucoup et vaut environ un demi degré. Dès lors, nous le représenterons par un disque dont le diamètre vaut approximativement :
\[ 2\tan\left(\frac{0.5°}{4}\right) \approx 4.36\times10^{-3} \]
Le fait que ce diamètre soit aussi petit peu surprendre mais est simplement dû au fait que la sphère céleste — qui est la sphère projetée ici — a un diamètre quelconque, et celui-ci a été fixé à 1 unité pour simplifier les formules de projection. Une conséquence de ce choix est que la plupart du ciel est projetée dans une très petite zone autour de l'origine, ce qui explique la petitesse du diamètre du disque solaire.
Le diamètre à l'écran du disque solaire devra donc être calculé en fonction du diamètre ci-dessus, en appliquant une importante dilatation décrite à la §2.6 ci-dessous.
2.2.2 Taille basée sur la magnitude
La taille des disques représentant les étoiles et les planètes sera calculée en fonction de leur magnitude. Il reste encore à décider comment effectuer ce calcul.
Pour commencer, il faut noter qu'aucun des objets dont la taille est déterminée en fonction de sa magnitude ne devrait être plus gros que le Soleil ou la Lune, car cela serait visuellement troublant. Dès lors, il paraît raisonnable de décider que le plus gros de ces objets devrait avoir un diamètre égal à 95% de celui d'un objet dont la taille angulaire est d'un demi degré — comme le Soleil ou la Lune.
D'autre part, il faudrait aussi éviter qu'un objet ait une taille nulle, faute de quoi il serait totalement invisible. Dès lors, il paraît aussi raisonnable de décider que le plus petit de ces objets devrait avoir un diamètre égal à 10% de celui d'un objet dont la taille angulaire est d'un demi degré.
Finalement, comme la plupart des planètes et étoiles visibles ont une magnitude comprise dans l'intervalle [-2, 5], il paraît raisonnable d'écrêter leur magnitude réelle à cet intervalle.
En combinant ces trois observations, on peut déduire la technique suivante de calcul de la taille du disque représentant un objet céleste en fonction de sa magnitude :
- sa magnitude est écrêtée à l'intervalle [-2, 5],
- en fonction de cette magnitude écrêtée, un facteur de taille est calculé de telle manière à ce que la magnitude -2 produise un facteur de 0.95 et la magnitude 5 un facteur de 0.10,
- le diamètre qu'aurait un objet de taille apparente de 0.5° est multiplié par ce facteur pour obtenir le diamètre de l'objet.
Les formules ci-dessous résument ces calculs, où \(m\) est la magnitude réelle de l'objet, \(m^\prime\) la magnitude écrêtée, \(f\) le facteur de taille et \(d\) le diamètre de l'objet :
\begin{align*} m^\prime &= \begin{cases} -2 & \text{si \(m \le -2\)}\\[0.2em] 5 & \text{si \(m \ge 5\)}\\[0.2em] m & \text{sinon}\\[0.2em] \end{cases}\\[0.5em] f &= \frac{99 - 17\,m^\prime}{140}\\[0.5em] d &= f\cdot 2\tan\left(\frac{0.5°}{4}\right) \end{align*}Par exemple, pour un objet de magnitude 0.18 (Rigel), on obtient :
\begin{align*} m^\prime &= 0.18\\ f &\approx 0.685\\ d &\approx 2.99\times 10^{-3} \end{align*}2.3 Couleur des objets
Pour la plupart des objets, la couleur du disque les représentant s'impose naturellement, comme la table suivante l'illustre :
| Objet | Couleur |
|---|---|
| étoile | selon la température de couleur |
| planète | gris clair (voir ci-dessous) |
| Soleil | jaune et blanc (voir §3.3) |
| Lune | blanc |
Il aurait été possible, et peut-être préférable, de choisir une couleur plus réaliste pour les planètes. Par exemple, Mars est rouge, ce qui est perceptible à l'œil nu dans de bonnes conditions d'observations. Nous n'avons toutefois aucune information sur la couleur des planètes dans ce projet, raison pour laquelle un gris clair a été choisi.
2.4 Annotations
En plus des disques représentant les objets célestes, la représentation du ciel est augmentée de deux annotations :
- les figures des astérismes, en bleu,
- l'horizon et les points cardinaux et intercardinaux, en rouge.
L'horizon n'est rien d'autre que la projection (stéréographique) du parallèle de latitude 0°. Pour mémoire, la projection stéréographique d'un parallèle est toujours un cercle.
2.5 Ordre de dessin
Il est possible que les différents éléments présents dans le dessin du ciel — objets célestes et annotations — se chevauchent. Dès lors, il faut choisir l'ordre dans lequel dessiner ces informations, car cela détermine quelle information se trouve devant l'autre lors d'un chevauchement.
2.5.1 Objets célestes
Les objets célestes doivent naturellement être dessinés du plus éloigné au plus proche de la Terre, donc dans l'ordre suivant :
- étoiles,
- planètes,
- Soleil,
- Lune.
Un problème se pose toutefois avec les planètes inférieures — Mercure et Vénus — qui, observées depuis la Terre, peuvent être soit devant soit derrière le Soleil.
Nous ignorerons toutefois ce détail et dessinerons toujours le Soleil devant les planètes, car le passage d'une planète devant le Soleil — nommé transit — n'est observable qu'au moyen d'un télescope équipé de filtres, comme l'illustre l'image ci-dessous.

2.5.2 Annotations
Les figures des astérismes sont dessinées en tout premier, avant les étoiles, afin de ne pas les masquer.
L'horizon et les points cardinaux et intercardinaux sont quant à eux dessinés en tout dernier, afin de ne jamais être masqués par quoi que ce soit.
2.6 Changement de repère
La projection stéréographique que nous utilisons projette les coordonnées horizontales dans le plan. L'échelle à laquelle cette projection est faite a été choisie, comme nous l'avons vu, de manière à simplifier les formules de projection.
Dès lors, après projection, les objets sont correctement placés les uns par rapport aux autres, mais leurs coordonnées exactes sont arbitraires, comme l'exemple de la §2.2.1 l'a illustré. Il est donc clair que ces coordonnées devront être ajustées d'une manière ou d'une autre avant d'être utilisées pour afficher les objets à l'écran.
De plus, la projection stéréographique place les objets de manière à ce que le centre de projection se trouve à l'origine du plan, c-à-d au point de coordonnées (0, 0). Or en informatique, l'origine du repère utilisé pour les images se situe dans le coin haut-gauche de l'image.
Finalement, l'axe des ordonnées du plan pointe vers le haut, alors qu'en informatique, le repère utilisé pour les images a un axe des ordonnées qui pointe vers le bas.
Ces conventions sont illustrées à la figure ci-dessous, qui montre les repères utilisés par la projection stéréographique (en rouge) et par les images en informatique (en bleu). L'image elle-même est représentée par le rectangle blanc.
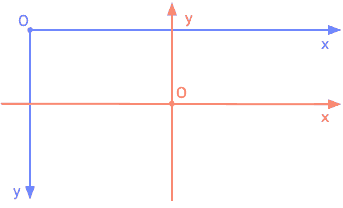
En raison de ces différences entre les deux repères, les coordonnées produites par la projection stéréographique doivent être transformées une dernière fois pour obtenir les coordonnées de l'image. Cette transformation peut se faire en composant :
- une dilatation, dont le but est d'une part d'effectuer la mise à l'échelle de l'image et d'autre part d'inverser le sens des ordonnées,
- une translation, dont le but est de déplacer l'origine.
Par exemple, imaginons que l'image ait une taille de 800×600 pixels, ce qui implique que les coordonnées des points qu'elle contient vont de 0 à 799 pour les abscisses, et de 0 à 599 pour les ordonnées. Admettons de plus que le facteur de mise à l'échelle soit de 1300 — la manière dont ce facteur est calculé sera expliquée dans une étape ultérieure. Dans ce cas, le facteur de dilatation est de 1300 pour les abscisses, de -1300 pour les ordonnées (afin d'inverser leur sens) et la translation est de 400 pour les abscisses et 300 pour les ordonnées.
3 Mise en œuvre Java
La mise en œuvre de cette étape se fera dans une seule classe. Avant de la décrire, il faut toutefois dire quelques mots des classes JavaFX nécessaires à sa réalisation.
3.1 Canevas JavaFX
La classe Canvas de JavaFX représente un canevas, c-à-d une zone rectangulaire sur laquelle il est possible de dessiner différentes formes géométriques de base — traits, cercles, etc. Le dessin du ciel se fera sur un tel canevas.
Pour comprendre comment l'utiliser, il vous faut lire la documentation des deux classes suivantes :
Canvas, qui représente le canevas lui-même, mais qui est extrêmement simple car le dessin sur le canevas se fait au travers de son « contexte graphique »,GraphicsContext, qui représente le contexte graphique associé à un canevas et offre un grand nombre de méthodes permettant de dessiner sur celui-ci.
Le programme d'exemple ci-dessous, qu'il est conseillé d'étudier attentivement, illustre l'utilisation de ces deux classes pour dessiner une approximation du logo de l'EPFL.
public class EpflLogo extends Application {
public static void main(String[] args) { launch(args); }
@Override
public void start(Stage primaryStage) {
Canvas canvas = new Canvas(800, 300);
GraphicsContext ctx = canvas.getGraphicsContext2D();
// Fond blanc
ctx.setFill(Color.WHITE);
ctx.fillRect(0, 0, canvas.getWidth(), canvas.getHeight());
// Texte EPFL rouge
ctx.setFont(Font.font("Helvetica", 300));
ctx.setFill(Color.RED);
ctx.setTextAlign(TextAlignment.CENTER);
ctx.setTextBaseline(VPos.BASELINE);
ctx.fillText("EPFL", 400, 250);
// Trous dans le E et le F
ctx.setFill(Color.WHITE);
ctx.fillRect(50, 126, 30, 26);
ctx.fillRect(450, 126, 30, 26);
primaryStage.setScene(new Scene(new BorderPane(canvas)));
primaryStage.show();
}
}
En l'exécutant, vous devriez voir une fenêtre ressemblant à celle de l'image ci-dessous s'afficher à l'écran.

3.2 Transformations JavaFX
La classe Transform de JavaFX représente une transformation affine et sera utile pour représenter le passage du repère de la projection stéréographique au repère du canevas.
Pour mémoire, ce changement de repère est composé de deux transformations successives : une dilatation et une translation. La méthode scale permet de créer une transformation représentant une dilatation, tandis que la méthode translate permet d'en créer une représentant une translation. Une fois créées, ces deux transformations peuvent être composées au moyen de la méthode createConcatenation.
Une fois la transformation désirée construite, différentes méthodes permettent de transformer différents types de valeurs, comme suit :
- la méthode
transformpermet de transformer un point individuel, - la méthode
deltaTransformpermet de transformer un vecteur individuel, - la méthode
transform2DPointspermet de transformer en une fois plusieurs points stockés dans un tableau.
La différence entre transform et deltaTransform est que cette dernière ignore l'éventuelle translation de la transformation, ce qui est correct pour les vecteurs qui n'ont pas de position.
Notez qu'il est également possible d'effectuer la transformation inverse au moyen des méthodes dont le nom commence par inverse.
3.3 Classe SkyCanvasPainter
La classe SkyCanvasPainter du paquetage ….gui est une classe instanciable représentant un « peintre de ciel », c-à-d un objet capable de dessiner le ciel sur un canevas.
Le canevas à utiliser pour le dessin est passé au constructeur de cette classe, qui offre ensuite des méthodes publiques permettant de dessiner les différents éléments du ciel. Ces méthodes pourraient être :
clear, qui efface le canevas,drawStars, qui dessine les astérismes et les étoiles sur le canevas,drawPlanets, qui dessine les planètes,drawSun, qui dessine le Soleil,drawMoon, qui dessine la Lune,drawHorizon, qui dessine l'horizon et les points cardinaux et intercardinaux.
Avoir une méthode de dessin pour chaque élément permet d'une part d'augmenter la lisibilité du code, et d'autre part de facilement activer ou désactiver le dessin de certains éléments.
La plupart de ces méthodes ont besoin des mêmes informations pour faire le dessin, qui sont : le ciel observé, la projection stéréographique utilisée, et la transformation entre le repère de la projection et celui du canevas.
Les couleurs à utiliser pour dessiner les différents éléments sont :
- pour les étoiles : la couleur obtenue via
BlackBodyColor, - pour les astérismes :
Color.BLUE, - pour les planètes :
Color.LIGHTGRAY, - pour le Soleil : voir ci-dessous,
- pour la Lune :
Color.WHITE, - pour l'horizon et les points intercardinaux :
Color.RED.
Pour le rendre plus facilement identifiable, et pour tenter de représenter sa luminosité extrême, le Soleil est représenté au moyen des trois disques concentriques suivants :
- un disque dont le diamètre est celui du Soleil et la couleur
Color.WHITE, - un disque dont le diamètre est celui du Soleil plus 2 et la couleur
Color.YELLOW, - un disque dont le diamètre est celui du Soleil multiplié par 2.2 et dont la couleur est
Color.YELLOWmais avec une opacité de 25% seulement, représentant un halo autour du Soleil.
Ces trois disques doivent bien entendu être dessinés du plus grand au plus petit.
Les astérismes doivent être dessinés avec un trait de largeur 1. Attention toutefois : aucun trait ne doit être dessiné entre deux étoiles invisibles, c-à-d deux étoiles dont le centre n'est pas dans les limites du canevas.
L'horizon doit être dessiné avec un trait de largeur 2. Les points cardinaux et intercardinaux doivent être nommés selon les conventions françaises (N, NE, E, SE, S, SO, O, NO). Leurs noms doivent être positionnés de manière à être horizontalement centrés sur leur position (p.ex. 180° pour le point S) et afin que le sommet du texte se trouve à la position correspondant à un demi degré en dessous de l'horizon. La police utilisée doit être la police par défaut, donc aucun appel à setFont ne doit être fait.
3.3.1 Conseils de programmation
La meilleure solution pour dessiner les astérismes consiste à construire ce que l'on nomme un chemin (path) pour chacun d'entre eux. Les méthodes beginPath, moveTo, lineTo et stroke de GraphicsContext sont utiles pour cela.
Comme dit plus haut, il ne faut pas dessiner de trait entre deux étoiles qui se trouvent toutes deux hors des limites du canevas. Ces dernières s'obtiennent au moyen de la méthode getBoundsInLocal, et leur méthode contains permet de tester si elles contiennent un point.
Pour obtenir la couleur du halo du Soleil, la méthode deriveColor est utile.
3.4 Tests
Pour tester votre dessin du ciel, vous pouvez utiliser un programme du type de celui donné ci-dessous, qui dessine une image du ciel au sud de l'EPFL le 17 février 2020 à 20h15.
La première partie de ce programme devrait être simple à comprendre, car elle utilise exclusivement des concepts étudiés au cours des étapes précédentes.
Le dessin de l'image est fait sur un canevas de 800×600 pixels. La variable planeToCanvas contient la transformation permettant de passer des coordonnées produites par la projection stéréographique aux coordonnées de l'image. Il s'agit de la composition d'une dilatation d'un facteur 1300 — choisi car il permet d'obtenir une image intéressante — et d'une translation de 400 unités pour les abscisses et de 300 unités pour les ordonnées.
Les dernières lignes créent tout d'abord une image JavaFX au moyen de la méthode snapshot de Canvas, avant de la transformer en une image Swing qui est malheureusement le seul type d'image à partir duquel il est facile d'obtenir un fichier image. Ce fichier est ensuite produit au moyen de la méthode write de ImageIO.
public final class DrawSky extends Application {
public static void main(String[] args) { launch(args); }
private InputStream resourceStream(String resourceName) {
return getClass().getResourceAsStream(resourceName);
}
@Override
public void start(Stage primaryStage) throws Exception {
try (InputStream hs = resourceStream("/hygdata_v3.csv")){
StarCatalogue catalogue = new StarCatalogue.Builder()
.loadFrom(hs, HygDatabaseLoader.INSTANCE)
.build();
ZonedDateTime when =
ZonedDateTime.parse("2020-02-17T20:15:00+01:00");
GeographicCoordinates where =
GeographicCoordinates.ofDeg(6.57, 46.52);
HorizontalCoordinates projCenter =
HorizontalCoordinates.ofDeg(180, 45);
StereographicProjection projection =
new StereographicProjection(projCenter);
ObservedSky sky =
new ObservedSky(when, where, projection, catalogue);
Canvas canvas =
new Canvas(800, 600);
Transform planeToCanvas =
Transform.affine(1300, 0, 0, -1300, 400, 300);
SkyCanvasPainter painter =
new SkyCanvasPainter(canvas);
painter.clear();
painter.drawStars(sky, projection, planeToCanvas);
WritableImage fxImage =
canvas.snapshot(null, null);
BufferedImage swingImage =
SwingFXUtils.fromFXImage(fxImage, null);
ImageIO.write(swingImage, "png", new File("sky.png"));
}
Platform.exit();
}
}
Après avoir exécuté ce programme, un fichier nommé sky.png devrait se trouver dans le répertoire de votre projet. En l'ouvrant, vous devriez voir l'image ci-dessous, dont la taille a été réduite pour des questions de présentation — un clic permet de la voir en taille réelle :

Orion est bien visible au centre de cette image, et l'amas des Pléiades se devine en haut à droite.
4 Résumé
Pour cette étape, vous devez :
- écrire la classe
SkyCanvasPainterselon les instructions données plus haut, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies.
Aucun rendu n'est à faire pour cette étape avant le rendu final. N'oubliez pas de faire régulièrement des copies de sauvegarde de votre travail en suivant nos indications à ce sujet.
Notes de bas de page
Il va sans dire qu'il ne faut jamais observer le Soleil à l'œil nu ou à la jumelle.