Projection et objets célestes
Rigel – étape 4
1 Introduction
Le but de cette quatrième étape est double : d'une part, écrire le code permettant de projeter les coordonnées sphériques afin de pouvoir placer les différents objets célestes à l'écran ; et d'autre part, écrire les classes représentant certains de ces objets célestes : planètes, Lune et Soleil.
2 Concepts
2.1 Projection stéréographique
Tous les systèmes de coordonnées décrits jusqu'à présent sont sphériques. Or notre but final est de dessiner le ciel sur un plan : l'écran de l'ordinateur. Il nous faut donc décider comment transformer les coordonnées horizontales d'un objet céleste en coordonnées du plan (cartésiennes).
Ce problème est similaire à celui auquel font face les cartographes, qui désirent représenter sur une carte (plane) la surface de la Terre (sphérique). Ils ont dans ce but inventé un grand nombre de projections cartographiques — un exemple étant la célèbre projection de Mercator, souvent utilisée pour les cartes représentant le monde entier.
Si la projection de Mercator convient relativement bien pour de telles cartes, elle ne convient pas du tout pour une carte du ciel, car elle déforme énormément les régions polaires. Dans le cas de la Terre, cela n'est pas très grave, ces zones n'étant que très peu peuplées. Par contre, dans le cas du ciel, cela est inacceptable car les régions polaires — en particulier le zénith — sont « peuplées » de nombreux objets célestes intéressants.
Dès lors, le choix d'une autre projection s'impose, et c'est la projection dite stéréographique qui est généralement utilisée en astronomie. Cette projection est paramétrée par un point central, qui est le point projeté à l'origine du plan. Par exemple, la figure 1 ci-dessous montre une projection stéréographique de la Terre centrée sur le Pôle Nord.
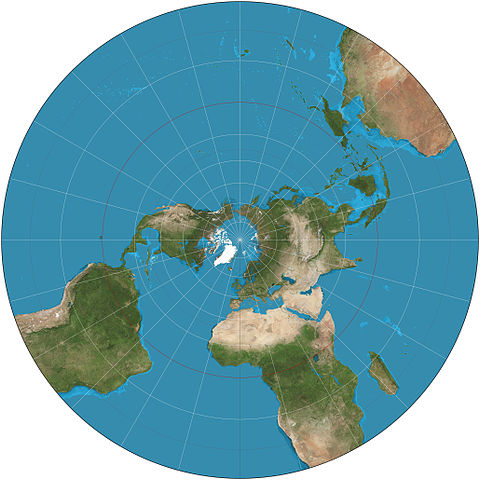
La projection stéréographique peut s'utiliser pour projeter n'importe quel système de coordonnées sphériques, p.ex. les coordonnées géographiques comme dans l'exemple ci-dessus. Dans ce projet, nous ne l'utiliserons toutefois que pour projeter la position des objets célestes visibles dans le ciel, et les coordonnées à projeter seront donc dans le système horizontal.
Cela dit, les formules ci-dessous utilisent les variables communément utilisées pour désigner la longitude et la latitude dans un système sphérique quelconque, à savoir λ et ϕ, plutôt que celles spécifiques au système horizontal.
2.1.1 Projection d'un point
La projection stéréographique centrée en \((\lambda_0, \phi_1)\) projette le point de coordonnées sphériques \((\lambda, \phi)\) en le point du plan de coordonnées cartésiennes \((x,y)\) de la manière suivante :
\begin{align*} x &= d\,\cos\phi\,\sin\lambda_\Delta\\[0.5em] y &= d\,\left(\sin\phi\,\cos\phi_1 - \cos\phi\,\sin\phi_1\,\cos\lambda_\Delta\right) \end{align*}où
\begin{align*} d &= \frac{1}{1 + \sin\phi\,\sin\phi_1 + \cos\phi\,\cos\phi_1\,\cos\lambda_\Delta}\\[0.5em] \lambda_\Delta &= \lambda - \lambda_0 \end{align*}2.1.2 Inversion de la projection d'un point
Comme toutes les projections cartographiques, la projection stéréographique peut être inversée, c-à-d qu'il est possible d'obtenir les coordonnées sphériques correspondant aux coordonnées cartésiennes d'un point. Les formules sont les suivantes :
\begin{align*} \lambda &= \arctan\left[\frac{x\,\sin c}{\rho\,\cos\phi_1\,\cos c - y\,\sin\phi_1\,\sin c}\right] + \lambda_0\\[0.5em] \phi &= \arcsin\left[\cos c\,\sin\phi_1 + \frac{y\,\sin c\,\cos\phi_1}{\rho}\right]\\ \end{align*}où
\begin{align*} \rho &= \sqrt{x^2 + y^2}\\[0.5em] \sin c &= \frac{2\rho}{\rho^2 + 1}\\[0.5em] \cos c &= \frac{1 - \rho^2}{\rho^2 + 1} \end{align*}Dans ces formules, la variable c correspond bien à un angle, mais comme seuls son sinus et son cosinus sont utiles, et que ceux-ci sont calculables directement — sans recours à des fonctions trigonométriques —, aucune formule de calcul de c n'est nécessaire.
2.1.3 Projection d'un parallèle
Pour mémoire, un parallèle est une ligne de latitude constante, et plusieurs d'entre eux sont visibles sur l'image de la figure 1 ci-dessus, sur laquelle ils forment des cercles concentriques centrés sur le Pôle Nord — l'équateur étant indiqué en rouge. Notez toutefois que ces cercles ne seraient plus concentriques si la projection n'était pas centrée sur un pôle.
La projection stéréographique a la particularité de projeter les parallèles en des cercles du plan. Ainsi, le parallèle de latitude \(\phi\) est projeté en un cercle centré en \((c_x, c_y)\) et de rayon \(\rho\), dont les valeurs sont données par les formules suivantes :
\begin{align*} (c_x, c_y) &= \left(0, \frac{\cos\phi_1}{\sin\phi + \sin\phi_1}\right)\\[0.5em] \rho &= \frac{\cos\phi}{\sin\phi + \sin\phi_1} \end{align*}Notez que si la latitude du centre de projection et celle du parallèle valent toutes deux 0, alors aussi bien l'ordonnée du centre du cercle que son rayon valent \(\tfrac{1}{0} = \infty\). Dans ce cas, le « cercle » est donc une simple droite (voir l'équateur dans la figure 2).
2.1.4 Projection d'un méridien
La projection stéréographique a également la particularité de projeter les méridiens — les lignes de longitude constante — en des cercles du plan. Toutefois, comme nous ne dessinerons pas de méridiens dans le cadre de ce projet, les paramètres de ces cercles ne sont pas donnés ici.
2.1.5 Projection d'un angle
Comme la plupart des projections cartographiques, la projection stéréographique ne préserve pas les aires. Cela signifie par exemple que deux objets identiques placés à différents endroits de la sphère projetée pourront avoir des projections différentes, en particulier d'aire distincte.
Cela est illustré par la figure 2 ci-dessous, qui montre une projection stéréographique de la Terre, centrée cette fois sur l'océan Indien. On y voit ce que l'on nomme des indicatrices de Tissot, qui sont les formes résultant de la projection de cercles identiques placés à intervalles réguliers sur la sphère à projeter, et qui facilitent la visualisation des déformations introduites par la projection.
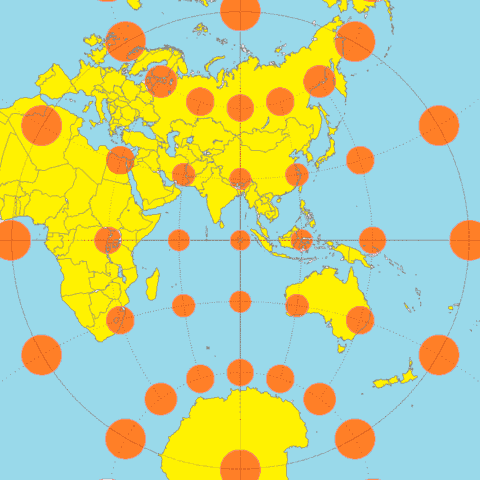
Dans le cas de la projection stéréographique, on constate que les formes résultant de la projection de ces cercles sont toujours des cercles, mais leur taille et leur position relative change en fonction de leur éloignement du centre de projection.
En conséquence, lorsque la projection stéréographique est utilisée pour dessiner le ciel, la représentation des objets célestes de taille perceptible à l'œil nu — à savoir la Lune et le Soleil — devrait normalement varier en fonction de leur position dans le ciel. Il n'est toutefois pas clair que cette variation apporte réellement quelque chose, et dans un souci de simplicité nous représenterons donc toujours la Lune et le Soleil à la taille qu'ils auraient s'ils se trouvaient au centre de la projection, et que celui-ci était à l'horizon. (Cas qui correspond à celui de l'indicatrice de Tissot qui se trouve exactement au centre de l'image de la figure 2.)
Dans une telle situation, le diamètre projeté d d'un objet de taille angulaire θ est donné par la formule suivante :
\[ d = 2\tan\left(\frac{\theta}{4}\right) \]
(La notion de taille angulaire est décrite à la §2.2.2 ci-dessous.)
2.2 Objets célestes
Les objets célestes intéressants à observer en astronomie sont nombreux : étoiles, planètes, satellites (naturels ou artificiels), galaxies, etc. Dans ce projet, nous représenterons uniquement ceux qui sont faciles à observer à l'œil nu, à savoir : la Lune, le Soleil, les planètes du système solaire (Mercure, Vénus, Mars, Jupiter, Saturne, Uranus et Neptune) et les étoiles les plus brillantes.
Ces différents objets possèdent un certain nombre d'attributs décrivant leur position dans le ciel et leur apparence, qui nous seront utiles pour les dessiner : leur position dans un système de coordonnées donné, leur taille angulaire, leur magnitude, etc. Les plus importants de ces attributs sont décrits ci-après.
2.2.1 Position
Comme nous l'avons vu à la §2.5 de l'étape 2, les étoiles ont la caractéristique d'avoir une position fixe dans le système équatorial, tout du moins à échelle humaine et à la précision qui nous intéresse ici. Tel n'est toutefois pas le cas des autres objets célestes gérés dans ce projet, comme les planètes, la Lune ou le Soleil, dont la position dans ce système change avec le temps.
Le système équatorial sera néanmoins le système principal dans lequel nous exprimerons la position des objets célestes, car le plus grand nombre d'entre eux — les étoiles — y ont une position fixe.
2.2.2 Taille angulaire
La taille angulaire (angular size) d'une sphère observée depuis un point donné est l'angle entre deux points opposés de la périphérie du disque vu par l'observateur. L'image de la figure 3 ci-dessous montre une sphère dont la taille angulaire est d'un demi degré pour l'observateur.
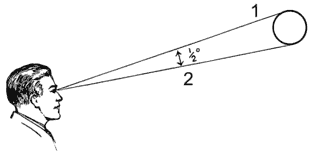
La Lune et le Soleil sont les deux seuls objets célestes dont la taille angulaire soit assez importante pour que, observés à l'œil nu, ils apparaissent comme des disques. Il se trouve d'ailleurs que leur taille angulaire est quasiment identique, ce qui permet au disque lunaire de recouvrir parfaitement le disque solaire lors d'éclipses totales.
Les étoiles et les planètes du système solaire ont quant à elles une taille angulaire tellement faible qu'elle n'est pas perceptible à l'œil nu, ni même avec des jumelles. Ces objets apparaissent donc dans le ciel comme de simples points, plus ou moins lumineux.
2.2.3 Magnitude
En astronomie, la luminosité des objets célestes telle qu'elle est perçue depuis la Terre est nommée leur magnitude apparente. La notion de magnitude absolue existe également, mais ne nous intéresse pas pour ce projet, et nous utiliserons donc dès maintenant le terme de magnitude pour désigner la magnitude apparente.
La magnitude d'un objet est mesurée sur une échelle quelque peu contre-intuitive, dans la mesure où plus un objet est brillant, et plus sa magnitude est petite, voir même négative ! La table ci-dessous donne quelques exemples de magnitude d'objets célestes importants.
| Objet | Magnitude | Note |
|---|---|---|
| Soleil | -26.7 | Objet le plus brillant du ciel |
| Lune | -12.9 | Au moment de la pleine Lune |
| Vénus | -4.9 | Planète la plus brillante du ciel |
| Sirius | -1.4 | Étoile la plus brillante du ciel |
| Rigel | 0.2 | Parmi les 10 étoiles les plus brillantes du ciel |
Il faut noter que les valeurs sont approximatives et dépendent de nombreux facteurs. Il n'est donc pas rare que différentes sources donnent des magnitudes différentes pour les mêmes objets.
A l'œil nu et dans les meilleures conditions d'observation qui soient, il peut être possible de discerner des objets de magnitude 6, mais généralement pas au-delà.
2.2.4 Phase
Certains objets célestes, p.ex. la Lune ou les planètes du système solaire, ont toujours un hémisphère qui fait face au Soleil et est donc illuminée par lui, tandis que l'autre hémisphère est dans l'ombre. Depuis la Terre, un tel objet apparaît donc comme un disque partiellement illuminé, le cas le plus connu étant bien entendu celui de la Lune.
Le pourcentage du disque visible depuis la Terre qui est illuminé par le Soleil s'appelle la phase, et est un nombre compris entre 0 et 1. Ainsi, la phase de la Lune vaut 1 au moment de la pleine Lune, et 0 au moment de la nouvelle Lune.
La magnitude d'un objet céleste ayant une phase dépend bien entendu de celle-ci.
3 Mise en œuvre Java
3.1 Classe CartesianCoordinates
La classe CartesianCoordinates du paquetage ….coordinates, publique, finale et immuable, représente des coordonnées cartésiennes.
Le constructeur de cette classe est privé, mais elle offre une méthode de construction, publique et bien entendu statique :
of(double x, double y), qui retourne les coordonnées cartésiennes d'abscissexet d'ordonnéey.
En plus de cette méthode de construction, la classe CartesianCoordinates offre deux méthodes d'accès :
double x(), qui retourne l'abscisse,double y(), qui retourne l'ordonnée.
Finalement, la classe CartesianCoordinates redéfinit les méthodes hashCode et equals pour qu'elles lèvent UnsupportedOperationException, et la méthode toString pour qu'elle retourne une représentation textuelle des coordonnées. Le format exact de cette représentation est libre, mais il doit au moins contenir la représentation textuelle de l'abscisse et de l'ordonnée.
3.2 Classe StereographicProjection
La classe StereographicProjection du paquetage ….coordinates, publique, finale et immuable, représente une projection stéréographique de coordonnées horizontales. Tout comme les classes représentant les changements de coordonnées sphériques décrites à l'étape précédente, elle implémente l'interface suivante :
Function<HorizontalCoordinates, CartesianCoordinates>
La classe StereographicProjection offre un unique constructeur public :
StereographicProjection(HorizontalCoordinates center), qui retourne la projection stéréographique centrée encenter.
Elle offre de plus les méthodes publiques suivantes, la méthode apply étant bien entendu celle définie (de manière abstraite) dans l'interface Function :
CartesianCoordinates circleCenterForParallel(HorizontalCoordinates hor), qui retourne les coordonnées du centre du cercle correspondant à la projection du parallèle passant par le pointhor; comme expliqué à la §2.1.3, l'ordonnée de ce centre peut être infinie,double circleRadiusForParallel(HorizontalCoordinates parallel), qui retourne le rayon du cercle correspondant à la projection du parallèle passant par le point de coordonnéeshor; comme expliqué à la §2.1.3, ce rayon peut être infini,double applyToAngle(double rad), qui retourne le diamètre projeté d'une sphère de taille angulaireradcentrée au centre de projection, en admettant que celui-ci soit sur l'horizon (voir §2.1.5),CartesianCoordinates apply(HorizontalCoordinates azAlt), qui retourne les coordonnées cartésiennes de la projection du point de coordonnées horizontalesazAlt,HorizontalCoordinates inverseApply(CartesianCoordinates xy), qui retourne les coordonnées horizontales du point dont la projection est le point de coordonnées cartésiennesxy.
Finalement, la classe StereographicProjection redéfinit les méthodes hashCode et equals pour qu'elles lèvent UnsupportedOperationException, et la méthode toString pour qu'elle retourne une chaîne dont le format est libre mais doit contenir au moins le texte StereographicProjection et les coordonnées du centre de la projection.
3.2.1 Conseils de programmation
- Performances
Tout comme les conversions de coordonnées représentées par les classes définies à l'étape précédente, la projection stéréographique se doit d'être rapide, car le nombre d'objets à projeter — en particulier les étoiles — est important.
Pour cette raison, et comme dans l'étape précédente, vous devez impérativement calculer dans le constructeur de la classe toutes les valeurs utilisées dans les formules de projection directe et inverse et qui ne dépendent que du centre de projection, et les stocker dans des attributs privés, ceci afin d'éviter leur calcul répété.
- Division par zéro
Les types
floatetdoublede Java possèdent chacun une valeur représentant l'infini positif et l'infini négatif. La division d'une valeur non nulle par zéro produit la valeur représentant l'infini, avec le bon signe. Par exemple, l'extrait de programme suivant :System.out.println(1.0 / 0.0)
affiche
Infinity.Dès lors, il n'est pas nécessaire de traiter de manière particulière le cas où les formules de la §2.1.3 font une telle division par zéro dans les méthodes retournant le centre et le rayon du cercle résultant de la projection d'un parallèle.
3.3 Classe CelestialObject
La classe CelestialObject du paquetage ….astronomy, publique, abstraite et immuable, sert de classe mère à toutes les classes représentant des objets célestes. Elle offre un unique constructeur, qui n'est visible que dans le paquetage contenant la classe (package private) :
CelestialObject(String name, EquatorialCoordinates equatorialPos, float angularSize, float magnitude), qui construit un objet céleste portant le nomname, situé aux coordonnées équatorialesequatorialPos, de taille angulaireangularSizeet de magnitudemagnitude, ou lèveIllegalArgumentExceptionsi la taille angulaire est négative, ouNullPointerExceptionsi le nom ou la position équatoriale sont nuls (c-à-d égaux ànull).
Attention : les deux derniers arguments de ce constructeur ont le type float et non pas double, et doivent être stockés dans des attributs de type float également, dans un souci d'économie de place. Pour mémoire, une valeur de type double occupe deux fois plus de place qu'une valeur de type float.
En plus de ce constructeur, la classe CelestialObject possède des méthodes d'accès publiques permettant d'obtenir les différentes valeurs données au constructeur. Ces méthodes, dont le comportement est évident et donc non décrit, sont :
String name(),double angularSize(),double magnitude(), etEquatorialCoordinates equatorialPos().
Notez toutefois que les deux méthodes du milieu retournent une valeur de type double malgré le fait que l'attribut qu'elles retournent ait le type float comme expliqué plus haut. Cela est volontaire.
Finalement, la classe CelestialObject offre la méthode publique suivante, qui par défaut retourne la même chose que la méthode name, mais qui pourra être redéfinie dans certaines sous-classes :
String info(), qui retourne un (court) texte informatif au sujet de l'objet, destiné à être montré à l'utilisateur.
De plus, CelestialObject redéfinit la méthode toString afin qu'elle retourne la même chose que la méthode info.
3.3.1 Conseils de programmation
Pour vérifier que les arguments du constructeur qui ne doivent pas être nuls ne le sont effectivement pas, utilisez la méthode requireNonNull de la classe Objects (avec un s à la fin !).
3.4 Classe Planet
La classe Planet du paquetage ….astronomy, publique, finale et immuable, est la sous-classe de CelestialObject représentant une planète. Elle n'offre rien d'autre qu'un constructeur public prenant exactement les mêmes arguments que celui de sa classe mère, dans le même ordre.
Notez bien que, étant donné que Planet est une classe immuable et que sa position équatoriale lui est passé à sa construction, une de ses instances ne peut représenter qu'une planète à un endroit donné ! Dès lors, pour produire p.ex. une animation du ciel, il sera nécessaire de recréer une nouvelle instance de Planet pour chaque image de l'animation.
3.5 Classe Moon
La classe Moon du paquetage ….astronomy, publique, finale et immuable, est la sous-classe de CelestialObject représentant la Lune à un instant donné. Elle possède un unique constructeur public :
Moon(EquatorialCoordinates equatorialPos, float angularSize, float magnitude, float phase), qui construit (un objet représentant) la Lune avec la position, la taille angulaire, la magnitude et la phase données, ou lèveIllegalArgumentExceptionsi la phase n'est pas comprise dans l'intervalle [0, 1].
Les arguments passés au constructeur de la classe mère doivent être tels que la méthode name retourne la chaîne Lune.
De plus, la classe Moon redéfinit la méthode info pour que la phase apparaisse après le nom, entre parenthèses et exprimé en pourcent, avec une décimale. Par exemple, si la phase est de 0.3752, la méthode info doit retourner la chaîne suivante :
Lune (37.5%)
3.6 Classe Sun
La classe Sun du paquetage ….astronomy, publique, finale et immuable, est la sous-classe de CelestialObject représentant le Soleil à un instant donné. Elle possède un unique constructeur public :
public Sun(EclipticCoordinates eclipticPos, EquatorialCoordinates equatorialPos, float angularSize, float meanAnomaly), qui construit (un objet représentant) le Soleil avec la position écliptique, la position équatoriale, la taille angulaire et l'anomalie moyenne données, ou lèveNullPointerExceptionsi la position écliptique est nulle. (La notion d'anomalie moyenne sera décrite dans une étape ultérieure.)
Les arguments passés au constructeur de la classe mère doivent être tels que la méthode name retourne la chaîne Soleil, et la méthode magnitude la valeur -26.7.
En plus de ce constructeur, la classe Sun offre les méthodes d'accès publiques suivantes, au comportement évident :
EclipticCoordinates eclipticPos(),double meanAnomaly().
3.7 Tests
Comme d'habitude, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.
4 Résumé
Pour cette étape, vous devez :
- écrire les classes
CartesianCoordinates,StereographicProjection,CelestialObject,Planet,MoonetSunselon les instructions données plus haut, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 20 mars 2020 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !