Coordonnées sphériques

Un système de coordonnées sphérique est un système de coordonnées tridimensionnel qui peut être vu comme une extension à trois dimensions d'un système polaire et dans lequel la position d'un point est donnée par :

• le rayon ρ qui est la distance entre le point et l'origine du repère utilisé,
• la longitude λ et la latitude ϕ, deux angles dont la définition exacte est donnée plus bas.

Au même titre que des coordonnées polaires permettent de représenter la position de n'importe quel point dans le plan, les coordonnées sphériques permettent de représenter la position de n'importe quel point dans l'espace. Cela dit, elles sont plus simples à comprendre si on admet que tous les points dont on désire représenter la position se trouvent à la surface d'une sphère dont le centre est l'origine du repère utilisé. Dans ce cas, le rayon de chacun des points est identique, et les deux coordonnées restantes — la longitude et la latitude — suffisent donc à représenter leur position.

Dans la totalité des cas dans lesquels nous utiliserons des coordonnées sphériques dans ce projet, nous pourrons justement faire l'hypothèse que tous les points qui nous intéressent sont à la surface d'une sphère. Nous ignorerons donc dès maintenant le rayon et ferons l'hypothèse que la position d'un point est toujours totalement déterminée par sa longitude et sa latitude, qu'il est temps de décrire.

La figure 1 ci-dessous illustre une sphère, centrée en O, à la surface de laquelle se trouvent les points dont nous désirons décrire la position. L'un d'eux, P, est également représenté, de même que sa longitude λ et sa latitude ϕ.

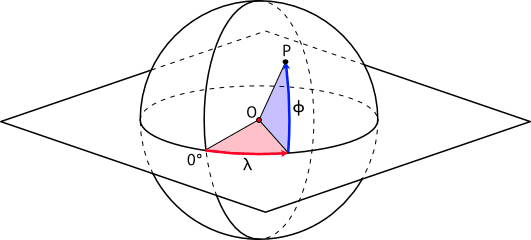
Cette figure montre aussi les deux entités qui doivent être choisies pour pouvoir déterminer les coordonnées de points et qui sont :

1. le plan de référence qui passe par le centre de la sphère et détermine tous les points de latitude 0, et
2. la direction de référence, notée 0°, qui détermine les points de longitude 0.

Une fois ces entités choisies, les coordonnées d'un point P sont déterminées ainsi :

• la longitude λ est l'angle entre la direction de référence et la projection de P sur le plan de référence,
• la latitude ϕ est l'angle entre P et le plan de référence.

La longitude couvre une plage de 360°, qui varie en fonction des systèmes de coordonnées mais qui est soit l'intervalle [0°, 360°[, soit l'intervalle [–180°, +180°[. Un demi-cercle de longitude constante se nomme un méridien, et celui de longitude 0 est visible sur la figure ci-dessus.

La latitude est quant à elle toujours comprise dans l'intervalle [–90°, +90°]. Les points de latitude positive se trouvent sur l'une des deux hémisphères déterminées par le plan de référence, les points de latitude négative dans l'autre. Un cercle de latitude constante se nomme un parallèle, et le cercle résultant de l'intersection du plan de référence et de la sphère est le parallèle de latitude 0.

Le système de coordonnées sphérique le plus connu est certainement le système géographique, utilisé pour représenter la position des points à la surface de la Terre, illustré ci-dessous.

Dans ce système, on suppose que la Terre est une sphère de 6371 km de rayon, et le plan de référence est celui de l'équateur. La direction de référence place la longitude 0° sur le méridien passant par l'observatoire royal de Greenwich, dans la banlieue de Londres, communément appelé le méridien de Greenwich.¹

La longitude est comprise dans l'intervalle [–180°, +180°[², les valeurs positives étant à l'est du méridien de référence, les valeurs négatives à l'ouest.

Le système de coordonnées géographique sera utile dans ce projet pour représenter la position de l'observateur, que l'on supposera situé à la surface de la Terre.

Si l'utilisation d'un système de coordonnées sphérique pour représenter la position de points situés à la surface de la Terre paraît naturelle, il n'en va pas forcément de même lorsqu'il s'agit de décrire la position d'objets astronomiques comme les étoiles ou les planètes. En effet, ces objets ne sont pas tous situés à la surface d'une sphère quelconque, mais bien répartis dans l'espace.

Néanmoins, du point de vue d'un observateur qui regarde le ciel, le fait que les différents objets visibles soient situés à des distances très différentes de lui n'a pas vraiment d'importance, et n'est d'ailleurs même pas observable à l'œil nu. Il est donc tout à fait possible de considérer que ces différents objets sont tous situés à la même distance (inconnue) de l'observateur, un peu comme s'ils étaient projetés sur un écran sphérique au centre duquel l'observateur se trouverait.

Cette idée, qui consiste à supposer que les objets astronomiques sont tous situés à la surface d'une sphère de rayon inconnu (et sans importance), est à la base de ce que l'on nomme les systèmes de coordonnées célestes. Les trois autres systèmes de coordonnées sphériques utilisés dans ce projet, décrits plus bas, sont de ce type.

La sphère imaginaire utilisée par les différents systèmes célestes s'appelle la sphère céleste. Notez que même si on a tendance à parler de la sphère céleste, il en existe en réalité plusieurs. Chaque système de coordonnées utilise ainsi une sphère céleste qui lui est propre, et dont le centre est parfois l'observateur, parfois le centre de la Terre, ou un autre point en fonction des besoins.

Le système de coordonnées horizontales est un système céleste dont la sphère céleste est centrée sur l'observateur, qui se trouve sur la surface de la Terre.

Le plan de référence du système horizontal est le plan de l'horizon, et la direction de référence est le nord (le sud est parfois aussi utilisé en astronomie, mais nous ne suivrons pas cette convention dans ce projet). La position d'un objet est donc déterminée par deux coordonnées qui correspondent à la longitude et à la latitude, mais qui portent un nom différent pour éviter les confusions. Il s'agit de :

• l'azimut (azimuth en anglais, souvent abrégé az), qui est l'angle entre la direction de référence (le nord) et le plan vertical contenant l'objet,
• la hauteur (altitude en anglais, souvent abrégé alt), aussi appelée l'élévation, qui est l'angle vertical entre le plan horizontal et l'objet.

L'azimut est compris dans l'intervalle [0°, 360°[ et correspond à la longitude, tandis que la hauteur est comprise dans l'intervalle [–90°, +90°] correspond à la latitude. Le point dont la hauteur vaut +90°, et qui est donc situé à la verticale de l'observateur, est appelé le zénith.

La figure ci-dessous illustre le système horizontal. L'observateur se trouve au centre de l'hémisphère, indiqué par O, et le plan de l'horizon est grisé. La position du point observé (en rouge) est décrite par son azimut a et son élévation h. Seule l'hémisphère visible par l'observateur (c-à-d située au-dessus de l'horizon) est représentée ici.

Le système horizontal est idéal pour l'observation, car un observateur connaissant les coordonnées d'un objet sait immédiatement où regarder dans le ciel pour le trouver. L'azimut lui dit dans quelle direction regarder, tandis que la hauteur lui dit à quelle hauteur au-dessus de l'horizon regarder. De plus, le signe de la hauteur permet de savoir si un objet est visible ou non, puisque seuls les objets dont la hauteur est positive sont visibles (en première approximation).

La figure ci-dessous montre les azimuts correspondants aux quatre points cardinaux (nord, sud, est et ouest) ainsi qu'aux quatre points intercardinaux principaux (nord-est, nord-ouest, sud-est et sud-ouest). La zone blanche est l'octant entourant le nord et tout azimut correspondant à cette zone sera, dans certaines situations, considéré comme équivalent au nord. Des zones de même tailles, non dessinées, entourent chacun des points cardinaux et intercardinaux.

Référence : Practical Astronomy with your Calculator or Spreadsheet, §17

Le système de coordonnées équatoriales est un système céleste dont la sphère céleste est généralement concentrique à la Terre, c-à-d que son centre est celui de la Terre.

Le plan de référence est le plan de l'équateur terrestre, et la direction de référence est un point nommé le point vernal, situé à l'intersection du plan de l'équateur et de celui de l'écliptique. Pour mémoire, l'écliptique est le plan dans lequel la Terre orbite autour du soleil.

Dans le système équatorial, la position d'un objet est donnée par deux coordonnées qui, comme toujours, correspondent à la longitude et à la latitude mais portent un nom différent. Il s'agit de :

• l'ascension droite (right ascension en anglais, souvent abrégé ra), qui correspond à la longitude,
• la déclinaison (declination en anglais, souvent abrégé dec), qui correspond à la latitude.

L'ascension droite est comprise dans l'intervalle [0°, 360°[ mais elle est généralement exprimée en heures, comprises dans l'intervalle [0h, 24h[.

La déclinaison est comprise, comme tous les équivalents de la latitude, dans l'intervalle [–90°, +90°].

L'intérêt principal des coordonnées équatoriales en astronomie est que celles des étoiles sont fixes, en tout cas à échelle humaine et à la précision qui nous intéresse ici. Par exemple, l'étoile Rigel se trouve à la position équatoriale fixe (5.2423h, –8.2016°).

Référence : Practical Astronomy with your Calculator or Spreadsheet, §18

Le système de coordonnées écliptiques est très similaire au système de coordonnées équatoriales, la différence principale étant le plan de référence, qui est le plan de l'écliptique plutôt que l'équateur. La direction de référence est la même que celle du système équatorial, à savoir le point vernal. Le centre de la sphère céleste est parfois aussi le centre du Soleil plutôt que celui de la Terre.

Dans le système écliptique, la position d'un objet est donné par les deux coordonnées suivantes :

• la longitude écliptique (ecliptic longitude en anglais), généralement notée λ,
• la latitude écliptique (ecliptic latitude en anglais), généralement notée β (et pas ϕ comme l'est habituellement la latitude).

L'intérêt principal des coordonnées écliptiques en astronomie est que les planètes du système solaire orbitent toutes dans des plans qui sont proches de l'écliptique, et leur latitude écliptique est donc toujours proche de zéro.

Référence : Practical Astronomy with your Calculator or Spreadsheet, §19

Dans un système de coordonnées sphériques quelconque, l'angle séparant deux points de coordonnées \((\lambda_1,\phi_1)\) et \((\lambda_2,\phi_2)\) s'appelle la distance angulaire (angular distance en anglais). Elle peut se déterminer au moyen de la formule suivante :

\[ \Delta\sigma = \arccos\left[ \sin\phi_1\,\sin\phi_2 + \cos\phi_1\,\cos\phi_2\cos(\lambda_1 - \lambda_2) \right] \]

En astronomie, il est souvent utile de calculer la distance angulaire entre deux objets visibles, dans le système horizontal. Cela permet par exemple à un observateur de trouver facilement le second d'entre eux si le premier a déjà été trouvé. Il peut s'aider pour cela du fait que la distance angulaire couverte par un doigt de la main au bout d'un bras tendu est d'environ 2°, et celle du poing fermé d'environ 10°.

La distance angulaire peut néanmoins se calculer dans n'importe quel système sphérique, et permet par exemple de déterminer la distance séparant deux points à la surface de la Terre. Ainsi, le Learning Center de l'EPFL se trouve aux coordonnées géographiques suivantes :

\[ (\lambda_1 = 6.5682°, \phi_1 = 46.5183°) \]

tandis que le bâtiment principal de l'EPFZ à Zürich se trouve aux coordonnées suivantes :

\[(\lambda_2 = 8.5476°, \phi_2 = 47.3763°)\]

En substituant ces valeurs dans l'équation ci-dessus, on obtient une distance angulaire d'environ 0.0279 radians. Sachant que la Terre a un rayon moyen de 6371 km, une simple multiplication nous permet de conclure que la distance séparant ces deux bâtiments est d'environ 178 km.

La classe SphericalCoordinates du paquetage ….coordinates, package private et abstraite, sert de classe mère à toutes les classes représentant des coordonnées sphériques.

Son constructeur est lui aussi package private, et il prend en argument la longitude et la latitude, qu'il stocke dans des attributs privés.

Les quatre méthodes qu'offre la classe SphericalCoordinates sont toutes package private et ont pour seul but de faciliter la mise en œuvre des méthodes similaires dans les sous-classes. Elles permettent d'obtenir chacune des deux coordonnées, soit en radians, soit en degrés. Il s'agit de :

• double lon(), qui retourne la longitude,
• double lonDeg(), qui retourne la longitude en degrés,
• double lat(), qui retourne la latitude,
• double latDeg(), qui retourne la latitude en degrés.

Finalement, la classe SphericalCoordinates, exactement comme Interval, redéfinit les méthodes hashCode et equals de Object afin qu'elles lèvent l'exception UnsupportedOperationException. Pour garantir qu'aucune sous-classe ne puisse les redéfinir, ces méthodes sont déclarées finales.

La classe GeographicCoordinates du paquetage ….coordinates, publique, finale et immuable, hérite de SphericalCoordinates et représente des coordonnées géographiques.

Son constructeur est privé, mais elle offre une méthode de construction statique :

• GeographicCoordinates ofDeg(double lonDeg, double latDeg), qui retourne les coordonnées géographiques dont la longitude en degrés est égale à lonDeg et la latitude en degrés est égale à latDeg, ou lève IllegalArgumentException si l'une ou l'autre de ces composantes est invalide (voir §2.2).

De plus, GeographicCoordinates offre des méthodes publiques et statiques permettant de vérifier si un angle en degrés représente une longitude ou une latitude valide. Ces méthodes, qui seront utiles dans l'interface graphique pour valider les coordonnées géographiques entrées par l'utilisateur, sont :

• boolean isValidLonDeg(double lonDeg), qui retourne vrai ssi l'angle qui lui est passé représente une longitude valide en degrés,
• boolean isValidLatDeg(double latDeg), qui retourne vrai ssi l'angle qui lui est passé représente une latitude valide en degrés.

La classe GeographicCoordinates offre de plus les 4 méthodes d'accès publiques suivantes :

• double lon(), qui retourne la longitude,
• double lonDeg(), qui retourne la longitude en degrés,
• double lat(), qui retourne la latitude,
• double latDeg(), qui retourne la latitude en degrés.

Finalement, elle redéfinit la méthode toString de manière à ce que l'appel suivant :

System.out.println(GeographicCoordinates.ofDeg(6.57, 46.52));

affiche :

(lon=6.5700°, lat=46.5200°)

Notez que les quatre décimales données suffisent largement, sachant que 0.0001° représente dans le pire cas une distance d'à peine plus de 10 m à la surface de la Terre.

La classe HorizontalCoordinates du paquetage ….coordinates, publique, finale et immuable, hérite de SphericalCoordinates et représente des coordonnées horizontales.

Son constructeur est privé, mais elle offre deux méthodes de construction (publiques et statiques) permettant de créer des coordonnées horizontales à partir d'angles en radians ou en degrés :

• HorizontalCoordinates of(double az, double alt), qui retourne les coordonnées horizontales dont l'azimut vaut az et la hauteur alt, ou lève IllegalArgumentException si l'une ou l'autre de ces composantes est invalide (voir §2.4),
• HorizontalCoordinates ofDeg(double azDeg, double altDeg), qui retourne les coordonnées horizontales dont l'azimut vaut azDeg en degrés et la hauteur vaut altDeg en degrés, ou lève IllegalArgumentException si l'une ou l'autre de ces composantes est invalide.

De plus, la classe HorizontalCoordinates offre les méthodes publiques suivantes :

• double az(), qui retourne l'azimut,
• double azDeg(), qui retourne l'azimut en degrés,
• String azOctantName(String n, String e, String s, String w), qui retourne une chaîne correspondant à l'octant dans lequel se trouve l'azimut du récepteur, chaîne formée en combinant les chaînes n, e, s et w correspondant aux quatre points cardinaux (resp. nord, est, sud et ouest), comme décrit ci-dessous,
• double alt(), qui retourne la hauteur,
• double altDeg(), qui retourne la hauteur en degrés,
• double angularDistanceTo(HorizontalCoordinates that), qui retourne la distance angulaire entre le récepteur (this) et le point donné en argument (that).

De plus, la classe HorizontalCoordinates redéfinit la méthode toString afin que l'appel suivant :

System.out.println(HorizontalCoordinates.ofDeg(350, 7.2));

provoque l'affichage suivant :

(az=350.0000°, alt=7.2000°)

La méthode azOctantName a pour but de retourner la chaîne représentant l'octant auquel correspond l'azimut des coordonnées. Chaque octant couvre une zone de 45° centrée sur chaque point cardinal ou intercardinal, comme illustré à la figure 4.

Ainsi, l'appel suivant :

System.out.println(HorizontalCoordinates.ofDeg(335, 0)
		   .azOctantName("N", "E", "S", "O"));

doit afficher NO, pour nord-ouest.

La classe EquatorialCoordinates du paquetage ….coordinates, publique, finale et immuable, hérite de SphericalCoordinates et représente des coordonnées équatoriales.

Cette classe est extrêmement similaire aux autres classes ci-dessus, et elle ne sera donc pas décrite en détail, seule une liste de méthodes à (re)définir est donnée ci-dessous, leur comportement devrait être évident.

Notez que cette similarité implique que pour gagner du temps, vous pouvez utiliser la commande Copy Class… du menu Refactor d'IntelliJ pour copier une des classes ci-dessous avant d'effectuer les renommages nécessaires au moyen de la commande Rename… du même menu.

La classe EquatorialCoordinates offre la méthode de construction suivante :

• EquatorialCoordinates of(double ra, double dec)

et les méthodes d'accès suivantes :

• double ra(),
• double raDeg(),
• double raHr(),
• double dec(),
• double decDeg().

Finalement, elle redéfinit la méthode toString, qui produit un résultat similaire à ceci :

(ra=1.5000h, dec=45.0000°)

Notez bien que l'ascension droite est exprimée en heures !

La classe EclipticCoordinates du paquetage ….coordinates, publique, finale et immuable, hérite de SphericalCoordinates et représente des coordonnées écliptiques.

Toute comme la classe précédente, celle-ci ne sera pas décrite en détail, pour les mêmes raisons. Elle offre la méthode de construction suivante :

• EclipticCoordinates of(double lon, double lat)

et les méthodes d'accès suivantes :

• double lon(),
• double lonDeg(),
• double lat(),
• double latDeg().

Finalement, elle redéfinit la méthode toString, qui produit un résultat similaire à ceci :

(λ=22.5000°, β=18.0000°)

À partir de cette étape, nous ne vous fournissons plus de tests unitaires, et il vous faut donc les écrire vous-même.

Pour vous laisser le temps de le faire, cette étape a volontairement été gardée aussi simple que possible. Profitez donc de cette occasion pour vous familiariser avec le processus d'écriture de tests.

Notez que si nous ne vous fournissons pas de tests JUnit, nous vous fournissons néanmoins une archive Zip à importer dans votre projet et contenant un fichier nommé SignatureChecks_2.java. La classe qu'il contient fait référence à la totalité des classes et méthodes de cette étape, ce qui vous permet de vérifier que leurs noms et types sont corrects. Cela est capital, car la moindre faute à ce niveau empêcherait l'exécution de nos tests unitaires.

Nous vous fournirons de tels fichiers pour toutes les étapes jusqu'à la mi-semestre, et il vous faudra penser à vérifier systématiquement qu'aucune erreur n'est signalée à leur sujet. Faute de cela, votre rendu pourrait se voir refusé par notre système.