Calcul de panorama
Etape 6

1 Introduction

Le but de cette étape, la dernière avant le rendu intermédiaire, est d'écrire les classes permettant de calculer un panorama et de stocker le résultat de ce calcul.

Cette étape devra être rendue deux fois :

pour le rendu testé habituel (délai : 31 mars, 16h30),
pour le rendu intermédiaire (délai : 7 avril, 16h30).

Le deuxième de ces rendus sera corrigé par lecture de votre code pour les étapes 1 à 6, et il vous faudra donc soigner sa qualité et sa documentation.

1.1 Calcul de panorama

Le dessin d'un panorama se fait au moyen d'une technique relativement simple basée sur le lancer de rayons. Pour faciliter sa compréhension, un panorama concret est utilisé, dont les paramètres sont :

position de l'observateur : non spécifiée,
altitude de l'observateur : 2000 m,
azimut du centre du panorama : 180°,
angle de vue horizontal : 80°,
distance maximale : 100 km,
largeur : 9 pixels,
hauteur : 5 pixels.

La petite taille (largeur et hauteur) de ce panorama le rend peu intéressant en pratique, mais facilite les explications qui suivent.

Etant donnés ces paramètres, il devrait être clair que le dessin de ce panorama produit une image de 9×5 pixels (45 au total), et que la correspondance entre les colonnes (resp. les lignes) de pixels et les azimuts (resp. les élévations) est celle donnée par la figure ci-dessous, similaire à la figure 5 de l'étape 5.

Figure 1 : Panorama de 9×5 pixels

Sur cette figure, les azimuts correspondants aux 9 colonnes de pixels apparaissent au-dessus de chacune d'entre elles, tandis que les élévations correspondant aux 5 lignes apparaissent à leur droite. Finalement, les index des quatre pixels situés dans les coins sont donnés.

Sachant qu'à chaque colonne de pixels correspond un azimut, on peut leur associer à chacune un profil altimétrique dont l'origine est la position de l'observateur, l'azimut est celui de la colonne et la longueur est la distance maximale. Vus du dessus, ces profils altimétriques sont donc répartis uniformément sur la zone visible du panorama, comme illustré par la figure ci-dessous.

Figure 2 : Les 9 profils du panorama d'exemple, vus du dessus

Une fois ce découpage effectué, chacun des profils altimétrique peut être dessiné de manière indépendante, pour obtenir la colonne de pixels lui correspondant.

1.1.1 Lancer de rayons

Le dessin de la colonne correspondant à un profil altimétrique se fait au moyen d'une technique nommée lancer de rayon (ray tracing en anglais). Le lancer de rayon consiste à simuler la trajectoire de rayons lumineux partant de l'observateur à différents angles, à déterminer à quelle distance ils atteignent le sol — à supposer qu'ils l'atteignent — puis à colorier le pixel correspondant en fonction du résultat.

La figure ci-dessous illustre ce principe en montrant cinq rayons partant de l'observateur, situé à l'extrémité gauche du profil altimétrique. Chacun de ces rayons correspond à une élévation différente : le plus bas à -20°, le suivant à -10°, etc. Dans cet exemple, les trois rayons du bas atteignent le sol, tandis que les deux du haut ne l'atteignent jamais, ou en tout cas pas dans les limites du profil.

Figure 3 : Lancer de 5 rayons sur un profil

Les rayons étant des droites, leur altitude en fonction de la position \(x\) le long du profil altimétrique s'exprime très facilement sous la forme d'une fonction :

\[ r(x) = r_0 + x\,\tan\alpha \]

où \(r_0\) est l'altitude de l'observateur, ici 2000 m, et \(\alpha\) l'angle d'élévation du rayon. Cette équation sera utile plus tard pour déterminer l'intersection d'un rayon avec le sol.

Il est possible de raccourcir nettement la longueur des rayons à simuler en choisissant judicieusement l'ordre de leur lancer. En effet, il est clair que tous les rayons situés au-dessus d'un rayon donné ne peuvent atteindre le sol que plus loin que lui — ou exactement à la même distance si le terrain est vertical.

Dès lors, en lançant les rayons de bas en haut, il est possible de déterminer leur intersection avec le sol de manière beaucoup plus efficace que ne le suggère la première figure ci-dessus. Cette idée est illustrée graphiquement dans la figure ci-dessous, les lignes pleines représentant des rayons comme précédemment, et les lignes traitillées représentant les parties des rayons originaux que cette optimisation permet de ne pas simuler.

Figure 4 : Lancer optimisé de 5 (morceaux de) rayons

1.1.2 Courbure terrestre

La technique de lancer de rayon décrite ci-dessus ne tient pas compte d'une caractéristique importante de la Terre : elle n'est pas plate.

Les profils altimétriques donnant (en gros) la distance entre la surface de la Terre et la sphère la modélisant, il n'est évidemment pas correct de supposer, par exemple, qu'un rayon horizontal a une altitude constante. Cela reviendrait à supposer qu'il suit la surface terrestre, impliquant entre autres qu'un observateur pourrait se voir de dos en utilisant un téléscope très puissant.

Ce problème peut être résolu de deux manières : en utilisant des rayons courbes plutôt que droits, ou en ajustant les altitudes des profils altimétriques en fonction de la distance à l'observateur. C'est cette seconde solution que nous utiliserons.

La figure ci-dessous montre la distance \(d\) entre un rayon rouge tangent à un grand cercle et le grand cercle lui-même, c-à-d la surface de la Terre. Cette distance est celle qui doit être soustraites des altitudes données par les profils altimétriques, et elle varie bien entendu en fonction de la distance à l'observateur, notée \(x\) sur cette figure.

Figure 5 : Distance entre un rayon horizontal et la surface de la Terre

La formule suivante donne cette distance \(d\) en fonction de la distance \(x\) à l'observateur, \(R\) étant le rayon de la Terre :

\[ d(x) = R - \sqrt{R^2 - x^2} \]

1.1.3 Courbure terrestre approximée

Pour éviter le calcul (coûteux) de la racine carrée, il peut être intéressant d'approximer la formule précédente par une autre, plus simple. Sachant que la distance \(x\) sera toujours très petite par rapport au rayon de la Terre, l'utilisation d'une série de Taylor tronquée peut convenir.

En déterminant la série de Taylor de la formule ci-dessus et en ne gardant que son premier terme, on obtient la formule approximative suivante :

\[ d^\dagger(x) = \frac{x^2}{2 R} \]

Pour déterminer sa validité, il est important de comparer les valeurs qu'elle produit avec celles produites par la formule exacte. La table ci-dessous donne la valeur de ces deux formules pour des distances allant de 0 à 500 km, ainsi que la différence entre elles, \(\Delta_d(x) = d(x) - d^\dagger(x)\). Notez que la distance \(x\) est donnée en kilomètres alors que les autres valeurs sont en mètres.

\(x\)	\(d(x)\)	\(d^\dagger(x)\)	\(\Delta_d(x)\)
0	0	0	0
100	785	785	0
200	3140	3139	1
300	7067	7063	4
400	12569	12557	12
500	19650	19620	30

On constate que la différence entre ces deux formules est négligeable, valant au plus 30 m pour une distance de 500 km. Sachant que le record actuel de visibilité semble être d'environ 450 km¹, cette précision est largement suffisante.

1.1.4 Réfraction atmosphérique

Tenir compte de la courbure de la Terre ne suffit pas pour calculer des panoramas conformes à la réalité. En effet, la lumière ne se déplace pas en ligne droite dans l'atmosphère, mais de manière courbe, en raison de la densité variable des couches d'air qu'elle traverse.

Ce phénomène, nommé réfraction atmosphérique, est malheureusement presque impossible à modéliser correctement, car la densité de l'air varie en fonction de nombreux facteurs comme l'altitude, le gradient de température, l'humidité, etc.

Néanmoins, la réfraction a pour effet général de courber les rayons lumineux dans la même direction que la surface terrestre, rendant visibles des objets qui ne le seraient normalement pas. Dès lors, une manière simple de tenir compte de la réfraction consiste à supposer que la Terre est plus plate qu'elle ne l'est réellement, donc que son rayon est plus grand.

Pour ce faire, on définit le rayon effectif de la Terre, \(R_e\), en fonction de son rayon réel \(R\) et d'une constante \(k\) nommée coefficient de réfraction :

\[ R_e = \frac{R}{1 - k} \]

La valeur généralement utilisée pour \(k\) est 0.13. On la doit à Gauss, qui l'a déterminée au moyen de mesures effectuées dans les environs de Göttingen, où il travaillait.

En substituant le rayon effectif \(R_e\) au rayon réel \(R\) dans l'équation de la section précédente, on obtient la formule finale pour l'ajustement à apporter aux altitudes des profils altimétriques en fonction de la distance à l'utilisateur :

\[ d^*(x) = \frac{x^2}{2 R_e} = \frac{1 - k}{2R}\,x^2 \]

1.1.5 Distance rayon-sol

En combinant les différentes formules ci-dessus, on peut déterminer celle donnant la distance séparant un rayon du sol en fonction de la distance (horizontale) à l'observateur. Elle s'obtient simplement en soustrayant de l'altitude du rayon celle du profil, représentée par la fonction \(p\) ci-dessous, en prenant soin d'ajuster cette dernière pour tenir compte de la courbure de la Terre et de la réfraction :

\[ \delta(x) = r(x) - \left[p(x) - d^*(x)\right] \]

En substituant dans cette formule les définitions de \(r\) et \(d^*\), on obtient :

\begin{align*} \delta(x) &= r(x) - \left[p(x) - d^*(x)\right]\\ &= r_0 + x\,\tan\alpha - \left[p(x) - \frac{1-k}{2R}x^2\right]\\ &= r_0 + x\,\tan\alpha - p(x) + \frac{1 - k}{2R} x^2 \end{align*}

La fonction \(\delta\) est fondamentale au calcul des panoramas, puisque ses zéros correspondent aux positions auxquelles le rayon intersecte le sol. En pratique, seul le premier de ces zéros — celui qui est le plus proche de l'origine, donc de l'observateur — nous intéresse.

1.2 Panorama

Dans la description du calcul du panorama ci-dessus, on a supposé que le résultat de ce calcul était une image. Il s'agit en fait d'une simplification, faite pour faciliter la compréhension.

La réalité est légèrement plus complexe : le processus de calcul du panorama ne produit pas directement une image, mais un certain nombre d'informations concernant les points atteints par chacun des rayons lancés au cours du calcul.

La principale information stockée pour chaque rayon est la distance parcourue par celui-ci avant d'atteindre le sol. Cette distance est infinie si le rayon n'atteint jamais le sol dans les limites du profil. Si elle ne l'est pas, les informations suivantes concernant le point de contact entre le rayon et le sol sont également stockées :

sa position (longitude et latitude),
l'altitude du terrain à cet endroit,
la pente du terrain à cet endroit.

Ces informations sont nommées échantillons (samples en anglais), car ils représentent effectivement des échantillons de différentes fonctions continues.

Une fois collectés, ces échantillons sont combinées d'une manière ou d'une autre pour obtenir une image du panorama, comme nous le verrons lors d'une étape ultérieure. Par exemple, pour le panorama présenté dans l'introduction au projet, la couleur de chaque pixel de l'image finale est déterminée en utilisant :

la distance parcourue par le rayon, qui donne la teinte du pixel,
la pente du terrain au point de contact, qui donne la luminosité du pixel : plus la pente est grande, plus le pixel est foncé.

Cette technique permet de bien distinguer les différentes chaînes de montagnes, puisqu'elles ont une teinte différente, et donne de plus une bonne impression de relief en assombrissant les pentes raides. Ainsi, sur l'extrait de ce panorama présenté à la figure 6 ci-dessous, on distingue bien trois chaînes successives de montagnes, de teinte différente car situées à différentes distances de l'observateur :

à l'avant-plan, une première chaîne turquoise — le Moléson et Teysachaux, dans les Préalpes fribourgeoises,
au milieu, une seconde chaîne rose — le Grand et le Petit Muveran, entre autres, dans les Alpes vaudoises,
à l'arrière-plan, une troisième chaîne verdâtre — le Grand Combin, dans les Alpes valaisannes.

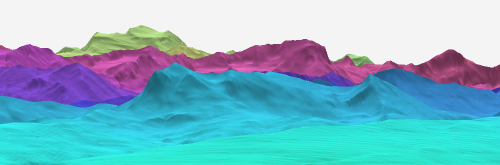
Figure 6 : Le Moléson, le Grand Muveran et le Grand Combin

2 Mise en œuvre Java

La classe représentant les panoramas étant immuable, elle est accompagnée d'un bâtisseur permettant au calculateur de panorama de construire progressivement son résultat. Les classes à réaliser pour cette étape sont donc au nombre de trois : celle représentant un panorama et stockant ses échantillons, son bâtisseur, et enfin le calculateur de panorama.

2.1 Classe `Panorama`

La classe Panorama du paquetage ch.epfl.alpano, publique et immuable (donc finale), représente un panorama.

Cette classe ne possède qu'un seul constructeur, et il est privé, pour la raison décrite plus bas. Il prend en arguments les paramètres du panorama — de type PanoramaParameters — ainsi que cinq tableaux de type float[] contenant les valeurs des échantillons pour chaque point : distance, longitude, latitude, altitude et pente. Tous ces tableaux ont une taille égale au nombre de points du panorama — le produit de sa largeur et de sa hauteur — et les échantillons y sont stockés selon leur index linéaire défini par la méthode sampleIndex de la classe PanoramaParameters, décrite à l'étape 5.

La raison pour laquelle le constructeur est privé est qu'il ne copie pas les tableaux qu'il reçoit mais se contente de les stocker tels quels. Ce comportement est très dangereux si n'importe qui peut appeler le constructeur, car rien ne garantit que l'appelant ne modifiera pas ultérieurement le contenu des tableaux, violant ainsi l'immuabilité de la classe. En rendant le constructeur privé, on peut s'assurer que seul le bâtisseur peut l'appeler, et garantir que celui-ci ne modifie jamais les tableaux ultérieurement.

Cette stratégie permet d'éviter la copie, assez coûteuse, de tableaux dont la taille peut être importante. Par exemple, le panorama présenté dans l'introduction au projet a une taille de 2500 par 800 échantillons, soit 2 millions d'échantillon. Etant donné qu'il y a cinq tableaux de cette taille et qu'une valeur de type float occupe 4 octets, cela représente au total 40 Mo de données.

En dehors de ce constructeur privé, la classe PanoramaParameters ne possède que des accesseurs. Le premier permet d'obtenir les paramètres :

PanoramaParameters parameters(),

tandis que les autres permettent d'obtenir la valeur d'un échantillon d'index donné :

float distanceAt(int x, int y),
float longitudeAt(int x, int y),
float latitudeAt(int x, int y),
float elevationAt(int x, int y), et
float slopeAt(int x, int y).

Tous ces accesseurs lèvent IndexOutOfBoundsException si les coordonnées du point passées sont hors des bornes du panorama.

Dans certains cas, il peut être utile d'obtenir une valeur par défaut plutôt qu'une exception lorsque l'index est hors des bornes, et c'est le but de la méthode suivante :

float distanceAt(int x, int y, float d), qui retourne la distance pour le point de coordonnées données, ou la valeur par défaut d si les coordonnées sont hors des bornes du panorama.

Il n'existe pas d'équivalent à cette méthode pour les autres données (position, altitude, pente).

2.2 Classe `Panorama.Builder`

La classe Builder, publique, finale et imbriquée statiquement dans la classe Panorama, représente un bâtisseur de panorama. Elle est dotée d'un unique constructeur public :

Builder(PanoramaParameters parameters), qui construit un bâtisseur de panorama dont les paramètres sont ceux donnés, ou lève l'exception NullPointerException s'ils sont nuls.

Initialement, tous les échantillons du panorama en construction (longitude, latitude, etc.) valent 0 pour tous les points, sauf la distance à l'observateur qui est infinie (c-à-d égale à Float.POSITIVE_INFINITY) pour tous les points. La méthode fill de la classe Arrays peut être utilisée pour faire cette initialisation.

La classe Builder offre cinq méthodes permettant de définir la valeur d'un échantillon du panorama en cours de construction à un index donné. Ces méthodes ont toutes un comportement similaire, à savoir :

si les coordonnées du point passées (l'index x, y) sont invalides, elles lèvent l'exception IndexOutOfBoundsException,
si la méthode build a déjà été appelée une fois sur ce bâtisseur, elles lèvent l'exception IllegalStateException,
elles retournent le bâtisseur lui-même comme résultat, afin de permettre le chaînage d'appels.

Ces méthodes sont :

Builder setDistanceAt(int x, int y, float distance),
Builder setLongitudeAt(int x, int y, float longitude),
Builder setLatitudeAt(int x, int y, float latitude),
Builder setElevationAt(int x, int y, float elevation), et
Builder setSlopeAt(int x, int y, float slope).

Finalement, la classe Builder offre une méthode de construction :

Panorama build(), qui construit et retourne le panorama, ou lève l'exception IllegalStateException si elle a déjà été appelée une fois.

En résumé, un bâtisseur de panorama peut bâtir au plus un panorama, car il est inutilisable après le premier appel à la méthode build. Comme expliqué plus haut, c'est ce comportement qui permet à la classe Panorama de réutiliser les tableaux passés à son constructeur sans les copier, tout en restant immuable.

2.3 Classe `PanoramaComputer`

La classe PanoramaComputer, du paquetage ch.epfl.alpano, publique et immuable (donc finale), représente un calculateur de panorama. Elle est dotée d'un unique constructeur public :

PanoramaComputer(ContinuousElevationModel dem), qui construit un calculateur de panorama obtenant les données du MNT continu passé en argument, ou lève l'exception NullPointerException s'il est nul.

En plus de ce constructeur, la classe PanoramaComputer offre une méthode publique permettant de calculer un panorama :

Panorama computePanorama(PanoramaParameters parameters), qui calcule et retourne le panorama spécifié par les paramètres.

Finalement, elle offre la méthode publique et statique suivante :

DoubleUnaryOperator rayToGroundDistance(ElevationProfile profile, double ray0, double raySlope), qui retourne la fonction donnant la distance entre un rayon d'altitude initiale ray0 et de pente de raySlope, et le profil altimétrique profile.

La fonction retournée par rayToGroundDistance n'est rien d'autre que la fonction \(\delta\) de la section 1.1.5, la pente du rayon étant égale à la tangente de l'angle d'élévation. Notez que cette fonction se définit très facilement au moyen d'une lambda, car DoubleUnaryOperator est une interface fonctionnelle.

2.3.1 Intersection rayon-sol

Pour déterminer l'intersection d'un rayon avec le sol, la méthode computePanorama utilise les méthodes firstIntervalContainingRoot et improveRoot écrites à l'étape 1, appliquées bien entendu à la fonction retournée par rayToGroundDistance.

La taille de l'intervalle à utiliser pour la recherche est de 64 m tandis que la taille de celui à utiliser pour l'amélioration par dichotomie est de 4 m. Ces valeurs constituent un bon compromis entre qualité de l'image finale et temps de calcul.

2.4 Tests

Comme d'habitude, nous ne vous fournissons pas de tests unitaires mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.

Nous vous conseillons néanmoins fortement d'écrire des tests unitaires pour cette étape, ainsi que de générer une image de test au moyen du programme décrit ci-dessous.

2.4.1 Dessin de panorama

Une manière de vous assurer que votre programme calcule correctement un panorama consiste à dessiner une image à partir du résultat qu'il produit. C'est le but du programme ci-dessous, qui dessine une image d'un panorama du Niesen vu depuis le lac de Thoune.

La technique de dessin utilisée est très simple : tous les points du panorama pour lesquels la distance est infinie sont coloriés en bleu ciel, les autres en une teinte de gris allant du noir (distance inférieure ou égale à 2 km) au blanc (distance supérieure ou égale à 17 km).

Comme précédemment, les énoncés d'importation ont été omis, de même que la méthode gray, identique à celle utilisée à l'étape 3.

final class DrawPanorama {
  final static File HGT_FILE = new File("N46E007.hgt");

  final static int IMAGE_WIDTH = 500;
  final static int IMAGE_HEIGHT = 200;

  final static double ORIGIN_LON = toRadians(7.65);
  final static double ORIGIN_LAT = toRadians(46.73);
  final static int ELEVATION = 600;
  final static double CENTER_AZIMUTH = toRadians(180);
  final static double HORIZONTAL_FOV = toRadians(60);
  final static int MAX_DISTANCE = 100_000;

  final static PanoramaParameters PARAMS =
    new PanoramaParameters(new GeoPoint(ORIGIN_LON,
                                        ORIGIN_LAT),
                           ELEVATION,
                           CENTER_AZIMUTH,
                           HORIZONTAL_FOV,
                           MAX_DISTANCE,
                           IMAGE_WIDTH,
                           IMAGE_HEIGHT);

  public static void main(String[] as) throws Exception {
    try (DiscreteElevationModel dDEM =
         new HgtDiscreteElevationModel(HGT_FILE)) {
      ContinuousElevationModel cDEM =
        new ContinuousElevationModel(dDEM);
      Panorama p = new PanoramaComputer(cDEM)
        .computePanorama(PARAMS);

      BufferedImage i =
        new BufferedImage(IMAGE_WIDTH,
                          IMAGE_HEIGHT,
                          TYPE_INT_RGB);

      for (int x = 0; x < IMAGE_WIDTH; ++x) {
        for (int y = 0; y < IMAGE_HEIGHT; ++y) {
          float d = p.distanceAt(x, y);
          int c = (d == Float.POSITIVE_INFINITY)
            ? 0x87_CE_EB
            : gray((d - 2_000) / 15_000);
          i.setRGB(x, y, c);
        }
      }

      ImageIO.write(i, "png", new File("niesen.png"));
    }
  }
}

En exécutant ce programme, vous devriez obtenir l'image ci-dessous, qui a été redimensionnée pour des questions de présentation mais qui est également disponible en taille réelle.

Figure 7 : Le Niesen

Pour comparer, l'image ci-dessous a été obtenue au moyen de Google Earth depuis le même point de vue.

Figure 8 : Le Niesen (image Google Earth)

3 Résumé

Pour cette étape, vous devez :

écrire les classes Panorama, Panorama.Builder et PanoramaComputer en fonction des indications données plus haut,
tester votre code,
documenter la totalité des entités publiques que vous avez définies,
rendre votre code au plus tard le 31 mars à 16h30, via le système de rendu.

N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus et aucun retard, aussi insignifiant soit-il, ne sera toléré !

Notes de bas de page

Ce record semble être détenu par un groupe d'espagnols ayant réussi à photographier le massif des Ecrins depuis les Pyrénées, soit une distance d'à peu près 440 km. En consultant leur blog à ce sujet, vous constaterez que même en disposant d'un bon téléobjectif et de conditions de visibilité idéales, les montagnes se trouvant à plus de 400 km sont à peine visibles.

Calcul de panorama Etape 6