Sommets et paramétrage du panorama
Etape 5
1 Introduction
Le but de cette étape est d'écrire les classes permettant de :
- représenter les sommets alpins et en lire une liste depuis un fichier,
- paramétrer le calcul d'un panorama.
Une fois cette étape terminée, tout sera en place pour enfin calculer des panoramas, ce qui constituera le sujet de l'étape suivante.
1.1 Sommets alpin
Le but de ce projet est non seulement de dessiner des panoramas, mais également de les annoter avec les noms des principaux sommets visibles. Cela implique de connaître le nom, la position et l'altitude des sommets alpins importants.
Pour cela, nous mettons à votre disposition une archive Zip contenant un unique fichier textuel nommé alps.txt, qui liste 21 069 sommets alpins. Tout comme les fichiers HGT, il provient du site Viewfinder Panoramas de Jonathan de Ferranti.
Le fichier alps.txt contient une ligne par sommet répertorié. Chacune de ces lignes contient les champs suivants à propos du sommet qu'elle décrit, dans l'ordre : sa longitude, sa latitude, son altitude, trois champs que nous ignorerons, et enfin son nom. Par exemple, les trois lignes ci-dessous décrivent trois sommets des Alpes bernoises, le Lauberhorn, l'Eiger et le Rotstock :
7:56:53 46:35:33 2472 H1 C02 D0 LAUBERHORN
8:00:19 46:34:39 3970 H1 C02 E0 EIGER
7:59:01 46:34:38 2663 H1 C02 E0 ROTSTOCK
Le format de chaque ligne est documenté sur le site Viewfinder Panoramas, mais le court résumé qui suit devrait suffire à l'analyser correctement.
Chaque champ commence à une position fixe de la ligne. Par exemple, la longitude commence toujours à la colonne 0 (la première), la latitude à la colonne 10, etc. Les coordonnées sont données en degrés, minutes et secondes, séparées par deux-points (:) et l'altitude est donnée en mètres. Le fichier est encodé en ASCII, et ne contient donc malheureusement aucune lettre accentuée.
1.2 Paramétrage du panorama
Le dessin d'un panorama requiert la connaissance d'un certain nombre de paramètres à son sujet. Pour ce projet, un panorama sera paramétré par :
- la position de l'observateur \(O\),
- l'altitude de l'observateur \(e\),
- l'azimut du centre du panorama \(a\),
- l'angle de vue horizontal \(v_h\),
- la distance maximale de visibilité \(d\),
- la largeur du panorama \(w\),
- la hauteur du panorama \(h\).
En gros, les cinq premiers paramètres déterminent la partie de la Terre qui est représentée sur le panorama, tandis que les deux derniers déterminent la taille de l'image rectangulaire finale.
La figure ci-dessous présente la partie de la Terre représentée sur le panorama, que nous nommerons la zone visible, et la signification des différents paramètres. La zone visible est un volume tridimensionnel difficile à décrire mais qui est un secteur de disque vu de dessus, et un triangle vu de profil. La figure présente ces deux vues de la zone visible, en blanc : à gauche, elle est vue de dessus, à droite, elle est vue de profil.
Figure 1 : Zone visible sur un panorama, en fonction des paramètres
Notez que l'angle de vue vertical, noté \(v_v\), ne fait pas partie des paramètres puisqu'il peut être calculé en fonction d'autres paramètres, comme nous le verrons plus bas.
1.2.1 Exemple
Les différents paramètres peuvent être illustrés au moyen du panorama donné dans l'introduction au projet, rappelé dans la figure ci-dessous.
Les paramètres de ce panorama sont :
- position de l'observateur : (6.8087°, 47.0085°),
- altitude de l'observateur : 1380 m,
- azimut du centre du panorama : 162°,
- angle de vue horizontal : 27°,
- distance maximale : 300 km,
- largeur : 2500 pixels,
- hauteur : 800 pixels.
La carte ci-dessous montre, en bleu, la zone visible dans ce panorama, vue de dessus. Elle correspond donc à la partie gauche de la figure 1. Notez que la distance maximale est trop importante pour être visible sur cette carte, raison pour laquelle la zone visible est tronquée au sud.
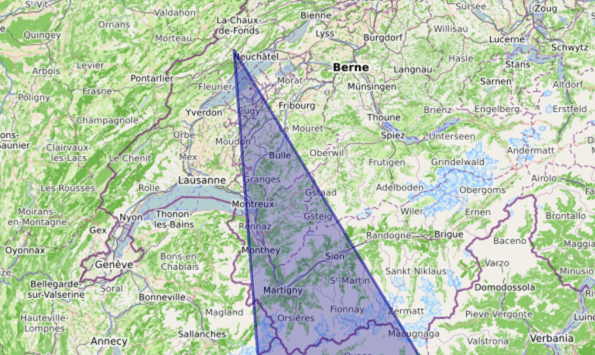
Figure 3 : Zone visible du panorama, du dessus (carte OpenStreetMap)
Cette zone visible peut également être visualisée de profil, ce qui est fait dans la figure ci-dessous. Pour faciliter sa compréhension, la zone visible y est présentée superposée à un profil altimétrique correspondant au centre du panorama, c-à-d à l'azimut 162°. Notez toutefois que cette représentation est quelque peu trompeuse, car le profil altimétrique ne prend pas en compte la courbure de la Terre.
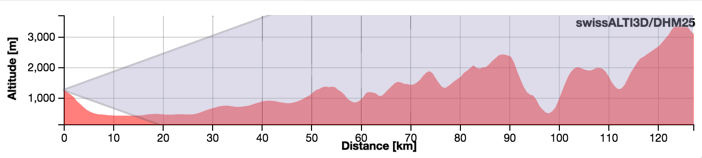
Figure 4 : Zone visible du panorama, de profil (données Swisstopo)
Les deux derniers paramètres, la largeur \(w\) et la hauteur \(h\), donnent les dimensions du panorama calculé. Dans un premier temps, nous pouvons considérer qu'il s'agit de la largeur et de la hauteur, en pixels, de l'image finale. Comme nous le verrons plus tard lorsque nous introduirons le suréchantillonnage, cela n'est pas strictement correct, mais nous pouvons l'ignorer pour l'instant.
La figure ci-dessous montre les pixels du panorama final, représentés par de petits cercles blancs régulièrement espacés. Ces pixels sont numérotés au moyen d'un index bidimensionnel, et celui du coin haut-gauche a l'index (0,0). Cette convention peut paraître surprenante mais est habituelle dans le monde du graphisme, raison pour laquelle nous l'adoptons ici.
Figure 5 : Image du panorama
Cette figure présente également la correspondance entre les paramètres déterminant la zone visible et les pixels. Ainsi, les \(w\) colonnes de pixels de l'image couvrent une zone qui correspond à l'angle de vue horizontal \(v_h\). De plus, l'azimut central correspond à la colonne de pixels centrale — ou se trouve entre deux colonnes si \(w\) est pair. Finalement, le centre vertical de l'image correspond à l'élevation de 0°, c-à-d à l'horizontale.
L'angle correspondant à l'espace entre deux pixels est identique horizontalement et verticalement, et est nommé \(\delta\) sur cette figure. Il se calcule aisément en fonction de l'angle de vue horizontal et de la largeur de l'image :
\[\delta = \frac{v_h}{w - 1} \]
Dès lors, l'angle de vue vertical peut également être calculé facilement :
\[ v_v = \delta(h - 1) = v_h\frac{h - 1}{w - 1} \]
2 Mise en œuvre Java
Les classes à écrire pour cette étape font partie de deux paquetages distincts : ch.epfl.alpano.summit, un nouveau paquetage contenant tout le code lié aux sommets, et ch.epfl.alpano, déjà existant.
2.1 Classe Summit
La classe Summit du paquetage ch.epfl.alpano.summit, publique et immuable (donc finale), représente un sommet. Elle possède un unique constructeur public :
Summit(String name, GeoPoint position, int elevation), qui construit un sommet dont le nom, la position et l'altitude sont ceux donnés, ou lève l'exceptionNullPointerExceptionsi le nom ou la position sont nuls.
En plus de ce constructeur, la classe Summit offre des accesseurs publics pour chacun de ses attributs (name, position et elevation), ainsi qu'une redéfinition de la méthode toString héritée de Object.
La méthode toString retourne une chaîne composée, dans l'ordre, du nom du sommet, de sa position et de son altitude. Par exemple, appliquée à l'objet représentant l'Eiger, elle retourne :
EIGER (8.0053,46.5775) 3970
2.2 Classe GazetteerParser
La classe GazetteerParser du paquetage ch.epfl.alpano.summit, publique et non instanciable (c-à-d dotée d'un constructeur privé et vide), représente un lecteur de fichier décrivant des sommets1. Elle possède une unique méthode publique (et statique), permettant de charger le contenu du fichier décrivant les sommets :
List<Summit> readSummitsFrom(File file), qui retourne un tableau dynamique non modifiable contenant les sommets lus depuis le fichierfile, ou lève l'exceptionIOExceptionen cas d'erreur d'entrée/sortie ou si une ligne du fichier n'obéit pas au format décrit plus haut.
Pour mémoire, un tableau dynamique non modifiable peut s'obtenir à partir d'un tableau dynamique (de type ArrayList) au moyen de la méthode unmodifiableList de la classe Collections (avec un s).
2.2.1 Lecture du fichier
La lecture du fichier décrivant les sommets peut se faire en combinant les trois types de flots suivants :
- un flot
FileInputStreampour lire les données du fichier sous forme d'octets, - un flot
InputStreamReaderpour transformer ce flot d'octets en un flot de caractères en utilisant l'encodage ASCII (représenté par l'attribut statiqueUS_ASCIIde la classeStandardCharsets), - un flot
BufferedReaderpour pouvoir facilement lire les caractères ligne par ligne au moyen de la méthodereadLine.
L'analyse des lignes individuelles peut quant à elle se faire au moyen des méthodes trim, substring et split de la classe String, et de la méthode parseInt de la classe Integer.
La méthode split permet de facilement découper une chaîne représentant un angle et dont les trois composantes (heures, minutes et secondes) sont séparées par deux-points (:), comme l'illustre l'exemple ci-dessous :
String angle = "12:34:56";
String[] hms = angle.split(":");
// hms[0] vaut "12", hms[1] vaut "34" et hms[2] vaut "56"
2.2.2 Méthodes privées
En plus de l'unique méthode publique et statique mentionnée ci-dessus, il est conseillé de définir une ou deux méthodes auxiliaires privées, par exemple :
- une méthode prenant une ligne en argument et retournant le sommet correspondant,
- une méthode prenant une chaîne contenant un angle exprimé en degrés, minutes et secondes et retournant l'angle correspondant, en radians.
2.3 Classe PanoramaParameters
La classe PanoramaParameters du paquetage ch.epfl.alpano, publique et immuable (donc finale), représente les paramètres nécessaires au dessin d'un panorama. Elle est dotée de l'unique constructeur public suivant :
PanoramaParameters(GeoPoint observerPosition, int observerElevation, double centerAzimuth, double horizontalFieldOfView, int maxDistance, int width, int height), qui construit un objet contenant les paramètres passés en argument et qui correspondent à ceux énumérés à la section 1.2 ; lève l'exceptionNullPointerExceptionsi la position de l'observateur est nulle, ou l'exceptionIllegalArgumentExceptionsi l'azimut central n'est pas canonique, si l'angle de vue horizontal n'est pas compris entre 0 (exclu) et \(2\pi\) (inclu) ou si la largeur, hauteur et distance maximales ne sont pas strictement positives.
Comme d'habitude dans ce projet, les angles sont spécifiés en radians, les distances et altitudes en mètres.
En dehors de ce constructeur, la classe PanoramaParameters contient un accesseur public pour chacun des argument passés au constructeur, de même type et de même nom (observerPosition, observerElevation, etc.). De plus, elle offre un accesseur pour l'angle de vue vertical, que l'on peut considérer comme un paramètre dérivé car il se calcule en fonction d'autres paramètres, comme expliqué plus haut :
double verticalFieldOfView(), qui retourne l'angle de vue vertical.
D'autre par, la classe PanoramaParameters offre des méthodes permettant de faire la correspondance entre les index des pixels et le système de coordonnées horizontales de l'observateur (azimut et élévation), correspondance illustrée à la figure 5 plus haut :
double azimuthForX(double x), qui retourne l'azimut canonique correspondant à l'index de pixel horizontalx, ou lève l'exceptionIllegalArgumentExceptionsi celui-ci est inférieur à zéro, ou supérieur à la largeur moins un,double xForAzimuth(double a), qui retourne l'index de pixel horizontal correspondant à l'azimut donné, ou lève l'exceptionIllegalArgumentExceptionsi cet azimut n'appartient pas à la zone visible,double altitudeForY(double y), qui retourne l'élévation (nommée, malheureusement, altitude en anglais) correspondant à l'index de pixel verticaly, ou lève l'exceptionIllegalArgumentExceptionsi celui-ci est inférieur à zéro, ou supérieur à la hauteur moins un,double yForAltitude(double a), qui retourne l'index de pixel vertical correspondant à l'élévation donnée, ou lève l'exceptionIllegalArgumentExceptionsi celle-ci n'appartient pas à la zone visible.
Les index de pixels utilisés par ces méthodes sont de type double, ce qui permet de désigner des positions situées entre les pixels et est parfois utile. Les qualifier d'index est dès lors un abus de langage, mais il ne devrait pas nuire à la compréhension.
Finalement, la classe PanoramaParameters offre des méthodes qui ne sont visibles que dans son paquetage :
boolean isValidSampleIndex(int x, int y), qui retourne vrai si et seulement si l'index passé est un index de pixel valide,int linearSampleIndex(int x, int y), qui retourne l'index linéaire du pixel d'index donné.
L'index linéaire est simplement un index à une dimension, qui vaut 0 pour le pixel d'index (0,0), 1 pour celui d'index (1,0), et ainsi de suite jusqu'au pixel en bas à droite de l'image, dont l'index est \((w-1, h-1)\) et l'index linéaire \(w\cdot h - 1\).
(Ces méthodes utilisent le mot sample au lieu de pixel pour des raisons qui deviendront claires plus tard, lors de l'introduction du suréchantillonnage.)
2.4 Tests
Comme d'habitude, nous ne vous fournissons pas de tests unitaires mais un fichier de vérification de noms contenu dans une archive Zip à importer dans votre projet.
3 Résumé
Pour cette étape, vous devez :
- écrire les classes
Summit,GazetteerParseretPanoramaParametersselon les instructions données plus haut, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 24 mars à 16h30, via le système de rendu.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus et aucun retard, aussi insignifiant soit-il, ne sera toléré !
Notes de bas de page
En anglais, le terme gazetteer désigne un index géographique, tandis que le terme parser, très fréquent en informatique, désigne un analyseur syntaxique.
