Aires
ChaCuN – étape 3
1. Introduction
Le but de cette troisième étape est d'écrire les classes permettant de représenter les aires, qui sont des ensembles de zones de même type connectées entre elles.
2. Concepts
2.1. Aires
Lorsque deux tuiles sont placées côte à côte sur le plateau, un des bords de la première touche un des bords de la seconde. Comme nous l'avons vu, ces deux bords doivent être de la même sorte, ce qui implique que les zones des deux tuiles qui touchent leur bord commun se combinent en de plus grandes régions connexes que nous nommerons des aires (areas).
Par exemple, en plaçant côte à côte les tuiles 17, 56 et 27, la zone 0 de la tuile 56 — un pré comportant un auroch — forme une aire avec la zone 2 de la tuile 17 — un pré comportant un cerf. Cela est illustré par l'image ci-dessous, sur laquelle les limites des différentes aires sont mises en évidence en rouge.

Il existe un total de quatre sortes d'aires dans ChaCuN :
- les aires pré, composées de zones pré connectées,
- les aires forêt, composées de zones forêt connectées,
- les aires rivière, composées de zones rivière connectées,
- les réseaux hydrographiques (river systems), composés de zones aquatiques (rivières ou lacs) connectées.
Notez que l'existence des réseaux hydrographiques implique qu'une zone rivière appartient toujours à deux aires : une aire rivière, et un réseau hydrographique.
Les aires sont importantes dans ChaCuN, puisque ce sont elles qui, sous certaines conditions, rapportent des points à leurs occupants majoritaires.
2.1.1. Connexions ouvertes
Une aire possède un certain nombre de connexions ouvertes (open connections), qui sont les segments de bords « libres » que touchent les zones composant l'aire — un bord de tuile étant libre s'il ne touche pas un bord d'une autre tuile. Une aire dont le nombre de connexions ouvertes est supérieur à zéro est dite ouverte (open), tandis qu'une aire dont ce nombre est nul est dite fermée (closed).
L'image ci-dessous montre un plateau constitué de 9 tuiles formant plusieurs aires, dont deux prés. Le plus grand d'entre eux possède un total de dix connexions ouvertes, numérotées de 1 à 10. Notez en particulier que les connexions 5 et 6 correspondent à un seul bord de tuile, mais il s'agit néanmoins de deux connexions distinctes.

De même, toutes les aires visibles sur la figure 1 plus haut sont ouvertes. La forêt a une connexion ouverte, les trois prés comportant des animaux en ont deux chacun, et les deux prés vides — sur les tuiles des extrémités — en ont trois chacun. La rivière connectée au lac a une seule connexion ouverte, de même que le réseau hydrographique qui la contient. Les deux autres rivières — et réseaux hydrographiques correspondant — en ont deux.
Il est possible de fermer la forêt de la figure 1 en rajoutant une tuile au sud de la tuile de départ, comme illustré à la figure 3 ci-dessous.

La distinction entre aires ouvertes et fermées est importante car, comme nous l'avons vu, deux sortes d'aires — les forêts et les rivières — rapportent des points à leurs occupants majoritaires lorsqu'elles sont fermées.
2.1.2. Connexion d'aires
Lorsqu'une nouvelle tuile est posée sur le plateau de jeu, les aires qu'elle contient — ou en tout cas certaines d'entre elles — se retrouvent connectées avec les aires des tuiles adjacentes pour former de nouvelles aires plus grandes.
Conceptuellement, la connexion des aires d'une tuile nouvellement posée avec celles déjà présentes sur le plateau est instantanée. Toutefois, pour bien comprendre le processus, et surtout pour pouvoir correctement le mettre en œuvre, il vaut la peine de le voir comme une séquence de connexions de paires d'aires entre elles.
Pour illustrer cela, imaginons le plateau suivant, constitué de trois tuiles. Les zones de ces tuiles forment un total de quatre aires : 3 prés — que nous ignorerons dans ce qui suit — et une forêt. La forêt comporte à ce stade deux connexions ouvertes : une sur le bord sud de la tuile de droite, et une sur le bord est de la tuile du bas.

Admettons que l'on ajoute maintenant une quatrième tuile dans le coin en bas à droite de ce plateau. Dans un premier temps, on considère que les aires de cette tuile — un pré et une forêt — ne sont pas connectées à celles des tuiles voisines, comme illustré ci-dessous. La forêt de la nouvelle tuile comporte elle aussi deux connexions ouvertes.

Une fois la tuile posée, on procède à la connexion des aires. On peut par exemple commencer par connecter les aires de la nouvelle tuile avec celles de sa voisine ouest. Il en résulte la situation illustrée ci-dessous, où la forêt obtenue par combinaison de celle du plateau et celle de la nouvelle tuile comporte maintenant deux connexions ouvertes — une sur le bord sud de la tuile en haut à droite, et une sur le bord nord de la nouvelle tuile.

Finalement, on peut connecter la nouvelle tuile avec sa voisine du nord, ce qui a pour effet de supprimer les deux dernières connexions ouvertes de la forêt, qui est maintenant fermée. La situation finale est visible dans l'image ci-dessous.

Comme cet exemple l'illustre, suite à la pose d'une tuile sur le plateau, une aire peut être connectée soit à une aire différente — comme lors de la connexion de la nouvelle tuile avec sa voisine ouest — soit à elle-même — comme lors de la connexion de la nouvelle tuile avec sa voisine nord.
Cette différence est importante, entre autres, pour déterminer le nombre de connexions ouvertes de l'aire résultant de la connexion. En effet, lorsqu'une aire est connectée à une aire différente d'elle, le nombre de connexions ouvertes de l'aire résultante est égal à la somme du nombre de connexions ouvertes des deux aires, moins deux — car la connexion a supprimé une connexion ouverte de la première aire, et une de la seconde.
Par contre, lorsqu'une aire est connectée à elle-même, alors le nombre de connexions ouvertes qui restent après cette connexion est simplement le nombre de connexions ouvertes de l'aire, moins deux — pour les mêmes raisons que précédemment.
2.1.3. Occupants
Il a déjà été dit que, lorsqu'un joueur place une nouvelle tuile sur le plateau, il a éventuellement la possibilité d'occuper l'une des zones de cette tuile. Cela n'est toutefois autorisé que si l'aire à laquelle appartient la zone en question n'est pas déjà occupée.
Cela n'implique toutefois pas qu'une aire ne peut être occupée que par un seul occupant ! Il est en effet possible que deux aires disjointes soient occupées individuellement avant de se retrouver connectées par une tuile nouvellement posée, auquel cas l'aire résultante possède plus d'un occupant.
Par exemple, l'image ci-dessous montre 5 tuiles comportant trois aires forêt disjointes, entourées en rouge pour faciliter leur identification. Chacune d'entre elles est occupée par un seul pion, deux d'entre eux appartenant au joueur de couleur jaune, le dernier au joueur de couleur verte.
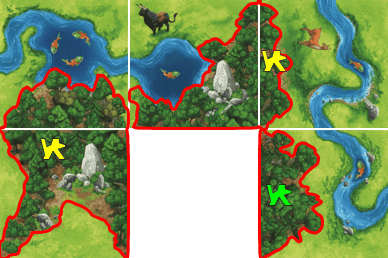
En plaçant une sixième tuile comportant trois bords forêt, il est possible de joindre ces trois aires forêts disjointe en une unique aire forêt occupée par les trois occupants susmentionnés. Cette nouvelle aire, désormais fermée, est entourée sur l'image ci-dessous.
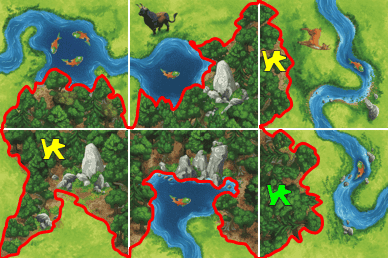
2.2. Partition des zones
Chacune des quatre différentes sortes d'aires forme ce que l'on nomme une partition (partition) de l'ensemble des zones qui lui correspond.
En mathématiques, une partition d'un ensemble \(S\) est un ensemble de sous-ensembles disjoints de \(S\) dont l'union est égale à \(S\). Par exemple, l'ensemble d'ensembles d'entiers \(P\) suivant : \[ P = \{ \{0\}, \{1,3,5,7\}, \{2,4,6\}\} \] est une partition de l'ensemble \(S\) suivant : \[ S = \{0, 1, 2, 3, 4, 5, 6, 7 \} \] En effet, les trois ensembles d'entiers qui constituent \(P\) sont disjoints — aucun entier n'appartient à plus d'un de ces ensembles — et leur union est égale à \(S\).
Si l'on considère, par exemple, l'ensemble de toutes les zones pré des tuiles posées sur le plateau de jeu, il devrait être clair que les aires pré en constituent une partition. En effet, les aires sont disjointes — aucune zone pré n'appartient à plus d'une aire pré — et l'union des zones qui constituent ces aires est égale à l'ensemble de toutes les zones pré.
De la même manière, les aires forêt constituent une partition des zones forêt ; les aires rivière constituent une partition des zones rivière ; et les réseaux hydrographiques constituent une partition des zones aquatiques — rivières et lacs.
3. Mise en œuvre Java
3.1. Enregistrement Area
L'enregistrement Area du paquetage principal, public et immuable, représente une aire. Il est générique et son paramètre de type, nommé Z, est le type des zones constituant l'aire. Il est donc borné par Zone.
Area possède les attributs suivants :
Set<Z> zones, l'ensemble des zones constituant l'aire,List<PlayerColor> occupants, les couleurs des éventuels joueurs occupant l'aire, triés par couleur,int openConnections, le nombre de connexions ouvertes de l'aire.
Notez bien que, malgré son nom, l'attribut occupants ne contient pas une liste de valeurs de type Occupant, mais simplement une liste de (couleur de) joueurs. En effet, la seule information importante au sujet des occupants d'une aire est leur propriétaire, donc le type Occupant ne conviendrait pas ici.
Le constructeur compact d'Area valide l'argument openConnections et lève IllegalArgumentException si celui-ci n'est pas positif ou nul. De plus, pour garantir l'immuabilité de la classe, il copie l'ensemble de zones reçu, ainsi que la liste des occupants, qui est de plus triée par couleur au préalable — voir les conseils de programmation plus bas pour savoir comment faire cela.
Area offre plusieurs méthodes publiques et statiques permettant d'obtenir différentes informations au sujet des différents types d'aires. Ces méthodes sont statiques car elles ne sont définies que pour des types spécifiques d'aires, et il n'est donc pas possible d'en faire des méthodes d'instance.
Par exemple, la première des méthodes ci-dessous, hasMenhir, n'est définie que pour les aires forêt, donc celles ayant le type Area<Zone.Forest>. Malheureusement, Java ne permet pas de définir des méthodes d'instances qui ne seraient disponibles que pour ce type d'aires, et pas les autres. Par contre, il est tout à fait possible de définir une méthode statique prenant en argument une aire de type Area<Zone.Forest>, et c'est donc la solution que nous avons choisie.
Les méthodes statiques de ce genre sont :
static boolean hasMenhir(Area<Zone.Forest> forest), qui retourne vrai si et seulement si la forêt donnée contient au moins un menhir,static int mushroomGroupCount(Area<Zone.Forest> forest), qui retourne le nombre de groupes de champignons que contient la forêt donnée,static Set<Animal> animals(Area<Zone.Meadow> meadow, Set<Animal> cancelledAnimals), qui retourne l'ensemble des animaux se trouvant dans le pré donné mais qui ne font pas partie de l'ensemble des animaux annulés donné — les animaux annulés pouvant p. ex. être des cerfs dévorés par des smilodons,static int riverFishCount(Area<Zone.River> river), qui retourne le nombre de poissons nageant dans la rivière donnée ou dans l'un des éventuels lacs se trouvant à ses extrémités — les poissons d'un lac donné ne devant être comptés qu'une seule fois même dans le cas où un unique lac termine la rivière aux deux bouts,static int riverSystemFishCount(Area<Zone.Water> riverSystem), qui retourne le nombre de poissons nageant dans le réseau hydrographique donné,static int lakeCount(Area<Zone.Water> riverSystem), qui retourne le nombre de lacs du réseau hydrographique donné.
En plus de ces méthodes statiques, Area offre les méthodes publiques suivantes, qui sont, elles, définies pour toutes les sortes d'aires :
boolean isClosed(), qui retourne vrai si et seulement si (ssi) l'aire est fermée,boolean isOccupied(), qui retourne vrai ssi l'aire est occupée par au moins un occupant,Set<PlayerColor> majorityOccupants(), qui retourne l'ensemble des occupants majoritaires de l'aire,Area<Z> connectTo(Area<Z> that), qui retourne l'aire résultant de la connexion du récepteur (this) à l'aire donnée (that),Area<Z> withInitialOccupant(PlayerColor occupant), qui retourne une aire identique au récepteur, si ce n'est qu'elle est occupée par l'occupant donné ; lèveIllegalArgumentExceptionsi le récepteur est déjà occupé,Area<Z> withoutOccupant(PlayerColor occupant), qui retourne une aire identique au récepteur, mais qui comporte un occupant de la couleur donnée en moins ; lèveIllegalArgumentExceptionsi le récepteur ne contient aucun occupant de la couleur donnée,Area<Z> withoutOccupants(), qui retourne une aire identique au récepteur, mais totalement dénuée d'occupants,Set<Integer> tileIds(), qui retourne l'ensemble de l'identité des tuiles contenant l'aire,Zone zoneWithSpecialPower(Zone.SpecialPower specialPower), qui retourne la zone de l'aire qui possède le pouvoir spécial donné, ounulls'il n'en existe aucune.
3.1.1. Conseils de programmation
- Tri des occupants
Le constructeur compact doit trier par couleur la liste des occupants reçue. Cela signifie que les éléments de la liste doivent apparaître dans l'ordre de déclaration des éléments du type énuméré
PlayerColor: les éventuelles occurrences deREDd'abord, suivies des éventuelles occurrences deBLUE, etc.Cela est beaucoup plus simple à garantir qu'il n'y paraît, d'une part car les éléments d'un type énuméré sont comparables — une notion que nous examinerons plus tard au cours mais qui signifie que ces éléments savent se comparer entre eux — et d'autre part car la méthode
sortdeCollectionspermet de trier une liste de valeurs comparables par ordre croissant.L'extrait de code ci-dessous, dont vous pouvez vous inspirer, illustre l'utilisation de ces deux propriétés pour trier une liste de valeurs de type
Direction— le type énuméré défini à l'étape 1 :List<Direction> directions = List.of(Direction.S, Direction.N, Direction.E); List<Direction> sortedDirections = new ArrayList<>(directions); Collections.sort(sortedDirections); System.out.println(sortedDirections); // affiche [N, E, S]
- Méthode
riverFishCount
Une manière d'éviter de compter à deux reprises les poissons d'un lac terminant une rivière aux deux bouts est de stocker les lacs déjà rencontrés dans un ensemble. Il est alors utile de savoir que la méthode
adddes ensembles retourne un booléen, qui est vrai si et seulement si l'élément ajouté ne se trouvait pas encore dans l'ensemble. - Méthode
majorityOccupants
La méthode
majorityOccupantsn'est pas totalement triviale à écrire, et nous vous suggérons donc de la rédiger de la manière suivante.Dans un premier temps, construisez un tableau d'entiers indexé par le nombre ordinal de chaque couleur (0 pour
RED, 1 pourBLUE, etc.) et remplissez-le avec le nombre d'occupants de chaque couleur. Par exemple, si le joueur de couleur rouge possède deux occupants, celui de couleur verte aussi, tandis que celui de couleur bleue n'en possède qu'un, et les autres joueurs aucun, ce tableau est :[2, 1, 2, 0, 0]
Cela fait — ou, mieux encore, au moment de la construction — déterminez le maximum des éléments de ce tableau et, s'il est supérieur à zéro, retournez l'ensemble des couleurs des joueurs possédant ce nombre maximum d'occupants.
- Méthode
connectTo
Lors de l'écriture de la méthode
connectTo, n'oubliez pas que l'aire passée en argument peut être soit une aire différente du récepteur (this), soit la même aire. Or la manière dont le nombre de connexions ouvertes de l'aire résultante est calculé dépend de cela, et il faut donc bien penser à distinguer ces deux cas.
3.2. Enregistrement ZonePartition
L'enregistrement ZonePartition du paquetage principal, publique et immuable, représente une partition de zones d'un type donné — c.-à-d. un ensemble d'aires formant une partition. Tout comme Area, ZonePartition est générique et son paramètre de type, nommé Z et borné par Zone, représente le type des zones de la partition.
Cet enregistrement possède un seul attribut :
Set<Area<Z>> areas, l'ensemble des aires formant la partition.
Bien entendu, pour garantir l'immuabilité de la classe, le constructeur compact de ZonePartition copie l'ensemble d'aires reçu au moyen de la méthode copyOf.
En plus du constructeur primaire, ZonePartition possède un constructeur secondaire qui ne prend aucun argument et initialise la partition avec un ensemble d'aires vide.
Finalement, ZonePartition offre la méthode publique suivante :
Area<Z> areaContaining(Z zone), qui retourne l'aire contenant la zone passée en argument, ou lèveIllegalArgumentExceptionsi la zone n'appartient à aucune aire de la partition.
3.3. Classe ZonePartition.Builder
La classe Builder, imbriquée statiquement dans ZonePartition, publique et finale, sert de bâtisseur à la classe ZonePartition. Tout comme ZonePartition, cette classe est générique, et son paramètre de type, nommé Z, est borné par Zone.
Comme d'habitude, les attributs de ce bâtisseur sont les mêmes que ceux de la classe qu'il construit, mais ils ne sont pas immuables. En d'autres termes, Builder possède comme unique attribut (privé) un ensemble d'aires non immuable, qui est une instance de HashSet<Area<Z>>.
L'unique constructeur de Builder prend en argument une partition de zones existante, de type ZonePartition<Z>, et initialise l'ensemble des aires du bâtisseur avec celui de cette partition. L'idée est que ce constructeur sera utilisé pour créer une partition de zones à partir d'une autre déjà existante.
En plus de ce constructeur, Builder offre les méthodes suivantes dont le but est généralement de modifier, d'une manière ou d'une autre, la partition en cours de construction :
void addSingleton(Z zone, int openConnections), qui ajoute à la partition en cours de construction une nouvelle aire inoccupée, constituée uniquement de la zone donnée et possédant le nombre de connexions ouvertes donné,void addInitialOccupant(Z zone, PlayerColor color), qui ajoute à l'aire contenant la zone donnée un occupant initial de la couleur donnée, ou lèveIllegalArgumentExceptionsi la zone n'appartient pas à une aire de la partition, ou si l'aire est déjà occupée,void removeOccupant(Z zone, PlayerColor color), qui supprime de l'aire contenant la zone donnée un occupant de la couleur donnée, ou lèveIllegalArgumentExceptionsi la zone n'appartient pas à une aire de la partition, ou si elle n'est pas occupée par au moins un occupant de la couleur donnée,void removeAllOccupantsOf(Area<Z> area), qui supprime tous les occupants de l'aire donnée, ou lèveIllegalArgumentExceptionsi l'aire ne fait pas partie de la partition,void union(Z zone1, Z zone2), qui connecte entre elles les aires contenant les zones données pour en faire une aire plus grande ; lèveIllegalArgumentExceptionsi l'une des deux zones n'appartient pas à une aire de la partition,ZonePartition<Z> build(), qui construit la partition de zones.
3.3.1. Conseils de programmation
- Remplacement d'aires
Étant donné que
Areaest immuable,addInitialOccupantn'a pas d'autre choix que de procéder en trois phases : premièrement, trouver l'aire contenant la zone donnée ; deuxièmement, créer une nouvelle aire identique à celle trouvée mais avec l'occupant initial donné ; troisièmement, remplacer dans la partition l'ancienne aire par la nouvelle. Il ne faut surtout pas oublier de supprimer l'ancienne aire de la partition (au moyen de la méthoderemove), faute de quoi il ne s'agit plus d'une partition !Cette manière de procéder est bien entendu aussi valable pour les autres méthodes qui changent une caractéristique d'une (ou plusieurs) aire(s) de la partition.
- Méthode
union
Lors de l'écriture de la méthode
union, souvenez-vous que les deux zones données peuvent appartenir à la même aire.
3.4. Tests
Comme pour l'étape précédente, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures à importer dans votre projet.
4. Résumé
Pour cette étape, vous devez :
- écrire les classes
Area,ZonePartitionetZonePartition.Builderselon les indications donnés plus haut, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 8 mars 2024 à 18h00, au moyen du programme
Submit.javafourni et des jetons disponibles sur votre page privée.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !