L-systèmes
CS-108 — Série 4
Introduction
Le but de cette série est de vous familiariser avec l'utilisation des ensembles et des tables associatives, en les utilisant pour mettre en œuvre les L-systèmes, décrits ci-dessous. Les L-systèmes permettent de générer facilement et élégamment des images dites fractales.
L-Système
Un L-système (ou système de Lindenmayer) est un système de récriture permettant de générer des chaînes de caractères à partir de règles. Un L-système a deux composantes principales :
- une chaîne de départ,
- au moins une règle de récriture.
Les règles décrivent comment faire évoluer, par récriture, la chaîne de départ pour en obtenir une nouvelle, généralement plus longue. Comme nous le verrons plus loin, ces chaînes peuvent ensuite être interprétées comme des instructions de dessin afin de générer des images.
Pour illustrer cette idée, considérons un premier L-système, composé de la chaîne de départ :
F
et d'une unique règle de récriture :
F → F-F++F-F
Cette règle stipule que le caractère F (à gauche de la flèche) doit être récrit en la chaîne F-F++F-F (à droite de la flèche).
Pour faire évoluer ce L-système, on applique simplement la règle de récriture aux caractères de la chaîne de départ. Ce faisant, on obtient pour notre exemple la chaîne suivante :
F-F++F-F
Bien entendu, il est possible de faire évoluer cette chaîne une seconde fois, afin d'obtenir la deuxième évolution du L-système original. Notez que lorsqu'un caractère n'apparaît pas à gauche d'une règle, comme - ou + ici, il est simplement laissé tel quel. Dès lors, seul le caractère F est remplacé dans la chaîne ci-dessus, mais comme il y apparaît quatre fois, la règle est appliquée quatre fois. On obtient alors :
F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F
Et ainsi de suite, autant de fois que l'on désire.
Générer de telles chaînes n'est pas très intéressant en soi. Toutefois, en les interprétant comme des instructions de dessin, on obtient des images qui le sont beaucoup plus.
Interprétation
Une chaîne de caractères produite par un L-système peut être interprétée comme une séquence d'instructions de dessin. Par exemple, on peut attribuer la signification suivante aux caractères F, - et + apparaissant dans les chaînes ci-dessus :
- le caractère
Fsignifie : dessiner un trait dans la direction courante, - le caractère
-signifie : tourner à gauche de 60°, - le caractère
+signifie : tourner à droite de 60°.
En admettant que la direction initiale soit de 0°, donc vers l'est de l'écran, la chaîne F-F++F-F s'interprète ainsi :
- dessiner un trait (
F), - tourner de 60° vers la gauche (
-), c-à-d en direction du nord-est, - dessiner un trait (
F), - tourner de 120° vers la droite (
++), c-à-d en direction du sud-est, - dessiner un trait (
F), - tourner de 60° vers la gauche (
-), c-à-d en direction de l'est, - dessiner un trait (
F).
En suivant ces instructions, on obtient l'image suivante :
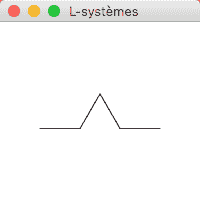
En faisant évoluer ce L-système trois fois encore, on obtient une chaîne qui, interprétée, produit l'image ci-dessous, une fractale connue sous le nom de courbe de Koch :
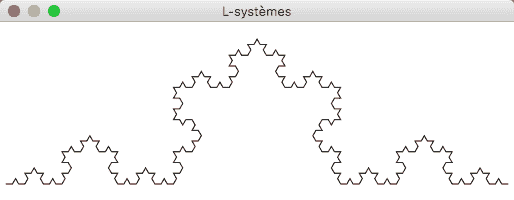
Squelette
Pour faciliter votre travail, nous vous fournissons un squelette de projet dans une archive Zip. Après avoir extrait son contenu, créez un projet à partir du répertoire LSYS qu'elle contient.
L'archive contient :
- les classes
LSystemPainteretTurtle, qui permettent d'interpréter un L-système pour produire une image, - la classe
Main, qui définit un L-système, le transforme en image, et affiche celle-ci à l'écran.
Pour commencer, vous n'avez pas besoin de comprendre le fonctionnement des classes LSystemPainter et Turtle, ni de la classe Main, à l'exception de sa méthode koch et de la première ligne de sa méthode main, qui définit le L-système à dessiner.
Exercice 1 : L-système non évolutif
Pour commencer, définissez un enregistrement immuable nommé LSystem possédant les attributs suivants :
String string, la chaîne de départ du L-système,Map<Character, String> rules, les règles de récriture, représentées par une table associant à chaque caractère à récrire la chaîne en laquelle il doit être récrit — au besoin, examinez la méthodekochde la classeMainpour comprendre comment la règle de récriture donnée plus haut est exprimée au moyen d'une table associative,Set<Character> lineChars, l'ensemble des caractères provoquant le dessin d'une ligne droite — par exemple le caractèreFpour la courbe de Koch,int turningAngle, l'angle de la rotation provoquée par les caractères-et+, en degrés.
Ajoutez ensuite un constructeur compact à l'enregistrement, qui garantisse l'immuabilité de la classe. Finalement, ajoutez-lui un constructeur secondaire prenant les mêmes arguments que le constructeur principal défini automatiquement par Java, sauf lineChars qui est passé, dans cette version, sous la forme d'une chaîne de caractères.
Ce constructeur secondaire a pour but de faciliter l'utilisation de la classe, et convertit simplement la chaîne lineChars en l'ensemble de caractères correspondant. Par exemple, il transforme la chaîne ABC en l'ensemble de trois caractères A, B et C.
Notez que pour définir ce constructeur secondaire, vous devez ajouter une méthode statique privée à LSystem, qui se charge de la conversion d'une chaîne en un ensemble. En effet, Java n'autorise pas un constructeur secondaire à contenir du code avant l'appel au constructeur primaire — qui est fait avec la notation this(…).
Une fois le constructeur et les méthodes ci-dessus définis, vous devriez être capable d'obtenir l'image de la figure 1 plus haut en définissant la variable lSystem de la méthode main ainsi :
LSystem lSystem = new LSystem("F-F++F-F", Map.of(), "F", 60);
Bien entendu, ce L-système n'est pas très intéressant car il ne possède aucune règle, mais il permet de vérifier que tout est en place pour l'exercice suivant.
Exercice 2 : L-système évolutif
Terminez l'enregistrement LSystem en lui ajoutant les deux variantes suivantes d'une méthode nommée evolve :
public LSystem evolve() { /* à faire */ }
public LSystem evolve(int steps) { /* à faire */ }
Commencez par la variante sans arguments, qui retourne la version évoluée une fois du L-système auquel on l'applique. Ce nouveau L-système a les mêmes attributs que celui auquel on l'applique, à l'exception de la chaîne de départ, qui est le résultat d'une étape d'évolution — donc d'une et une seule application des règles — de la chaîne de départ du L-système original.
Une fois la première variante de la méthode evolve terminée, écrivez la seconde, qui applique la première un certain nombre de fois et retourne le L-système final.
Vérifiez que vos méthodes d'évolution fonctionnent en définissant la variable lSystem de la méthode main ainsi :
LSystem lSystem = koch().evolve(4);
et en comparant l'image obtenue à celle de la figure 2.
Exercice 3 : flocon de Koch
La méthode koch qui vous est fournie permet de générer la courbe de Koch illustrée plus haut. En modifiant uniquement la chaîne de départ du L-système, arrivez-vous à dessiner le flocon de Koch, montré ci-dessous après 4 itérations ?

Exercice 4 : L-systèmes divers
Utilisez votre classe LSystem pour modéliser et dessiner les L-systèmes décrits ci-dessous. Contrairement à celui de la courbe de Koch, ces L-systèmes ont souvent plus d'une règle, et parfois une chaîne de départ composée de plus d'un caractère.
Attention : certains de ces systèmes produisent très vite des chaînes énormes, commencez donc toujours par un petit nombre d'évolutions (4 ou 5).
Triangle de Sierpinski
Le triangle de Sierpinski a pour chaîne de départ A, pour angle de rotation 60°, pour caractères de dessin A et B et pour règles :
A → +B-A-B+ B → -A+B+A-
Courbe de Hilbert
La courbe de Hilbert a pour chaîne de départ A, pour angle de rotation 90°, pour caractère de dessin F et pour règles :
A → -BF+AFA+FB- B → +AF-BFB-FA+
Courbe du dragon
La courbe du dragon a pour chaîne de départ FX, pour angle de rotation 90°, pour caractère de dessin F et pour règles :
X → X+YF+ Y → -FX-Y
Exercice 5 : L-systèmes avec sauvegarde du contexte
Pour pouvoir dessiner les deux derniers L-Systèmes de cette série, il vous faut augmenter au préalable la classe LSystemPainter.
La méthode paint de cette classe se charge de transformer la chaîne d'un L-système en un dessin. Pour ce faire, elle utilise ce qu'on appelle souvent une « tortue » (turtle), chargée d'effectuer le dessin. L'idée est que la tortue pointe toujours dans une direction donnée, et que chaque fois qu'on lui demande de bouger, elle avance tout droit dans cette direction d'une distance fixe, en laissant une trace sur le sol. Il est aussi possible de lui demander de se tourner, auquel cas la direction dans laquelle elle pointe change.
La méthode paint de LSystemPainter interprète les caractères de la chaîne d'un L-système en commandes pour la tortue : si le prochain caractère est + ou - alors elle tourne la tortue de l'angle de rotation du L-système dans un sens ou dans l'autre, tandis que s'il s'agit d'un caractère de dessin, alors elle fait avancer la tortue.
Tous les L-systèmes définis jusqu'à présent n'utilisaient que ces deux opérations (rotation et avancement) et votre but est d'en ajouter maintenant deux nouvelles : la sauvegarde et la restauration de la tortue.
Pour ce faire, il vous faut ajouter une pile à votre méthode paint, capable de stocker des tortues, c.-à-d. des instances de Turtle. La sauvegarde de la tortue, représentée par le caractère [, place simplement la tortue actuelle (stockée dans la variable t) au sommet de cette pile. La restauration de la tortue, représentée par le caractère ], retire la tortue qui se trouve au sommet de la pile et l'utilise comme nouvelle tortue en la stockant dans la variable t. Ce faisant, elle doit également effectuer l'appel suivant :
p.moveTo(t.x(), t.y());
dans le but de garantir que le prochain trait dessiné par la tortue débutera effectivement à la position de la tortue restaurée.
Les modifications à apporter à la méthode paint sont très courtes : une ligne pour déclarer et créer la pile des tortues, et deux nouveaux cas dans le switch pour gérer les caractères [ et ]. Le premier cas tient en une seule ligne, le second en deux en raison de l'appel à moveTo susmentionné.
Une fois les modifications apportées à la méthode paint, testez-les au moyen des deux derniers L-systèmes ci-dessous, qui utilisent les nouveaux caractères.
Arbre
L'arbre a pour chaîne de départ ----F, pour angle de rotation 25°, pour caractère de dessin F et pour règle :
F → FF+[+F-F-F]-[-F+F+F]
Plante
La plante a pour chaîne de départ ---X, pour angle de rotation 30°, pour caractère de dessin F et pour règles :
X → F-[[X]+X]+F[+FX]-X F → FF