Messages d'identification et de position
Javions – étape 5
1. Introduction
Le but principal de cette cinquième étape est d'écrire des classes représentant deux types de messages ADS-B : les messages d'identification, et les messages de positionnement en vol.
2. Concepts
2.1. Messages d'identification
Les messages d'identification et de catégorie (aircraft identification and category) permettent aux aéronefs de communiquer leur indicatif et leur catégorie.
Les messages d'identification ont un code de type valant 1, 2, 3 ou 4, stocké pour mémoire dans les 5 bits de poids fort de l'attribut ME du message. Le contenu des 51 autres bits de cet attribut est donné par la table suivante :
| Nom | Début | Bits | Contenu |
|---|---|---|---|
CA |
48 | 3 | Catégorie de l'aéronef (partielle) |
C1 |
42 | 6 | Premier caractère de l'indicatif |
C2 |
36 | 6 | Second caractère de l'indicatif |
C3 |
30 | 6 | Troisième caractère de l'indicatif |
C4 |
24 | 6 | Quatrième caractère de l'indicatif |
C5 |
18 | 6 | Cinquième caractère de l'indicatif |
C6 |
12 | 6 | Sixième caractère de l'indicatif |
C7 |
6 | 6 | Septième caractère de l'indicatif |
C8 |
0 | 6 | Huitième caractère de l'indicatif |
(Notez bien que cette table liste les champs en commençant par ceux se trouvant dans les bits de poids fort de ME, car cela correspond au sens de lecture habituel.)
La catégorie de l'aéronef donne une indication sur son type — avion, hélicoptère, ballon, etc. — ainsi que sur sa taille. Cette catégorie est obtenue en combinant les trois bits du champ CA avec le code de type du message, qui pour mémoire peut valoir 1, 2, 3 ou 4. Ces deux valeurs sont combinées en une seule valeur de 8 bits dont les 4 bits de poids fort valent 14 moins le code de type, et les 4 bits de poids faible sont le champ CA. Par exemple, un aéronef envoyant un message d'identification et de catégorie dont le code de type vaut 4 et le champ CA vaut 3 appartient à la catégorie A316.
L'indicatif (call sign) est une séquence de 8 caractères, chacun d'entre eux étant représenté au moyen d'un entier de 6 bits et pouvant être :
- une des 26 lettres majuscules et non accentuée de l'alphabet latin (
AàZ), représentées par les entiers allant de 1 (inclus) à 26 (inclus), - un des 10 chiffres décimaux (
0à9), représentés par les entiers allant de 48 (inclus) à 57 (inclus), - l'espace, représentée par l'entier 32.
Les 27 entiers ne représentant pas de caractères — p. ex. 0 ou ceux de la plage allant de 27 à 31 — sont invalides et ne devraient jamais figurer dans un message. En particulier, on notera que lorsqu'un indicatif est plus court que 8 caractères, les caractères inutilisés sont transmis comme des espaces en fin d'indicatif, qui sont ignorés par la suite.
Pour les avions de ligne, les 3 premières lettres de l'indicatif identifient généralement l'opérateur du vol. Par exemple, un des indicatifs utilisé par l'avion immatriculé HB-JDC présenté à l'étape 2 est SWR32CH. Les trois premières lettres (SWR) identifient la compagnie Swiss.
2.2. Messages de positionnement en vol
Les messages de positionnement en vol (airborne position) permettent aux aéronefs de transmettre leur position lorsqu'ils sont en vol, composée de leur longitude, latitude et altitude.
Ces messages ont un code de type compris soit entre 9 (inclus) et 18 (inclus), soit entre 20 (inclus) et 22 (inclus). Le contenu des 51 autres bits de leur attribut ME est donné par la table suivante — à l'exception de celui des 3 bits de poids fort, qui contiennent des attributs inutilisés dans ce projet :
| Nom | Début | Bits | Contenu |
|---|---|---|---|
ALT |
36 | 12 | Altitude |
TIME |
35 | 1 | inutilisé dans ce projet |
FORMAT |
34 | 1 | Format du message (0 : pair, 1 : impair) |
LAT_CPR |
17 | 17 | Latitude « compacte » (locale) |
LON_CPR |
0 | 17 | Longitude « compacte » (locale) |
Le décodage de ces attributs n'est pas simple, et les sections qui suivent expliquent la marche à suivre.
2.2.1. Décodage de la longitude et de la latitude
Dans un message de positionnement en vol, 17 bits sont réservés à la longitude, et 17 autres à la latitude. Cela n'est pas beaucoup, et si la longitude était effectivement représentée uniquement au moyen de ces 17 bits, la précision à l'équateur ne serait que de 300 m environ, ce qui n'est pas suffisant pour le contrôle aérien.
Dès lors, la longitude et la latitude sont transmises en utilisant une technique assez subtile — nommée compact position reporting (CPR) en anglais — et qui permet, en combinant les informations de deux messages successifs, d'obtenir une précision de l'ordre de 5 m.
Pour comprendre l'idée de cette technique, il peut être utile de considérer un cas plus simple, celui de la représentation de la position d'un point se déplaçant le long d'une ligne droite.
2.2.2. Position le long d'une ligne
Imaginons que l'on désire représenter au moyen de 3 bits la position d'un point se trouvant sur une droite de 12 cm.
Une technique évidente consiste à découper la droite en 8 (23) segments de 1.5 cm chacun, et à représenter la position du point par l'index du segment dans lequel il se trouve, compris entre 0 et 7. Cette idée est illustrée sur la figure ci-dessous, qui montre la ligne découpée en 8 segments et le point P dont on désire représenter la position, qui se trouve dans le segment 3.

Si le point ne bouge pas, cette représentation convient très bien. Toutefois, si le point se déplace lentement le long de la ligne, elle ne semble pas optimale. En effet, dans ce cas, dès qu'on connaît la position du point à un instant donné, on sait que sa position à l'instant prochain n'en sera pas trop éloignée. Il serait donc bien de pouvoir tirer parti de cela pour utiliser les 3 bits à notre disposition de manière plus judicieuse que celle suggérée ci-dessus.
Une première idée serait de découper la ligne en 4 zones de 3 cm, et d'utiliser les 3 bits pour représenter la position locale du point dans la zone dans laquelle il se trouve, plutôt que de les utiliser pour représenter sa position globale comme précédemment. Cela représente un gain en précision d'un facteur 4, mais suppose bien entendu de connaître, d'une manière ou d'une autre, la zone dans laquelle le point se trouve. Sans cette information, la position est ambiguë, puisqu'à chaque position locale correspondent 4 positions globales possibles.
Cette idée est illustrée dans la figure ci-dessous, qui montre la droite découpée en 4 zones (en rouge), chacune découpée en 8 secteurs — seuls ceux de la zone contenant le point sont illustrés, pour alléger la présentation. Le point P est dans le secteur 6 de sa zone, qui porte elle le numéro 1. Bien entendu, sans savoir dans laquelle des 4 zones P se trouve, sa position est ambiguë, ce qui est illustré par les points gris montrant les autres positions que P pourrait occuper.
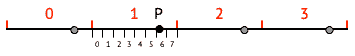
Pour lever cette ambiguïté, on peut introduire un second découpage de la ligne, utilisant cette fois 3 zones de 4 cm chacune (en bleu), puis représenter une fois encore la position locale du point dans sa zone au moyen des 3 bits à notre disposition. Ce second découpage est illustré dans la figure ci-dessous, et on constate que le point P se trouve ici dans le secteur 2 de sa zone, qui porte à nouveau le numéro 1.
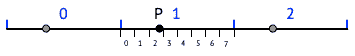
Là aussi, le simple fait de connaître la position locale du point P dans sa zone ne suffit pas à déterminer sans ambiguïté sa position globale, puisqu'il y a maintenant 3 possibilités.
Toutefois, en combinant les deux positions locales, celle dans le découpage en 4 zones et celle dans le découpage en 3 zones, on peut déterminer sans ambiguïté la position globale du point. Il est aisé de vérifier cela visuellement, en constatant que parmi les quatre positions possibles dans le premier découpage, il n'y en a qu'une qui correspond à l'une des trois positions possibles dans le second.
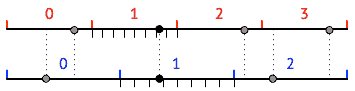
Plutôt que d'aligner ainsi visuellement les positions possibles pour déterminer laquelle est la bonne, on peut calculer directement l'index de la zone dans laquelle se trouve le point. Pour cela, il faut à nouveau découper la droite, cette fois en 12 (3×4) « micro-zones » de taille égale, afin que chaque zone du découpage en 4 (rouge) contienne exactement 3 micro-zones, tandis que chaque zone du découpage en 3 (bleu) en contienne exactement 4. La figure ci-dessous illustre cela.

Comme on le constate sur cette figure, les zones d'index 0 sont alignées dans les deux découpages, celles d'index 1 sont décalées d'une micro-zone, tandis que celles d'index 2 sont décalées de deux micro-zones. De manière générale, le début de la zone d'index \(i\) du découpage en 3 est décalé à droite de \(i\) micro-zones par rapport à celui de la zone d'index \(i\) du découpage en 4.
En d'autres termes, si on sait dans laquelle des micro-zone de sa zone le point se trouve pour chacun des découpages, on peut en déterminer l'index de la zone dans laquelle il se trouve par une simple soustraction. Or on connaît la position locale du point dans sa zone, et une division nous permet donc de connaître l'index de la micro-zone correspondante.
Ainsi, dans la figure ci-dessus, le point se trouve dans la micro-zone d'index 3 de sa zone dans le découpage en 4 (rouge), et dans celle d'index 2 dans le découpage en 3 (bleu). Par soustraction de ces deux valeurs (3-2), on en déduit que le point se trouve dans la zone d'index 1 !
Pour résumer, en combinant deux positions locales du point, la première exprimée dans un découpage en 4 zones, la seconde exprimée dans un découpage en 3 zones, on peut déterminer la position globale du point.
Bien entendu, si le point était stationnaire, rien de cela n'aurait le moindre intérêt. Le gros avantage de cette technique est qu'elle fonctionne également lorsque le point se déplace, pour peu que la distance séparant deux positions successives ne soit pas supérieure à celle d'une micro-zone.
2.2.3. Position au voisinage de la Terre
La technique utilisée pour représenter la position d'un aéronef dans un message ADS-B de positionnement en vol est similaire à celle décrite à la section précédente, mais plus complexe pour deux raisons :
- la description d'une position nécessite désormais deux dimensions — longitude et latitude — plutôt qu'une seule,
- le découpage en zones de taille régulière est plus difficile à faire dans le cas de la longitude, car la surface couverte par les 360° de longitude est plus grande à proximité de l'équateur qu'à proximité des pôles.
Pour cette raison, le nombre de zones utilisées pour découper la longitude est variable, et est plus grand à l'équateur qu'aux pôles.
Le nombre de zones utilisée pour découper la latitude est par contre fixe, et vaut alternativement 60 et 59. C'est-à-dire que les messages ADS-B de positionnement en vol transmettent la latitude locale exprimée alternativement dans un découpage dit pair (even) contenant 60 zones, et dans un découpage dit impair (odd) contenant 59 zones.
Les deux constantes ci-dessous donnent le nombre de zones de latitudes utilisées par chacun de deux découpages, le pair étant identifié par l'index 0, l'impair par l'index 1.
\[ Z_{\phi,0} = 60,\hspace{1em} Z_{\phi,1} = 59 \]
L'inverse de ces deux constantes donne la « largeur » des zones, exprimées en tours :
\[ \delta_{\phi,0} = \frac{1}{Z_{\phi,0}},\hspace{1em} \delta_{\phi,1} = \frac{1}{Z_{\phi,1}} \]
Le nombre de zones de longitude utilisées dans le découpage pair dépend de la latitude \(\phi\) et est donnée par la formule suivante :
\[ Z_{\lambda,0} = \left\lfloor \frac{2\pi}{A} \right\rfloor, \textrm{avec } A = \arccos\left(1 - \frac{1 - \cos 2\pi\,\delta_{\phi,0}}{\cos^2 \phi}\right) \]
où \(\lfloor\cdot\rfloor\) représente l'arrondi par défaut (floor en anglais). Cette formule vaut 59 à l'équateur, et n'est pas définie proche des pôles, lorsque la valeur passée à la fonction \(\arccos\) est supérieur à 1 en valeur absolue. Dans ce cas, par définition, \(Z_{\lambda,0} = 1\).
Le nombre de zones de longitude utilisées dans le découpage impair est comme d'habitude donné simplement par :
\[ Z_{\lambda,1} = Z_{\lambda,0} - 1 \]
Chaque zone de longitude et de latitude est découpée en 217 segments, et la position locale de l'aéronef dans la zone qu'il occupe est donc représentée au moyen de 17 bits par coordonnée. Les deux valeurs de 17 bits correspondantes sont transmises dans les attributs LON_CPR et LAT_CPR des messages ADS-B de positionnement en vol.
Comme dans la section précédente, la zone dans laquelle se trouve l'aéronef n'est pas transmise explicitement, mais on peut la calculer au moyen d'une position locale exprimée dans le découpage pair, et d'une position locale exprimée dans le découpage impair.
Nous noterons \(y_0\) la latitude locale de l'aéronef dans le découpage pair, et \(y_1\) sa latitude locale dans le découpage impair. Pour faciliter les calculs, ces valeurs sont normalisées afin d'être comprises entre 0 et 1, où 0 représente le bord sud de la zone, et 1 représente son bord nord. Cette normalisation consiste simplement à interpréter dans un premier temps les 17 bits de l'attribut LAT_CPR d'un message ADS-B comme une valeur entière non signée, puis à la diviser par 217.
Au moyen des valeurs \(y_0\) et \(y_1\), on peut déterminer \(z_{\phi,0}\) et \(z_{\phi,1}\), qui sont les numéros de zone de latitude dans lequel l'aéronef se trouve dans chacun des deux découpages, au moyen de la formule suivante :
\begin{align} z_\phi &= \left[\,y_0\,Z_{\phi,1} - y_1\,Z_{\phi,0}\,\right]\\[0.5em] z_{\phi, i} &= \begin{cases} z_\phi + Z_{\phi, i} & \textrm{si } z_\phi < 0\\ z_\phi & \textrm{sinon} \end{cases}\\[0.5em] \end{align}où \([\cdot]\) représente l'arrondi à l'entier le plus proche.
Cela fait, on peut déterminer la latitude à laquelle l'aéronef se trouvait au moment de l'envoi de chacun des deux messages, notée \(\phi_i\) :
\[ \phi_i = \delta_{\phi,i}\times\left(z_{\phi,i} + y_i\right) \]
Attention, la latitude produite par cette formule est exprimée en tours, et pas en radians ou en degrés, car les constantes \(\delta_{\phi,i}\) sont exprimées dans cette unité. De plus, elle est toujours positive, ce qui ne gêne pas pour les calculs mais n'est pas conforme aux conventions, qui veulent que la latitude soit toujours comprise entre -90° et +90°. Ce problème sera réglé ultérieurement.
Connaissant maintenant la latitude de chacun des deux messages, on peut déterminer le nombre de zones de longitude dans le découpage pair, \(Z_{\lambda,0}\), au moyen de la formule donnée plus haut.
Sachant qu'on a à disposition deux messages, cette formule peut être calculée avec deux latitudes différentes. Si on obtient ainsi deux valeurs différentes, cela signifie qu'entre les deux messages, l'aéronef a changé de « bande de latitude », et il n'est donc pas possible de déterminer sa position. Cette situation devrait néanmoins être rare.
Une fois le nombre de zones de longitude connu, on distingue deux cas pour déterminer la longitude correspondante. Le premier cas est celui où \(Z_{\lambda,0} = 1\), qui correspond aux zones polaires dans lesquelles il n'y a qu'une seule zone de longitude. La longitude est alors donnée simplement par :
\[ \lambda_i = x_i \]
Hors des zones polaires, c.-à-d. lorsque \(Z_{\lambda,0} > 1\), on doit comme pour la latitude calculer les index de zones correspondant aux deux messages :
\begin{align} z_\lambda &= \left[\,x_0\,Z_{\lambda,1} - x_1\,Z_{\lambda,0}\,\right]\\[0.5em] z_{\lambda, i} &= \begin{cases} z_\lambda + Z_{\lambda, i} & \textrm{si } z_\lambda < 0\\ z_\lambda & \textrm{sinon} \end{cases}\\[0.5em] \end{align}grâce auxquels on peut finalement déterminer la longitude :
\[ \lambda_i = \delta_{\lambda,i}\times\left(z_{\lambda,i} + x_i\right), \textrm{avec } \delta_{\lambda,i} = \frac{1}{Z_{\lambda,i}} \]
Tout comme la latitude, cette longitude est exprimée en tours, et est aussi toujours positive.
À ce stade, on connaît donc la longitude et la latitude de l'aéronef lorsqu'il a envoyé chacun des deux messages consécutifs, le pair et l'impair. En général, seule la position correspondant au plus récent des deux nous intéresse. Pour l'obtenir, il faut encore prendre garde à deux caractéristiques des longitudes et latitudes calculées par les formules ci-dessus, déjà mentionnées :
- elles sont exprimées en tours, ce qui n'est pas forcément l'unité que l'on désire utiliser finalement, donc une conversion peut être nécessaire,
- elles sont toujours positives, ce qui est contraire aux conventions, et il faut donc les recentrer autour de 0 en convertissant les angles supérieurs ou égaux à ½ tour en leur équivalent négatif.
2.2.4. Exemple
Afin d'illustrer les calculs de la section précédente, voyons comment les utiliser pour déterminer la position d'un aéronef ayant envoyé successivement deux messages ADS-B de positionnement aérien dont les attributs LON_CPR, LAT_CPR et FORMAT, interprétés comme des entiers non signés, sont :
LON_CPR |
LAT_CPR |
FORMAT |
|---|---|---|
| 111600 | 94445 | 0 |
| 108865 | 77558 | 1 |
Tous les calculs ci-dessous ont été effectués avec des valeurs de type double, mais pour alléger la présentation, leurs résultats sont toujours présentés arrondis à 6 décimales.
La première opération à effectuer consiste à obtenir les deux latitudes normalisées, \(y_0\) et \(y_1\), en divisant les deux attributs LAT_CPR par 217 :
\[ y_0 = 94445\times 2^{-17} \approx 0.720558,\ \ y_1 = 77558\times 2^{-17} \approx 0.591721 \]
Cela nous permet de déterminer les numéros de zones de latitude dans lequel l'aéronef se trouvait dans chacun des deux découpages :
\begin{align} z_\phi &= \left[ 0.720558\times 59 - 0.591721\times 60 \right] = 7\\ z_{\phi,0} &= z_{\phi,1} = 7 \end{align}On en déduit les latitudes auxquelles il se trouvait lors de l'envoi de chacun des messages :
\begin{align} \phi_0 &= \tfrac{1}{60}\times\left(7 + 0.720558\right) \approx 0.128676\,\textrm{turn} \approx 46.323349°\\ \phi_1 &= \tfrac{1}{59}\times\left(7 + 0.591721\right) \approx 0.128673\,\textrm{turn} \approx 46.322363° \end{align}Ces valeurs nous permettent de calculer le nombre de zones de longitude dans le découpage pair correspondant à chacune de ces latitudes. Pour la première, on obtient :
\begin{align} A &= \arccos\left(1 - \frac{1 - \cos 2\pi\,\tfrac{1}{60}}{\cos^2 46.323349°}\right) \approx 0.151715\\ Z_{\lambda,0} &= \left\lfloor \frac{2\pi}{A} \right\rfloor = 41\\ Z_{\lambda,1} &= Z_{\lambda,0} - 1 = 40 \end{align}Pour la seconde latitude, on obtient les mêmes valeurs, ce qui indique que cette paire de messages nous permettra effectivement de déterminer la position de l'aéronef.
On poursuit donc les calculs pour calculer la longitude, en effectuant les mêmes opérations que pour la latitude. On commence par normaliser les positions :
\[ x_0 = 111600\times 2^{-17} \approx 0.851440,\ \ x_1 = 108865\times 2^{-17} \approx 0.830574 \]
puis on calcule les numéros de zones de longitude :
\begin{align} z_\lambda &= \left[ 0.851440\times 40 - 0.830574\times 41 \right] = 0\\ z_{\lambda,0} &= z_{\lambda,1} = 0 \end{align}et finalement les longitudes correspondantes :
\begin{align} \lambda_0 &= \tfrac{1}{41}\times\left(0 + 0.851440\right) \approx 0.020767\,\textrm{turn} \approx 7.476062°\\ \lambda_1 &= \tfrac{1}{40}\times\left(0 + 0.830574\right) \approx 0.020764\,\textrm{turn} \approx 7.475166° \end{align}Si le message le plus récent des deux était le pair, alors la position de l'aéronef au moment de son envoi était :
\[ (\lambda, \phi) = (\lambda_0, \phi_0) = (7.476062°, 46.323349°) \]
2.2.5. Décodage de l'altitude
L'altitude à laquelle se trouve l'aéronef est stockée dans les 12 bits de l'attribut ALT. On pourrait espérer que son décodage soit plus simple que celui de la longitude et de la latitude, mais malheureusement, pour des questions historiques, ce n'est pas vraiment le cas. En effet, l'altitude peut être encodée de deux manières différentes, distinguées par la valeur du bit d'index 4 de l'attribut ALT, nommé Q. Les deux cas sont décrits ci-dessous.
- Cas
Q= 1
Lorsque
Qvaut 1, les 11 bits restants, interprétés comme un entier non signé, donnent l'altitude en multiples de 25 pieds, qui doit être ajoutée à une altitude de base de -1000 pieds.Par exemple, si les 12 bits du champ contenant l'altitude valent
100010110011, alorsQ(en rose) vaut 1, et les 11 bits restants après sa suppression sont10001010011, ce qui correspond à 1107. L'altitude représentée est donc :\[ -1\,000 + 1\,107\times 25 = 26\,675\,\textrm{ft} = 8\,130.54\,\textrm{m} \]
- Cas
Q= 0
Lorsque
Qvaut 0, les 12 bits nécessitent un décodage plus complexe, qui se fait en trois étapes : premièrement, les bits sont « démêlés » et séparés en deux groupes, puis ils sont interprétés comme des codes de Gray — concept décrit à la §2.3 plus bas — et enfin l'altitude est calculée.La première étape, dite de démêlage, consiste à permuter l'ordre des bits afin de faciliter leur interprétation ultérieure. Pour spécifier la permutation à effectuer, les 12 bits sont découpés ci-dessous en 4 groupes de 3 bits, les groupes étant nommés de A à D, et les bits individuels numérotés 1, 2 et 4. Initialement, les 12 bits sont ordonnés de la manière suivante :
C1 A1 C2 A2 C4 A4 B1 D1 B2 D2 B4 D4
et le but du démêlage est de les permuter afin qu'ils soient ordonnés ainsi :
D1 D2 D4 A1 A2 A4 B1 B2 B4 C1 C2 C4
Il faut noter que le bit nommé
D1ci-dessus n'est autre que le bit Q, qui vaut 0. Dès lors, après démêlage, le bit de poids le plus fort vaut toujours 0.Une fois les bits démêlés, ils sont séparés en deux groupes : les trois bits de poids faible, qui encodent les multiples de 100 pieds, et les neuf bits de poids fort, qui encodent les multiples de 500 pieds.
Chacun de ces deux groupes est interprété comme un code de Gray, après quoi le groupe des bits de poids faible subit une dernière transformation.
Premièrement, si sa valeur est 0, 5 ou 6, alors l'altitude est invalide.
Deuxièmement, si la valeur représentée par le groupe des bits de poids faible vaut 7, elle est remplacée par 5.
Troisièmement, si la valeur représentée par le groupe des bits de poids fort (!) est impaire, alors celle représentée par le groupe des bits de poids faible est « reflétée », c.-à-d. remplacée par 6 moins sa valeur originale — 1 devient 5, 2 devient 4, 3 ne change pas, 4 devient 2, et 5 devient 1.
Finalement, l'altitude est calculée en ajoutant à une altitude de base de -1300 pieds les multiples de 100 pieds (multipliés par 100) et les multiples de 500 pieds (multipliés par 500).
Pour illustrer ce décodage complexe, imaginons que les 12 bits du champ contenant l'altitude valent
011001001010, alors Q (en rose) vaut 0. Après démêlage, on obtient000101011010.Les neuf bits de poids fort (
000101011) sont le code de Gray pour la valeur 50 (paire), tandis que les trois bits de poids faible (010) sont le code de Gray pour la valeur 3. Étant donné que cette valeur n'est pas égale à 7, et que le groupe de poids fort représente une valeur paire, l'interprétation du groupe de poids faible ne change pas. On peut donc finalement calculer l'altitude ainsi :\[ -1\,300 + 3\times 100 + 50\times 500 = 24\,000\,\textrm{ft} = 7\,315.2\,\textrm{m} \]
2.3. Code de Gray
Dans la représentation binaire usuelle des nombres, le nombre de bits qui diffèrent entre deux nombres successifs varie. On peut le voir dans la table suivante, qui montre la représentation binaire des nombres compris entre 0 et 7 au moyen de 3 bits, ainsi que le code de Gray correspondant, décrit plus bas.
| Nombre | Binaire | Gray |
|---|---|---|
| 0 | 000 |
000 |
| 1 | 001 |
001 |
| 2 | 010 |
011 |
| 3 | 011 |
010 |
| 4 | 100 |
110 |
| 5 | 101 |
111 |
| 6 | 110 |
101 |
| 7 | 111 |
100 |
On constate ainsi qu'entre la représentation binaire de 0 et de 1, un seul bit change ; entre la représentation de 1 et de 2, deux bits changent ; et entre la représentation de 3 et de 4, les trois bits changent ; etc.
Le fait qu'un nombre important — et variable — de bits change entre deux nombres successifs est parfois problématique. Ainsi, si une valeur est lue par un capteur et que celui-ci lit un bit de manière incorrect, il est possible que la valeur lue soit totalement différente — un 0 peut être lu comme un 4 si le bit de poids fort est lu de manière incorrecte.
Pour cette raison, il peut être intéressant d'avoir une manière d'encoder les nombres qui garantisse qu'un seul bit change entre la représentation d'un nombre et celle de ses deux voisins. Le code de Gray (réfléchi) (reflected Gray code), du nom de son inventeur, est un tel code. On constate ainsi dans la table ci-dessus que dans la colonne intitulée Gray, un seul bit change entre la représentation d'un nombre et ses deux voisins, et cette propriété est vraie même si on considère que la table est circulaire et que 0 et 7 sont voisins.
2.3.1. Construction
La construction du code de Gray est remarquablement simple et élégante. Pour un bit, il est identique au code binaire standard, c'est-à-dire que 0 est représenté par un unique bit valant 0, et 1 est représenté par un unique bit valant 1. Ce code trivial est présenté dans la table ci-dessous :
| Nombre | Encodage |
|---|---|
| 0 | 0 |
| 1 | 1 |
Pour obtenir un code de Gray avec plus de bits, il suffit de partir de ce code-là et d'effectuer les opérations suivantes autant de fois que nécessaire :
- effectuer une réflexion (symétrie) verticale du code — voir plus bas,
- ajouter un 0 en tête du code original, et un 1 en tête du code réfléchi.
Ainsi, à partir du code de Gray à 1 bit, on peut obtenir le code à 2 bits de la manière illustrée dans la table ci-dessous, les bits rouges étant ceux ajoutés en tête du code original et de sa version réfléchie, la ligne noire les séparant représentant l'axe de symétrie :
| Nombre | Encodage |
|---|---|
| 0 | 00 |
| 1 | 01 |
| 2 | 11 |
| 3 | 10 |
En répétant les mêmes opérations sur ce code de Gray à 2 bits, on obtient celui à 3 bits :
| Nombre | Encodage |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 011 |
| 3 | 010 |
| 4 | 110 |
| 5 | 111 |
| 6 | 101 |
| 7 | 100 |
et ainsi de suite.
Il devrait être clair que le code de Gray garantit par construction que les valeurs voisines diffèrent d'exactement un bit.
2.3.2. Décodage
Comme nous l'avons vu, il arrive dans certains car que l'altitude transmise par les aéronefs dans les messages ADS-B soit représentée au moyen d'un code de Gray. Pour décoder cette altitude, on doit donc savoir comment déterminer la valeur binaire \(B\) correspondant à une « valeur de Gray » \(G\) de \(n\) bits, ce qui peut se faire au moyen de la formule suivante :
\[ B = \bigoplus_{i=0}^{n - 1} G \gg i \]
où le symbole \(\oplus\) représente le ou bit-à-bit exclusif — noté ^ en Java — et \(\gg\) le décalage à droite — noté >> en Java.
Par exemple, la valeur binaire correspondant à la « valeur de Gray » 110, s'obtient ainsi :
On en conclut que 110 est la représentation de 1002, soit 4, ce qui est correct d'après la table plus haut.
3. Mise en œuvre Java
3.1. Classe CprDecoder
La classe CprDecoder du sous-paquetage adsb, publique et non instanciable, représente un décodeur de position CPR. Elle ne possède qu'une seule méthode publique, et bien entendu statique :
GeoPos decodePosition(double x0, double y0, double x1, double y1, int mostRecent), qui retourne la positon géographique correspondant aux positions locales normalisées données —x0ety0étant la longitude et la latitude locales d'un message pair,x1ety1celles d'un message impair — sachant que les positions les plus récentes sont celles d'indexmostRecent(0 ou 1) ; retournenullsi la latitude de la position décodée n'est pas valide (c.-à-d. comprise entre ±90°) ou si la position ne peut pas être déterminée en raison d'un changement de bande de latitude, ou lèveIllegalArgumentExceptionsimostRecentne vaut pas 0 ou 1.
Prenez garde au fait que les positions locales données à decodePosition sont normalisées, donc comprises entre 0 et 1.
3.1.1. Conseils de programmation
Pour calculer le cosinus inverse, noté arccos dans les formules de la §2.2.3, utilisez la méthode acos de Math. Notez que lorsqu'on lui fournit une valeur supérieure à 1 en valeur absolue, elle retourne une valeur spéciale nommée NaN — pour not a number — signalant le fait que le résultat n'est pas défini. Vous pouvez détecter une telle valeur au moyen de la méthode isNaN de Double, et savoir ainsi quand le nombre de zones de longitude doit valoir 1 par définition.
Pour arrondir par défaut, utilisez la méthode floor de Math, et pour arrondir à l'entier le plus proche, la méthode rint.
3.2. Enregistrement AircraftIdentificationMessage
L'enregistrement AircraftIdentificationMessage du sous-paquetage adsb, public, représente un message ADS-B d'identification et de catégorie, du type décrit à la §2.1. Comme toutes les classes représentant des messages ADS-B, il implémente l'interface Message. Il possède les attributs suivants :
long timeStampNs, l'horodatage du message, en nanosecondes,IcaoAddres icaoAddress, l'adresse OACI de l'expéditeur du message,int category, la catégorie d'aéronef de l'expéditeur,CallSign callSign, l'indicatif de l'expéditeur.
Le constructeur compact de AircraftIdentificationMessage lève NullPointerException si icaoAddress ou callSign sont nuls, et IllegalArgumentException si timeStampNs est strictement inférieure à 0.
AircraftIdentificationMessage n'offre qu'une seule méthode publique, et statique, en dehors des méthodes ajoutées automatiquement aux enregistrements Java. Il s'agit de :
AircraftIdentificationMessage of(RawMessage rawMessage), qui retourne le message d'identification correspondant au message brut donné, ounullsi au moins un des caractères de l'indicatif qu'il contient est invalide (voir §2.1).
3.3. Enregistrement AirbornePositionMessage
L'enregistrement AirbornePositionMessage du sous-paquetage adsb, public, représente un message ADS-B de positionnement en vol du type décrit à la section §2.2. Il implémente l'interface Message et possède les attributs suivants :
long timeStampNs, l'horodatage du message, en nanosecondes,IcaoAddres icaoAddress, l'adresse OACI de l'expéditeur du message,double altitude, l'altitude à laquelle se trouvait l'aéronef au moment de l'envoi du message, en mètres,int parity, la parité du message (0 s'il est pair, 1 s'il est impair),double x, la longitude locale et normalisée — donc comprise entre 0 et 1 — à laquelle se trouvait l'aéronef au moment de l'envoi du message,double y, la latitude locale et normalisée à laquelle se trouvait l'aéronef au moment de l'envoi du message.
Le constructeur compact de AirbornePositionMessage lève NullPointerException si icaoAddress est nul, ou IllegalArgumentException si timeStamp est strictement inférieure à 0, ou parity est différent de 0 ou 1, ou x ou y ne sont pas compris entre 0 (inclus) et 1 (exclu).
AirbornePositionMessage n'offre qu'une seule méthode publique, et statique, en dehors des méthodes ajoutées automatiquement aux enregistrements Java. Il s'agit de :
AirbornePositionMessage of(RawMessage rawMessage), qui retourne le message de positionnement en vol correspondant au message brut donné, ounullsi l'altitude qu'il contient est invalide (voir §2.2.5.2).
3.4. Tests
Comme d'habitude, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures à importer dans votre projet.
Pour vous aider à tester votre code, nous vous fournissons néanmoins les 5 premiers messages d'identification figurant parmi les 384 obtenus du fichier d'échantillons fourni à l'étape précédente :
AircraftIdentificationMessage[ timeStampNs=1499146900, icaoAddress=IcaoAddress[string=4D2228], category=163, callSign=CallSign[string=RYR7JD]] AircraftIdentificationMessage[ timeStampNs=2240535600, icaoAddress=IcaoAddress[string=01024C], category=163, callSign=CallSign[string=MSC3361]] AircraftIdentificationMessage[ timeStampNs=2698727800, icaoAddress=IcaoAddress[string=495299], category=163, callSign=CallSign[string=TAP931]] AircraftIdentificationMessage[ timeStampNs=3215880100, icaoAddress=IcaoAddress[string=A4F239], category=165, callSign=CallSign[string=DAL153]] AircraftIdentificationMessage[ timeStampNs=4103219900, icaoAddress=IcaoAddress[string=4B2964], category=161, callSign=CallSign[string=HBPRO]]
ainsi que les 5 premiers messages de positionnement en vol :
AirbornePositionMessage[ timeStampNs=75898000, icaoAddress=IcaoAddress[string=495299], altitude=10546.08, parity=0, x=0.6867904663085938, y=0.7254638671875] AirbornePositionMessage[ timeStampNs=116538700, icaoAddress=IcaoAddress[string=4241A9], altitude=1303.02, parity=0, x=0.702667236328125, y=0.7131423950195312] AirbornePositionMessage[ timeStampNs=138560100, icaoAddress=IcaoAddress[string=4D2228], altitude=10972.800000000001, parity=1, x=0.6243515014648438, y=0.4921417236328125] AirbornePositionMessage[ timeStampNs=208135700, icaoAddress=IcaoAddress[string=4D029F], altitude=4244.34, parity=0, x=0.747222900390625, y=0.7342300415039062] AirbornePositionMessage[ timeStampNs=233069800, icaoAddress=IcaoAddress[string=3C6481], altitude=10370.82, parity=0, x=0.8674850463867188, y=0.7413406372070312]
Finalement, comme aucun des 384 messages obtenus à partir des échantillons ne transmet l'altitude de l'aéronef avec le bit Q valant 0 (voir 2.2.5.2), en voici deux :
8D39203559B225F07550ADBE328F(altitude : environ 3474.72 m),8DAE02C85864A5F5DD4975A1A3F5(altitude : environ 7315.20 m).
4. Résumé
Pour cette étape, vous devez :
- écrire les classes et enregistrements
CprDecoder,AircraftIdentificationMessageetAirbornePositionMessageselon les indications données ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 24 mars 2023 à 18h00, au moyen du programme
Submit.javafourni et des jetons disponibles sur votre page privée.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !