Traitement du signal radio

Javions – étape 3

1. Introduction

Le but de cette étape est d'écrire les classes permettant de traiter le signal provenant de la radio logicielle afin de faciliter le décodage des messages ADS-B, qui sera fait lors de l'étape suivante.

2. Concepts

Pour bien comprendre comment les messages ADS-B sont transmis par les ondes radio, il peut être utile d'examiner comment des messages peuvent être échangés au moyen de signaux lumineux. Les principes sont en effet similaires, mais la compréhension intuitive des signaux lumineux est probablement plus simple.

2.1. Communication par signaux lumineux

Imaginons la situation suivante : deux personnes se trouvent chacune au sommet d'une colline différente, d'où elles peuvent se voir mais pas se parler. Elles désirent néanmoins communiquer, et étant chacune équipée d'une puissante lampe torche, elles décident de les utiliser pour s'échanger des messages.

Pour ce faire, lorsqu'une de ces personnes désire envoyer un message à l'autre, elle commence par représenter ce message sous forme binaire — d'une manière qui importe peu — puis transmet successivement les bits du message en utilisant la convention suivante :

pour transmettre un 0, elle garde sa lampe éteinte durant 5 secondes, puis l'allume durant 5 secondes,
pour transmettre un 1, elle allume sa lampe durant 5 secondes, puis l'éteint durant 5 secondes.

Même si elle est terriblement lente, cette technique de communication fonctionne et a l'avantage d'être simple.

Imaginons maintenant qu'en plus des deux personnes initiales, deux autres personnes désirent également communiquer entre elles depuis les mêmes collines. Si elles utilisent exactement la même technique que les premières, un problème d'interférence se posera, puisqu'il ne sera plus possible de distinguer les signaux lumineux échangés entre les membres du premier groupe de ceux échangés entre les membres du second.

Ce problème a toutefois une solution simple : les membres de chacun des groupes peuvent placer un filtre coloré d'une couleur différente sur leur lampe torche, afin de pouvoir distinguer leurs signaux de ceux de l'autre groupe. Par exemple, le premier groupe pourrait communiquer au moyen de signaux lumineux rouges, le second au moyen de signaux lumineux verts. Et bien entendu, de nombreux autres groupes de personnes pourraient simultanément échanger des messages entre ces deux mêmes collines, pour peu que chaque groupe utilise une couleur qui lui est propre.

2.2. Communication par radio

La transmission de messages radio fonctionne selon un principe similaire à celui décrit ci-dessus, la différence principale étant que le support utilisé est les ondes radio plutôt que les ondes lumineuses.

Au même titre que, dans notre exemple, les différents groupes de personne désirant communiquer simultanément utilisaient des signaux de couleur différente pour éviter les interférences, les différents utilisateurs des ondes radio utilisent des fréquences différentes. Par exemple, les messages ADS-B sont transmis sur la fréquence de 1090 MHz qui leur est réservée, et cela évite qu'ils n'interfèrent, entre autres, avec les signaux envoyés par les détecteurs de victimes d'avalanche sur la fréquence de 457 kHz.

De la même manière que, dans notre exemple, l'émetteur communiquait la valeur des bits du message en allumant ou éteignant sa lampe à différents moments, un émetteur radio peut la communiquer en émettant ou non un signal à la fréquence qui lui est réservée.

Ainsi, les bits des messages ADS-B sont transmis de la même manière que dans notre exemple, si ce n'est que le temps nécessaire à la transmission d'un bit est de 1 μs (une microseconde) plutôt que de 10 secondes. En d'autres termes, pour émettre un bit d'un messages ADS-B, un émetteur doit :

si le bit vaut 0 : ne rien émettre durant ½ μs, puis émettre une onde sinusoïdale d'une fréquence de 1090 MHz durant ½ μs,
si le bit vaut 1 : émettre une onde sinusoïdale d'une fréquence de 1090 MHz durant ½ μs, puis ne rien émettre durant ½ μs.

L'onde sinusoïdale — dont la fréquence est de 1090 MHz dans le cas de ADS-B — est appelée onde porteuse ou simplement porteuse (carrier wave ou simplement carrier en anglais) puisqu'elle sert à transporter l'information. Dans l'exemple de la section précédente, c'est la lumière d'une couleur donnée qui servait de porteuse aux messages du groupe auquel cette couleur était attribuée.

Bien entendu, pour que la porteuse puisse effectivement transporter de l'information, il faut que l'une ou l'autre de ses caractéristiques change au cours du temps, en fonction de l'information à transmettre. Dans le cas des messages ADS-B, la caractéristique qui change est que la porteuse est transmise ou non à un instant donné. De manière similaire, dans la section précédente, la lampe d'un émetteur était allumée ou non à un instant donné, en fonction du message à transmettre.

Le fait de modifier ainsi, au cours du temps, une caractéristique de la porteuse afin de lui faire transmettre de l'information s'appelle modulation, et on dit que la porteuse est modulée par le signal à transmettre. La technique de modulation utilisée pour les messages ADS-B et qui consiste, une fois encore, à émettre ou non cette porteuse durant certaines périodes, se nomme modulation d'impulsions en position (pulse-position modulation, abrégé PPM). Le terme impulsion (pulse) désigne ici les périodes durant laquelle la porteuse est transmises.

La modulation PPM est une technique particulièrement simple, mais il en existe de nombreuses autres qui ne seront pas décrites ici car elles ne sont pas utiles au projet¹.

2.3. Radio logicielle

Pour recevoir les messages ADS-B, nous utiliserons une radio logicielle (software-defined radio, abrégé SDR) — une AirSpy R2 — et il convient donc de comprendre comment de telles radios fonctionnent, au moins dans les grandes lignes.

Une radio logicielle a la capacité de recevoir les ondes radio dans une plage (ou bande) de fréquence dont la largeur est fixe et dépend de la radio. Dans le cas de la AirSpy, cette plage a une largeur de 10 MHz.

La position de cette plage est choisie par l'utilisateur de la radio, qui la règle (tune) sur la fréquence centrale (center frequency) de son choix. Ainsi, pour recevoir les messages ADS-B, une AirSpy doit être réglée sur la fréquence centrale de 1090 MHz, et elle est alors capable de recevoir toutes les ondes dont la fréquence est comprise entre 1085 et 1095 MHz.

Pour reprendre l'analogie de la §2.1, une radio logicielle se comporte donc un peu comme une paire de lunettes réglables qui, lorsqu'on les règle sur une couleur donnée, ne laissent passer que la lumière de cette couleur-là et des couleurs proches, bloquant toutes les autres couleurs.

Une fois réglée sur une fréquence centrale, par exemple 1090 MHz, une radio logicielle effectue ensuite un décalage de fréquence (downconversion) du signal reçu. Dans le cas de la AirSpy, ce décalage est fait de manière à ce que la fréquence centrale soit décalée à 5 MHz, et donc que la plage captée aille désormais de 0 à 10 MHz. Pour les messages ADS-B cela signifie que la porteuse est maintenant une onde sinusoïdale d'une fréquence de 5 MHz, ce qui change bien entendu son aspect mais ne rend pas le décodage des messages plus difficile, puisque seule l'absence ou la présence de la porteuse importe, et pas sa fréquence exacte.

Dans notre analogie, ce décalage de fréquence correspondrait à un changement de couleur. Par exemple, le rouge serait transformé en vert, l'orange en turquoise, etc. Là aussi, le fait que la couleur change ne rend pas le décodage des messages plus difficile, car seul le fait que la lampe soit allumée ou éteinte compte, pas sa couleur exacte.

Finalement, une fois que la plage de 10 MHz entourant la fréquence centrale a été ainsi décalée, le signal est échantillonné (sampled) en vue d'être transmis à l'ordinateur. C'est-à-dire que sa valeur est mesurée périodiquement, et ces mesures — que l'on nomme des échantillons (samples) — sont ensuite transmises à l'ordinateur.

La radio AirSpy effectue cet échantillonnage à la fréquence d'échantillonnage (sampling frequency) de 20 MHz, ce qui signifie que le temps séparant deux échantillons — la période d'échantillonnage (sampling period) — est de 50 nanosecondes.

La fréquence d'échantillonnage a été choisie par les concepteurs de la AirSpy afin de satisfaire la condition du théorème d'échantillonnage (sampling theorem). Celui-ci nous apprend que, pour échantillonner correctement un signal, la fréquence d'échantillonnage doit être au moins égale au double de la plus haute fréquence du signal — qui est ici de 10 MHz.

On comprend maintenant que la raison pour laquelle le signal est décalé en fréquence par une radio logicielle avant d'être échantillonné est que cela permet de réduire considérablement la fréquence d'échantillonnage, et donc la quantité de données à transmettre à l'ordinateur, de même que la complexité et le coût de l'électronique.

En effet, si une radio logicielle échantillonnait directement le signal contenant les messages ADS-B à 1090 MHz, alors elle devrait le faire à une fréquence d'échantillonnage de 2180 MHz au minimum, et donc transmettre plus de 2 milliards d'échantillons par seconde à l'ordinateur. En décalant le signal avant de le numériser, elle peut se permettre de l'échantillonner à 20 MHz « seulement », et donc de ne transmettre « que » 20 millions d'échantillons par seconde à l'ordinateur — un gain d'un facteur 100 environ.

2.4. Traitement des échantillons

Une fois reçus de la radio logicielle, les échantillons du signal doivent être traités par notre programme en vue de faciliter le décodage des messages ADS-B. Ce traitement est décrit dans les sections suivantes, et consiste en trois phases :

la séquence d'octets reçue de la radio est organisée en une séquence d'échantillons signés de 12 bits chacun,
le signal est décalé en fréquence une seconde fois afin d'amener la fréquence centrale à 0 Hz,
le signal est filtré par une moyenne mobile, et sa puissance est calculée.

Le décodage des messages ADS-B sera fait à l'étape 4, en se basant uniquement sur la puissance du signal produite à la fin de la dernière phase ci-dessus.

2.4.1. Transformation des octets

Le convertisseur analogique/digital (AD) de la AirSpy a une précision de 12 bits. Cela signifie que chaque échantillon qu'elle produit peut prendre une valeur parmi 4096 (2¹²).

La AirSpy transmet ces échantillons de 12 bits à l'ordinateur auquel elle est connectée sous la forme d'une séquence d'octets, en utilisant 2 octets par échantillon. Cette organisation n'est pas optimale, puisque chaque échantillon de 12 bits est transmis au moyen de 16 bits et 4 bits sont donc gaspillés, mais a l'avantage d'être simple.

L'ordre dans lequel les deux octets d'un échantillon sont transmis peut toutefois surprendre, puisque le premier d'entre eux contient toujours les 8 bits de poids faible (!) de l'échantillon, tandis que le second contient 4 bits nuls ainsi que les 4 bits de poids fort de l'échantillon. Par exemple, la séquence composée des deux octets FD₁₆ 07₁₆ représente un échantillon de 12 bits dont les 4 bits de poids fort valent 7₁₆ et les 8 bits de poids faible FD₁₆, donc 7FD₁₆ (soit 2045₁₀).

L'ordre utilisé pour la transmission des octets ne correspond donc pas à la manière dont nous écrivons habituellement les nombres, c.-à-d. en mettant les chiffres de poids fort en premier. Toutefois, la convention consistant à mettre les octets de poids faible en premier, communément appelée little-endian, a un certain nombre d'avantages et se rencontre donc fréquemment en informatique.

Une fois les deux octets représentant un échantillon correctement combinés en une seule valeur de 12 bits, cette dernière est recentrée autour de 0 par soustraction d'un « biais » valant 2048 (2¹¹). Cela implique que, pour la suite du traitement, les échantillons sont des valeurs de 12 bits signées, comprises entre -2048 (inclus) et +2047 (inclus).

Par exemple, après soustraction du biais, l'échantillon 7FD₁₆ mentionné ci-dessus est donc interprété comme ayant la valeur -3.

2.4.2. Décalage de fréquence

Une fois les octets provenant de la radio transformés en échantillons signés, le traitement numérique du signal peut commencer. Le but de ce traitement est d'isoler de manière aussi propre que possible le signal qui nous intéresse, qui se trouve à ce stade à la fréquence centrale de 5 MHz.

Pour ce faire, on commence par effectuer un décalage de fréquence de -5 MHz, afin de placer la fréquence centrale à 0 Hz. Le but de cette opération est de simplifier le filtrage ultérieur du signal.

Il se trouve que pour décaler un signal échantillonné d'une fréquence donnée, il suffit de multiplier ses échantillons par une exponentielle complexe, de la manière suivante :

\[ x^{\prime}_n = x_n\exp\left(2\pi\,f_c\,t_s\,n\,\mathrm{i}\right) \]

où $x_n$ représente l'échantillon d'index $n$ du signal original, $x_n^\prime$ l'échantillon correspondant du signal décalé en fréquence, $f_c$ le décalage en fréquence désiré, $t_s$ la période d'échantillonnage et $\mathrm{i}$ l'unité complexe.

Dans notre cas, il faut noter que le décalage en fréquence $f_c$ que nous désirons effectuer, de -5 MHz, est lié par une relation simple à la fréquence d'échantillonnage $f_s$ de la AirSpy, qui est de 20 MHz, puisqu'on a :

\[ f_c = -\frac{1}{4} f_s \]

Étant donné que la période d'échantillonnage $t_s$ est simplement l'inverse de la fréquence d'échantillonnage, on a :

\[ f_c = -\frac{1}{4} f_s = -\frac{1}{4}\cdot\frac{1}{t_s} = -\frac{1}{4\,t_s} \]

La formule de décalage donnée plus haut se simplifie donc ainsi :

\begin{align} x^{\prime}_n &= x_n\exp\left(2\pi\,(-\frac{1}{4\,t_s})\,t_s\,n\,\mathrm{i}\right)\\ &= x_n\exp\left(-\frac{\pi}{2}\,n\,\mathrm{i}\right) \end{align}

Sachant que $\exp(\theta\,\mathrm{i}) = \cos\theta + \mathrm{i}\,\sin\theta$, on peut récrire cette équation ainsi :

\[ x^\prime_n = x_n\left[\cos\left(-\frac{\pi}{2}\,n\right) + \mathrm{i}\,\sin\left(-\frac{\pi}{2}\,n\right)\right] \]

Comme $n = 0, 1, 2, \ldots$, les angles passés aux fonctions sinus et cosinus dans cette formule correspondent tous à des quarts de tour, et ces fonctions produisent donc toujours -1, 0 ou +1. On le constate en évaluant cette formule pour les six premiers échantillons :

\begin{align} x^\prime_0 &= x_0\cdot 1\\ x^\prime_1 &= x_1\cdot(-\mathrm{i})\\ x^\prime_2 &= x_2\cdot(-1)\\ x^\prime_3 &= x_3\cdot \mathrm{i}\\ x^\prime_4 &= x_4\cdot 1\\ x^\prime_5 &= x_5\cdot(-\mathrm{i})\\ \end{align}

En d'autres termes, le décalage en fréquence désiré peut s'effectuer simplement en multipliant la séquence des échantillons originaux par la séquence $1, -\mathrm{i}, -1, \mathrm{i}, \ldots$

Comme on le constate, après le décalage en fréquence, le signal devient complexe. C'est-à-dire que les échantillons ne sont plus simplement des nombres réels, mais bien des nombres complexes. Pour être précis, après décalage, les échantillons d'index pair sont purement réels, tandis que les échantillons d'index impair sont purement imaginaires.

2.4.3. Représentation IQ

Pour représenter les échantillons après décalage, une solution serait bien entendu d'utiliser des nombres complexes. Toutefois, dans le monde de la radio, une autre technique est généralement utilisée, et consiste à séparer la séquence des échantillons en deux sous-séquences, la première contenant la partie réelle des échantillons, la seconde leur partie imaginaire.

Dans cette représentation, la sous-séquence contenant la partie réelle des échantillons est appelée « en phase » (in-phase, abrégé I), tandis que celle contenant la partie imaginaire est appelée « quadrature » (quadrature, abrégé Q). Les abréviations utilisées sont malheureuses, car la lettre I évoque la partie imaginaire, alors que la sous-séquence I contient en réalité la partie réelle des échantillons.

Exprimés dans cette représentation dite « I/Q », les six échantillons donnés plus haut sont :

\begin{align} I &= x_0, 0, -x_2, 0, x_4, 0, \ldots\\ Q &= 0, -x_1, 0, x_3, 0, -x_5, \ldots \end{align}

Comme on le voit, la séquence $I$ ne contient que les échantillons pairs, avec leur signe inversé une fois sur deux, entre lesquels des 0 sont placés. La séquence $Q$ est similaire, mais contient les échantillons impairs.

2.4.4. Filtrage « passe-bas »

Comme nous l'avons dit, le but du décalage en fréquence est de placer la fréquence centrale à 0 Hz afin de faciliter le filtrage du signal. Ce filtrage permet de ne garder que les basses fréquences, donc proches de 0, en éliminant autant que possible les fréquences plus élevées.

Le filtrage numérique du signal peut se faire avec des techniques plus ou moins sophistiquées en fonction des besoins, mais dans ce projet nous utiliserons une technique extrêmement simple, la moyenne mobile (moving average), aussi appelée moyenne glissante.

L'idée de la moyenne mobile est de filtrer une séquence d'échantillons en en produisant une nouvelle dont chaque échantillon n'est rien d'autre que la moyenne d'un certain nombre d'échantillons consécutifs de la séquence originale. Cela permet de réduire les fluctuations rapides (les hautes fréquences), tout en conservant les fluctuations lentes (les basses fréquences).

Par exemple, si $x_n$ est une séquence d'échantillons, on peut la filtrer par une moyenne glissante de taille 3 pour produire une nouvelle séquence $x_n^\prime$ définie ainsi :

\[ x_n^\prime = \frac{1}{3}\left(x_{n-2} + x_{n-1} + x_n\right) \]

Afin que cette formule soit bien définie pour toutes les valeurs de $n$, y compris 0 et 1, on peut étendre la séquence originale en définissant $x_n = 0$ pour $n < 0$.

Pour filtrer les échantillons provenant de la AirSpy, nous utiliserons un filtre de taille 8, c.-à-d. une moyenne glissante combinant 8 échantillons successifs. Pour simplifier les calculs, nous omettrons de plus la division par 8, nous contentant donc d'additionner 8 échantillons successifs. Le signal résultant sera donc amplifié d'un facteur 8 par rapport à celui que nous aurions obtenu en faisant une réelle moyenne, mais cela n'aura aucun impact sur le décodage des messages, qui ne se base que sur la forme du signal et pas sur sa valeur exacte.

Ainsi, la version filtrée de la séquence $I$, que nous noterons $I^\prime$, est définie ainsi : \[ I^\prime_n = I_{n-7} + I_{n-6} + I_{n-5} + I_{n-4} + I_{n-3} + I_{n-2} + I_{n-1} + I_n \]

Sachant que les éléments de $I$ d'index impair sont nuls, on peut récrire cette formule en distinguant deux cas :

\[ I^\prime_n = \begin{cases} I_{n-6} + I_{n-4} + I_{n-2} + I_n & \text{si $n$ est pair}\\ I_{n-7} + I_{n-5} + I_{n-3} + I_{n-1} & \text{si $n$ est impair}\\ \end{cases} \]

On en déduit que chaque élément de $I^\prime$ d'index impair est égal à celui d'index pair qui le précède : $I^\prime_{2n+1} = I^\prime_{2n}$

De manière similaire, pour $Q^\prime$, on a :

\begin{align} Q^\prime_n &= Q_{n-7} + Q_{n-6} + Q_{n-5} + Q_{n-4} + Q_{n-3} + Q_{n-2} + Q_{n-1} + Q_n \end{align}

donc, comme les éléments de $Q$ d'index pair sont nuls :

\[ Q^\prime_n = \begin{cases} Q_{n-7} + Q_{n-5} + Q_{n-3} + Q_{n-1} & \text{si $n$ est pair}\\ Q_{n-6} + Q_{n-4} + Q_{n-2} + Q_n & \text{si $n$ est impair}\\ \end{cases} \]

On en déduit que chaque élément de $Q^\prime$ d'index impair est égal à celui d'index pair qui le suit : $Q^\prime_{2n+1} = Q^\prime_{2n+2}$

En combinant ces observations concernant les répétitions dans les éléments de $I^\prime$ et $Q^\prime$, on en conclut que ces séquences peuvent s'écrire ainsi :

\begin{align} I^\prime &= I^\prime_0, I^\prime_1, I^\prime_2, I^\prime_3, I^\prime_4, \ldots = I^\prime_0, I^\prime_0, I^\prime_2, I^\prime_2, I^\prime_4, \ldots\\ Q^\prime &= Q^\prime_0, Q^\prime_1, Q^\prime_2, Q^\prime_3, Q^\prime_4, \ldots = Q^\prime_0, Q^\prime_2, Q^\prime_2, Q^\prime_4, Q^\prime_4, \ldots \end{align}

2.4.5. Décimation

Comme chacune des deux séquences $I^{\prime}$ et $Q^{\prime}$ est constituée de valeurs qui ne changent qu'une fois sur deux, nous les « décimerons » en n'en conservant que les éléments impairs. Nous noterons $I^{\prime\prime}$ et $Q^{\prime\prime}$ les séquences ainsi décimées :

\begin{align} I^{\prime\prime} &= I^\prime_0, I^\prime_2, I^\prime_4, \ldots\\ Q^{\prime\prime} &= Q^\prime_2, Q^\prime_4, Q^\prime_6, \ldots\\ \end{align}

Cette décimation simplifie le code et n'a pas d'impact négatif sur le décodage des messages ADS-B, pour peu bien entendu qu'on tienne compte du fait qu'en supprimant ainsi un échantillon sur deux, on double la période d'échantillonnage $t_s$. Cela signifie que, après décimation, les échantillons sont espacés de 100 ns plutôt que de 50 ns.

Le terme d'index $n$ de $I^{\prime\prime}$ étant celui d'index $2n$ de $I^\prime$, on a :

\begin{align} I^{\prime\prime}_n &= I^\prime_{2n}\\ &= I_{2n-6} + I_{2n-4} + I_{2n-2} + I_{2n}\\ &= ±(x_{2n-6} - x_{2n-4} + x_{2n-2} - x_{2n}) \end{align}

où le $±$ de la dernière ligne exprime le fait que le signe placé devant l'expression parenthésée est alternativement positif et négatif mais, comme nous le verrons plus bas, il ne joue finalement aucun rôle dans le calcul qui nous intéresse.

De même, le terme d'index $n$ de $Q^{\prime\prime}$ vaut :

\begin{align} Q^{\prime\prime}_n &= Q^\prime_{2n+2}\\ &= Q_{2n-5} + Q_{2n-3} + Q_{2n-1} + Q_{2n+1}\\ &= ±(x_{2n-5} - x_{2n-3} + x_{2n-1} - x_{2n+1}) \end{align}

2.4.6. Calcul de la puissance

La dernière étape du traitement du signal consiste à déterminer sa puissance à chaque instant. C'est grâce à elle qu'il sera possible de déterminer si, à un instant donné, la porteuse est présente ou non.

La puissance (power) d'un signal à un instant donné est simplement la valeur absolue de ce signal — ou son module s'il est complexe —, élevée au carré. Dans notre cas, cette puissance, notée $P$, se détermine donc ainsi :

\[ P_n = \left(I^{\prime\prime}_n\right)^2 + \left(Q^{\prime\prime}_n\right)^2 \]

En substituant $I^{\prime\prime}_n$ et $Q^{\prime\prime}_n$ par leur définition, on obtient finalement :

\[ P_n = (x_{2n-6} - x_{2n-4} + x_{2n-2} - x_{2n})^2 + (x_{2n-5} - x_{2n-3} + x_{2n-1} - x_{2n+1})^2 \]

On notera en particulier qu'en raison de l'élévation au carré, les changements de signes exprimés plus haut par des $±$ ont disparu.

2.4.7. Résumé et mise en œuvre

Les sections ci-dessus peuvent donner l'impression que le filtrage à appliquer au signal est compliqué. Or même s'il est vrai que la quantité de concepts à comprendre pour savoir pourquoi la formule déterminant la puissance a la forme qu'elle a, écrire le code correspondant peut se faire sans saisir tous les détails.

En effet, cette formule ne dépend que de 8 échantillons obtenus consécutivement depuis la radio, notés $x_{2n-6}$ à $x_{2n+1}$, qu'elle combine de manière fort simple. En résumé, la production d'un nouvel échantillon de puissance se fait en :

obtenant 2 nouveaux échantillons de la radio,
les combinant avec les 6 précédents au moyen de la formule plus haut.

Pour mettre cela en œuvre, on peut utiliser un tableau, initialisé à 0, pour stocker les huit derniers échantillons obtenus de la radio. Ensuite, chaque fois que l'on désire obtenir un nouvel échantillon de puissance, on obtient deux échantillons de la radio, que l'on stocke dans le tableau à la place des deux les plus anciens, avant d'utiliser la totalité de ses valeurs pour calculer la formule donnée à la section précédente.

2.5. Traitement par lots

La séquence des échantillons produite par la radio est conceptuellement infinie, puisque tant et aussi longtemps que la radio fonctionne, elle fournit en permanence de nouveaux échantillons. Jusqu'à présent, nous avons fait l'hypothèse que ces échantillons étaient simplement traités au fur et à mesure de leur arrivée, l'un après l'autre.

Toutefois, pour des questions de performance, nous traiterons en réalité les échantillons par lots (batches). Par exemple, plutôt que de lire l'un après l'autre les octets produits par la radio, un lot de quelques milliers d'échantillons sera lu en une fois et placé dans un tableau. Ensuite, les octets de ce tableau seront extraits deux par deux et placés dans un autre tableau, contenant les échantillons de 12 bits signés. Le calcul de la puissance sera fait sur les échantillons de ce tableau, et les échantillons de puissance résultants seront placés dans un autre tableau encore.

Toujours pour des questions de performance, ces tableaux seront généralement réutilisés. Ainsi, il n'existera qu'un seul tableau destiné à contenir les octets provenant de la radio. Au début de l'exécution du programme, il sera rempli avec les premiers octets reçus, puis ces octets seront transformés en échantillons signés, et le tableau réutilisé pour contenir les octets suivants.

Ce principe sera également appliqué au tableau contenant les échantillons signés, qui n'existera aussi qu'à un exemplaire. Par contre, il existera deux tableaux contenant les échantillons de puissance, pour la raison expliquée à la section suivante.

2.6. Fenêtrage

Par rapport à un traitement séquentiel simple, le traitement par lots permet d'obtenir de meilleures performances mais ne facilite pas le décodage des messages ADS-B. En effet, comme nous le verrons à l'étape suivante, un tel message s'étend sur un total de 1200 échantillons de puissance, et il est donc possible que les échantillons d'un seul message appartiennent à deux lots différents — voire à plus de deux si les lots font moins de 1200 échantillons, mais nous nous arrangerons pour que ce ne soit pas le cas.

Pour le décodage des messages, l'idéal est donc d'avoir à tout instant accès à la totalité des échantillons de puissance situés dans une fenêtre (window) de 1200 échantillons consécutifs. Dans ce cas, le décodage des messages ADS-B consiste simplement à faire avancer cette fenêtre sur les échantillons, jusqu'à reconnaître le début d'un message. À ce moment-là, le message peut facilement être décodé puisque tous ses échantillons sont disponibles dans la fenêtre. Une fois le décodage terminé, la recherche du prochain message peut se poursuivre en faisant avancer la fenêtre de 1200 échantillons. Et ainsi de suite.

3. Mise en œuvre Java

Toutes les classes de cette étape appartiennent au sous-paquetage demodulation du paquetage principal ch.epfl.javions, qui contient tout le code lié à la démodulation des messages ADS-B.

3.1. Classe `SamplesDecoder`

La classe SamplesDecoder du sous-paquetage demodulation, publique et finale, représente un « décodeur d'échantillons », c.-à-d. un objet capable de transformer les octets provenant de la AirSpy en des échantillons de 12 bits signés.

Pour des raisons d'efficacité, ce décodeur fonctionne par lots, comme expliqué plus haut. La taille des lots, c.-à-d. le nombre d'échantillons à produire lors de chaque conversion, est passée en argument au constructeur de la classe, qui est :

SamplesDecoder(InputStream stream, int batchSize), qui retourne un décodeur d'échantillons utilisant le flot d'entrée donné pour obtenir les octets de la radio AirSpy et produisant les échantillons par lots de taille donnée ; lève IllegalArgumentException si la taille des lots n'est pas strictement positive, ou NullPointerException si le flot est nul.

Le flot passé au constructeur est supposé contenir des octets représentant des échantillons au format utilisé par la AirSpy et décrit à la §2.4.1. Notez bien qu'aucun octet ne doit être lu depuis ce flot par le constructeur, cette tâche étant réservée à la seule méthode publique de SamplesDecoder :

int readBatch(short[] batch) throws IOException, qui lit depuis le flot passé au constructeur le nombre d'octets correspondant à un lot, puis convertit comme décrit à la 2.4.1 ces octets en échantillons signés, qui sont placés dans le tableau passé en argument ; le nombre d'échantillons effectivement converti est retourné, et il est toujours égal à la taille du lot sauf lorsque la fin du flot a été atteinte avant d'avoir pu lire assez d'octets, auquel cas il est égal au nombre d'octets lus divisé par deux, arrondi vers le bas ; lève IOException en cas d'erreur d'entrée/sortie, ou IllegalArgumentException si la taille du tableau passé en argument n'est pas égale à la taille d'un lot.

3.1.1. Conseils de programmation

La raison pour laquelle la taille des lots est passée au constructeur est que cela lui permet de créer et stocker dans un attribut privé de la classe l'unique tableau d'octets — de type byte[] — qui sera utilisé pour lire les octets correspondant à un lot d'échantillons. La taille de ce tableau est bien entendu égale au double de la taille des lots, car chaque échantillon est représenté par deux octets.

Le transfert des octets du flot vers ce tableau peut se faire au moyen d'un unique appel à la méthode readNBytes de InputStream.

3.2. Classe `PowerComputer`

La classe PowerComputer du sous-paquetage demodulation, publique et finale, représente un « calculateur de puissance », c.-à-d. un objet capable de calculer les échantillons de puissance du signal à partir des échantillons signés produits par un décodeur d'échantillons.

Tout comme SamplesDecoder, PowerComputer travaille par lots, et la taille des lots est donc passée à son unique constructeur public :

PowerComputer(InputStream stream, int batchSize), qui retourne un calculateur de puissance utilisant le flot d'entrée donné pour obtenir les octets de la radio AirSpy et produisant des échantillons de puissance par lots de taille donnée ; lève IllegalArgumentException si la taille des lots n'est pas un multiple de 8 — le nombre d'échantillons utilisés pour la moyenne mobile — strictement positif.

Tout comme celui de SamplesDecoder, ce constructeur se charge de créer l'unique tableau destiné à contenir les échantillons, qui sera passé à la méthode readBatch de SamplesDecoder. L'instance de SamplesDecoder servant à produire ces échantillons à partir des octets du flot est également créée par le constructeur de PowerComputer, et stockée dans un autre attribut privé de la classe.

En plus de ce constructeur, PowerComputer offre l'unique méthode publique suivante :

int readBatch(int[] batch) throws IOException, qui lit depuis le décodeur d'échantillons le nombre d'échantillons nécessaire au calcul d'un lot d'échantillons de puissance, puis les calcule au moyen de la formule donnée à la §2.4.6 et les place dans le tableau passé en argument ; retourne le nombre d'échantillons de puissance placés dans le tableau, ou lève IOException en cas d'erreur d'entrée/sortie, ou IllegalArgumentException si la taille du tableau passé en argument n'est pas égale à la taille d'un lot.

3.2.1. Conseils de programmation

Pour mémoire, la formule donnée à la §2.4.6 pour le calcul de l'échantillon de puissance d'index $n$ est :

\[ P_n = (x_{2n-6} - x_{2n-4} + x_{2n-2} - x_{2n})^2 + (x_{2n-5} - x_{2n-3} + x_{2n-1} - x_{2n+1})^2 \]

Pour pouvoir la calculer, il faut donc avoir à disposition les huit derniers échantillons produits par la radio et notés $x_{2n-6}$ à $x_{2n+1}$. Ils peuvent naturellement être stockés dans un tableau de taille huit, lui-même placé dans un attribut privé de PowerComputer. Notez bien que ce tableau ne peut pas être recréé à chaque appel à readBatch, car au début d'un lot, une partie des échantillons qu'il contient doit provenir du lot précédent !

Ce tableau doit être géré comme s'il était circulaire, dans le sens où lorsqu'un nouvel échantillon y est placé, il doit remplacer le plus ancien échantillon qui s'y trouve. L'index de cet élément le plus ancien peut être soit stocké dans un attribut de la classe, soit déterminé par calcul.

3.3. Classe `PowerWindow`

La classe PowerWindow du sous-paquetage demodulation, publique et finale, représente une fenêtre de taille fixe sur une séquence d'échantillons de puissance produits par un calculateur de puissance.

PowerWindow offre un unique constructeur public :

PowerWindow(InputStream stream, int windowSize) throws IOException, qui retourne une fenêtre de taille donnée sur la séquence d'échantillons de puissance calculés à partir des octets fournis par le flot d'entrée donné ; lève IllegalArgumentException si la taille de la fenêtre donnée n'est pas comprise entre 0 (exclu) et 2¹⁶ (inclus).

La raison pour laquelle le constructeur limite à 2¹⁶ la taille de la fenêtre est que cette taille est celle des lots d'échantillons obtenus depuis le calculateur de puissance. En s'assurant que la fenêtre n'est pas plus grande qu'un lot, on garantit qu'elle ne peut jamais chevaucher plus de deux lots.

Tout comme ceux des deux classes précédentes, ce constructeur se charge de créer et stocker les deux tableaux destinés à contenir les échantillons de puissance. L'instance de PowerComputer servant à calculer les échantillons de puissance à partir des octets du flot est également créée par le constructeur de PowerWindow et stockée dans un attribut privé.

En plus de ce constructeur, PowerWindow offre les méthodes publiques suivantes :

int size(), qui retourne la taille de la fenêtre,
long position(), qui retourne la position actuelle de la fenêtre par rapport au début du flot de valeurs de puissance, qui vaut initialement 0 et est incrémentée à chaque appel à advance (voir plus bas),
boolean isFull(), qui retourne vrai ssi la fenêtre est pleine, c.-à-d. qu'elle contient autant d'échantillons que sa taille ; cela est toujours vrai, sauf lorsque la fin du flot d'échantillons a été atteinte, et que la fenêtre la dépasse,
int get(int i), qui retourne l'échantillon de puissance à l'index donné de la fenêtre, ou lève IndexOutOfBoundsException si cet index n'est pas compris entre 0 (inclus) et la taille de la fenêtre (exclu),
void advance() throws IOException, qui avance la fenêtre d'un échantillon,
void advanceBy(int offset) throws IOException, qui avance la fenêtre du nombre d'échantillons donné, comme si la méthode advance avait été appelée le nombre de fois donné, ou lève IllegalArgumentException si ce nombre n'est pas positif ou nul.

3.3.1. Conseils de programmation

Étant donné que la fenêtre a une taille qui est inférieure ou égale à celle d'un lot, il est possible qu'elle chevauche deux lots, mais pas plus.

Dès lors, PowerWindow doit toujours gérer deux tableaux contenant chacun un lot, stockés dans des attributs privés de la classe. Le premier de ces tableaux est destiné à contenir les lots d'index pair, l'autre ceux d'index impair.

Lorsqu'une instance de PowerWindow est créée, le premier de ces tableaux est immédiatement rempli avec le premier lot d'échantillons de puissance, obtenu du calculateur. Le second est par contre laissé vide, et il le reste tant et aussi longtemps que la fenêtre est totalement contenue dans le premier lot. Dès qu'elle chevauche le second lot, le contenu de ce lot est obtenu du calculateur et placé dans le second tableau.

Plus tard, lorsque la fenêtre est totalement contenue dans le second lot, alors le contenu du premier tableau n'est plus nécessaire. Le rôle des deux tableaux est alors échangé, de manière à ce que le premier élément de la fenêtre soit toujours dans le premier tableau. Dès que la fenêtre commence à chevaucher le troisième lot, son contenu est chargé dans ce qui est maintenant le second tableau, et ainsi de suite.

3.4. Tests

Comme pour l'étape précédente, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures à importer dans votre projet.

En plus de ce fichier de vérification de signatures, nous vous fournissons un fichier nommé samples.bin qui contient 4804 octets produits par une radio AirSpy, à partir desquels vous devriez pouvoir produire 1201 échantillons de puissance.

Si vous utilisez votre classe SamplesDecoder pour décoder les échantillons contenus dans ce fichier, les 10 premières valeurs obtenues devraient être :

-3 8 -9 -8 -5 -8 -12 -16 -23 -9

Et si vous utilisez votre classe PowerComputer pour calculer les échantillons de puissance correspondant à ces valeurs, les 10 premiers d'entre eux devraient être :

73 292 65 745 98 4226 12244 25722 36818 23825

On vérifie aisément que ces échantillons de puissance sont bien ceux attendus étant donnés les échantillons de départ et la formule de la §2.4.6 :

\begin{align} 73 &= (-(-3))^2 + (-8)^2\\ 292 &= (-3 - (-9))^2 + (8 - (-8))^2\\ 65 &= (-(-3) + (-9) - (-5))^2 + (-8 + (-8) - (-8))^2\\ \ldots \end{align}

Pour vérifier visuellement les valeurs obtenues, vous pouvez imprimer à l'écran les 160 premiers échantillons de puissance puis les copier/coller dans un tableur afin d'obtenir un graphe. Vous devriez obtenir quelque chose de similaire à l'image ci-dessous, sur laquelle les pics de puissance correspondants aux périodes durant laquelle la porteuse était transmise sont bien visibles.

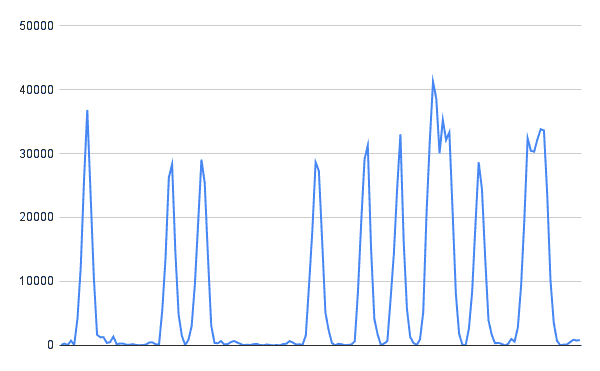
adsb-msg-power-graph;8.png — Figure 1 : Les 160 premières puissances correspondant à `samples.bin`

Comme nous le verrons à l'étape suivante, les 160 échantillons ci-dessus représentent le début d'un message ADS-B : les 80 premiers contiennent ce que l'on nomme le préambule du message, les 80 suivants contiennent les 8 bits du premier octet.

4. Résumé

Pour cette étape, vous devez :

écrire les classes SamplesDecoder, PowerComputer et PowerWindow selon les indications données ci-dessus,
tester votre code,
documenter la totalité des entités publiques que vous avez définies,
rendre votre code au plus tard le 10 mars 2023 à 18h00, au moyen du programme Submit.java fourni et des jetons disponibles sur votre page privée.

Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.

N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !

Notes de bas de page

On peut par exemples citer la modulation d'amplitude (amplitude modulation, abrégée AM) ou la modulation de fréquence (frequency modulation, abrégée FM) qui consistent respectivement à moduler l'amplitude et la fréquence de la porteuse en fonction du signal à transmettre. Ces techniques de modulation sont utilisées pour transmettre des signaux analogiques, principalement du son, et ont donné leur nom aux stations de radio commerciales AM ou FM.

De nombreuses autres techniques de modulation, beaucoup plus complexes, sont utilisées pour transmettre les signaux numériques comme ceux utilisés par la téléphonie mobile, les réseaux sans fil (Wi-Fi, Bluetooth, etc.), la radio numérique DAB+, la télévision numérique, etc.