Mise en place
Javions – étape 1
1. Introduction
Cette première étape du projet Javions a pour but de définir un certain nombre de classes relativement simples qui seront utiles par la suite.
Comme toutes les descriptions d'étapes, celle-ci commence par une introduction aux concepts nécessaires à sa réalisation (§2), suivie d'une présentation de leur mise en œuvre en Java (§3).
Si vous travaillez en groupe, vous êtes toutefois priés de lire, avant de continuer, les guides Travailler en groupe et Synchroniser son travail, qui vous aideront à bien vous organiser.
2. Concepts
Comme nous l'avons vu dans l'introduction au projet, l'interface graphique de Javions montre une carte sur laquelle les aéronefs dont on reçoit des messages sont affichés. La question se pose donc de savoir comment obtenir cette carte, et comment représenter la position d'un aéronef, aussi bien dans l'espace que sur la carte.
2.1. OpenStreetMap
La carte sur laquelle nous afficherons les aéronefs provient du projet OpenStreetMap — souvent abrégé OSM —, qui vise à créer une base de données géographique du monde entier, librement utilisable et modifiable. L'idée est donc similaire à celle de Wikipedia, mais pour les données géographiques.
Les données d'OpenStreetMap peuvent être utilisées de différentes manières, entre autres pour dessiner une carte comme celle sur laquelle nous afficherons les aéronefs, visible ci-dessous.
2.2. Coordonnées WGS 84
Pour pouvoir afficher un aéronef sur la carte, il faut savoir où il se trouve dans l'espace, et donc avoir une manière de représenter sa position n'importe où dans le voisinage de la Terre. Nous utiliserons pour cela les coordonnées géographiques, qui représentent la position d'un point au moyen de deux angles qui sont :
- la longitude \(\lambda\), qui est l'angle entre le point et le méridien origine — un méridien étant un demi-cercle reliant les deux pôles,
- la latitude \(\phi\), qui est l'angle entre le point et l'équateur.
Ces coordonnées sont généralement spécifiées dans le système nommé WGS 84 (World Geodetic System, version de 1984), utilisé entre autres par les récepteurs GPS.
Dans ce système, la longitude est comprise entre -180° et +180°, la longitude 0 étant celle du méridien origine, qui passe près de l'observatoire de Greenwich en Angleterre. La latitude d'un point est quant à elle comprise entre -90° et +90°, la latitude 0 étant celle de l'équateur. La figure ci-dessous illustre ces conventions.
Les coordonnées géographiques sont un exemple de ce que l'on nomme des coordonnées sphériques, que l'on peut voir comme une généralisation à trois dimensions des coordonnées polaires. De telles coordonnées conviennent particulièrement bien pour décrire la position de points se trouvant à la surface d'une sphère. La Terre étant (presque) sphérique, il n'est pas surprenant que ce type de coordonnées se soit imposé.
2.3. Projection Web Mercator
Le fait que la Terre soit sphérique implique qu'il n'est pas directement possible de la représenter sur la surface plane d'une carte. Il est donc nécessaire de la projeter dans le plan, au moyen d'une projection cartographique.
La projection utilisée par OpenStreetMap est généralement connue sous le nom de Web Mercator. Comme son nom l'indique, il s'agit d'une variante de la célèbre projection de Mercator, fréquemment utilisée pour les cartes mondiales. L'image ci-dessous montre une grande partie de la Terre projetée au moyen de cette projection.
La projection de Mercator a la caractéristique de ne pas permettre la représentation des pôles, car elle les projette à l'infini. Pour cette raison, les cartes l'utilisant sont toujours tronquées à partir d'une latitude donnée, comme celle ci-dessus.
De plus, la projection de Mercator est souvent critiquée, à raison, pour les importantes déformations qu'elle introduit dans les éléments situés aux latitudes élevées. Ainsi, la carte ci-dessus donne l'impression que le Groenland est aussi grand que l'Afrique, alors que cette dernière est en réalité 14 fois plus grande. La page Wikipedia consacrée à la projection de Mercator inclut une animation permettant de bien se rendre compte des déformations introduites, que les personnes intéressées pourront consulter.
2.4. Niveaux de zoom
Contrairement aux cartes physiques imprimées sur papier, qui sont établies à une échelle fixe, les cartes électroniques comme OpenStreetMap sont disponibles à plusieurs échelles. Lorsqu'on consulte de telles cartes, on peut librement passer d'une échelle à l'autre, par exemple au moyen des boutons intitulés + et -.
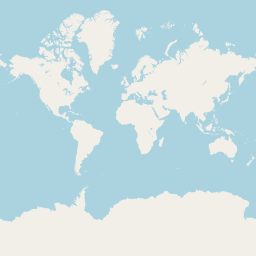
OpenStreetMap nomme niveaux de zoom (zoom levels) les différentes échelles. Le niveau 0 correspond à la plus grande échelle à laquelle la carte est disponible, et la figure 2 présente le monde à cette échelle-là. Comme on le devine, cette image est parfaitement carrée, et fait exactement 256 (28) pixels de côté.
Au niveau de zoom 1, la carte du monde d'OpenStreetMap est exactement deux fois plus grande qu'au niveau de zoom 0, dans chaque dimension. Il s'agit donc d'une image faisant 512 (29) pixels de côté, visible ci-dessous.
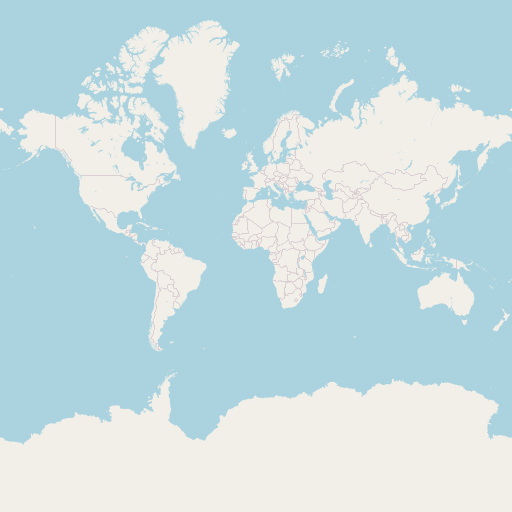
En examinant les différences entre les cartes aux niveaux de zoom 0 et 1, on constate que la seconde n'est pas simplement un agrandissement de la première. Par exemple, les frontières des pays sont visibles au niveau 1, mais pas au niveau 0.
Au niveau de zoom 2, la carte est à nouveau deux fois plus grande dans chaque dimension, et il s'agit donc d'une image de 1024 pixels de côté. Et ainsi de suite jusqu'au niveau de zoom maximum, qui vaut généralement 19. La carte du monde est alors une image de 227 pixels (plus de 134 millons) de côté.
2.5. Formules de projection
Afin de pouvoir placer sur une carte un point dont on connaît les coordonnées géographiques, il faut connaître les formules de projection. Ces formules donnent les coordonnées cartésiennes (x, y) d'un point sur la carte au niveau de zoom z, en fonction de ses coordonnées géographiques (λ, φ), exprimées en radians (!) :
\begin{align} \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} x & = 2^{8+z}\left(\frac{\lambda}{2\pi} + \frac{1}{2}\right)\\[0.5em] y & = 2^{8+z}\left(-\frac{\arsinh(\tan\phi)}{2\pi} + \frac{1}{2}\right) \end{align}Attention au fait que le système de coordonnées cartésien de la carte est celui généralement utilisé pour les images en informatique. C'est-à-dire que son origine se trouve dans le coin haut-gauche de l'image, l'axe des abscisses (x) pointe vers la droite et celui des ordonnées (y) vers le bas !
Par exemple, le coin nord-ouest du Learning Center, dont les coordonnées géographiques sont (λ = 6.56725°, φ = 46.51889°), se trouve à la position suivante dans l'image de la figure 3 — notez bien que la longitude et la latitude sont exprimés en radians ici, comme demandé par les formules :
\begin{align} \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} x & = 2^{8+1}\left(\frac{0.114620}{2\pi} + \frac{1}{2}\right) \approx 265.34 \\[0.5em] y & = 2^{8+1}\left(-\frac{\arsinh\left(\tan\left(0.811908\right)\right)}{2\pi} + \frac{1}{2}\right) \approx 181.08 \end{align}soit légèrement à droite et au-dessus du centre de l'image, ce qui semble correct.
2.6. Unités
Notre programme devra manipuler un grand nombre de données diverses liées aux aéronefs, comme leur altitude, leur vitesse, leur direction, etc. La question se pose donc de savoir quelles unités utiliser pour ces différentes données.
Il est en effet capital de choisir une et une seule unité pour chaque type de données à représenter. Sans cela, le risque est trop grand de combiner involontairement des données exprimées dans différentes unités et d'obtenir des valeurs incorrectes. 1
Nous adopterons donc la règle suivante : les données d'un certain type (angle, longueur, vitesse, etc.) manipulées par le programme seront autant que possible exprimées dans une seule unité, appelée l'unité de base. La principale exception à cette règle sont les données échangées avec le monde extérieur, qui doivent dans certains cas être exprimés dans d'autres unités.
Nous avons décidé d'utiliser les unités du système métrique comme unités de base. En conséquence, nous devrons convertir la plupart des valeurs reçues dans les messages envoyés par les aéronefs, qui sont généralement exprimées dans le système impérial, d'usage en aéronautique. De même, nous devrons parfois convertir dans d'autres unités les valeurs afin de les afficher de manière plus agréable pour l'utilisateur.
2.6.1. Angles
L'unité de base que nous utiliserons pour les angles est le radian. Il s'agit de l'unité utilisée par les fonctions trigonométriques de la bibliothèque Java, et il ne sera donc pas nécessaire d'effectuer de conversion lors de leur utilisation.
En plus du radian, les unités données dans la table ci-dessous seront nécessaires dans différentes parties du projet pour représenter les angles.
| Nom | Abréviation | Définition |
|---|---|---|
| radian (radian) | rad | — |
| tour (turn) | turn | 2π rad |
| degré (degree) | deg ou ° | turn / 360 |
| T32 | t32 | turn / 232 |
La dernière de ces unités, que nous avons choisi d'appeler T32, n'est pas couramment utilisée, mais est intéressante pour représenter les longitudes — et les latitudes, dans une moindre mesure — au moyen d'entiers de 32 bits. En effet, en exprimant un angle dans cette unité et en le représentant au moyen d'un entier signé de 32 bits, on couvre exactement la plage allant de -180° (inclus) à +180° (exclu), car :
\begin{align} -2^{31}\ \textrm{t32} &= -2^{31}\frac{\textrm{turn}}{2^{32}} = -\frac{1}{2}\textrm{turn} = -180°\\ (2^{31} - 1)\ \textrm{t32} &= (2^{31} - 1)\frac{\textrm{turn}}{2^{32}} = \frac{2^{31} - 1}{2^{32}}\textrm{turn} \approx 179.9999999° \end{align}La précision est de plus excellente — inférieure à 1 cm — car la Terre à l'équateur a une circonférence d'environ 40 000 km, ce qui implique que la différence entre deux longitudes représentées de cette manière correspond à :
\[ \frac{40\,000\ \textrm{km}}{2^{32}} \approx 0.93\ \textrm{cm} \]
Pour cette raison, cette représentation des longitudes et des latitudes, parfois nommée angular weighted binary (AWB), est utilisée, entre autres, dans les récepteurs GPS.
2.6.2. Temps
L'unité de base que nous utiliserons pour représenter le temps est la seconde. Nous utiliserons de plus parfois d'autres unités dérivées, indiquées dans la table ci-dessous.
| Nom | Abréviation | Définition |
|---|---|---|
| seconde (second) | s | — |
| minute (minute) | min | 60 s |
| heure (hour) | hr | 60 min |
2.6.3. Longueur
L'unité de base que nous utiliserons pour représenter les longueurs est le mètre. Nous utiliserons de plus parfois d'autres unités dérivées, indiquées dans la table ci-dessous.
| Nom | Abréviation | Définition |
|---|---|---|
| mètre (meter) | m | — |
| centimètre (centimeter) | cm | 10-2 m |
| kilomètre (kilometer) | km | 103 m |
| pouce (inch) | in | 2.54 cm |
| pied (foot) | ft | 12 in |
| mile nautique (nautical mile) | nmi | 1852 m |
Notez que deux des unités dérivées sont obtenues en préfixant l'unité de base au moyen d'un préfixe du système international d'unités (SI). Les préfixes utilisés ici sont :
- centi-, qui vaut 10-2,
- kilo-, qui vaut 103.
2.6.4. Vitesse
L'unité de base que nous utiliserons pour représenter les vitesses est le mètre par seconde, c.-à-d. l'unité de base des longueurs divisée par celle des durées. Nous utiliserons de plus parfois d'autres unités dérivées, indiquées dans la table ci-dessous.
| Nom | Abréviation | Définition |
|---|---|---|
| mètre par seconde (meter per second) | m/s | m / s |
| nœud (knot) | knot | nmi / hr |
| kilomètre par heure (kilometer per hour) | km/h | km / hr |
3. Mise en œuvre Java
Les concepts importants pour cette étape ayant été introduits, il est temps de décrire leur mise en œuvre en Java. En plus des classes spécifiques à cette étape, une classe « utilitaire » est à réaliser : Preconditions, qui offre une méthode de validation d'argument.
Toutes les classes et interfaces de ce projet appartiendront au paquetage ch.epfl.javions — qui sera désigné par le terme paquetage principal dans les descriptions d'étapes — ou à l'un de ses sous-paquetages.
Attention : jusqu'à l'étape 6 du projet (incluse), vous devez suivre à la lettre les instructions qui vous sont données dans l'énoncé, et vous n'avez pas le droit d'apporter la moindre modification à l'interface publique des classes, interfaces et types énumérés décrits.
En d'autres termes, vous ne pouvez pas ajouter des classes, interfaces ou types énumérés publics à votre projet, ni ajouter des attributs ou méthodes publics aux classes, interfaces et types énumérés décrits dans l'énoncé. Vous pouvez par contre définir des méthodes et attributs privés si cela vous semble judicieux.
Cette restriction sera levée dès l'étape 7.
3.1. Installation de Java et d'IntelliJ
Avant de commencer à programmer, il faut vous assurer que la version 17 de Java est bien installée sur votre ordinateur, car c'est celle qui sera utilisée pour ce projet.
Si vous ne l'avez pas encore installée, rendez-vous sur le site Web du projet Adoptium, téléchargez le programme d'installation correspondant à votre système d'exploitation (macOS, Linux ou Windows), et exécutez-le.
Cela fait, si vous n'avez pas encore installé IntelliJ, téléchargez la version Community Edition (!) depuis le site de JetBrains et installez-la.
3.2. Importation du squelette
Une fois Java et IntelliJ installés, vous pouvez télécharger le squelette de projet que nous mettons à votre disposition. Il s'agit d'une archive Zip dont vous devrez tout d'abord extraire le contenu à un emplacement de votre choix sur votre ordinateur — notez que certains navigateurs comme Safari extraient automatiquement le contenu de telles archives.
Une fois le contenu de l'archive extrait, vous constaterez qu'il se trouve en totalité dans un dossier nommé Javions. Lancez IntelliJ, choisissez Open, sélectionnez ce dossier, et finalement cliquez Ok.
Le dossier Javions contient les sous-dossiers suivants :
resources, destiné à contenir les ressources utiles au projet, et qui ne contient pour l'instant qu'un fichier nomméaircraft.zip, une base de données d'avions qui sera utile à l'étape 2,src, destiné à contenir le code source de votre projet, ainsi que divers fichiers que nous mettrons à votre disposition, et qui contient pour l'instant :SignatureChecks_1.java, un fichier de vérification de signatures pour l'étape 1, qui ne devrait plus contenir d'erreur lorsque vous aurez terminé la rédaction de cette étape,Submit.java, un programme qui vous permettra de rendre votre projet à la fin de chaque semaine,
test, destiné à contenir le code des tests unitaires de votre projet que nous vous fournirons ou que vous écrirez vous-même, et qui contient pour l'instant les tests de l'étape 1 — fournis exceptionnellement pour faciliter votre démarrage.
Le dossier resource doit être marqué comme « dossier de ressources » pour qu'il soit correctement géré par IntelliJ. Pour cela, faites un clic droit sur lui puis sélectionnez Mark Directory As puis Resources Root. Vérifiez ensuite que le panneau Project d'IntelliJ ressemble à l'image ci-dessous.
3.3. Classe Preconditions
Fréquemment, les méthodes d'un programme demandent que leurs arguments satisfassent certaines conditions. Par exemple, une méthode déterminant la valeur maximale d'un tableau d'entiers exige que ce tableau contienne au moins un élément.
De telles conditions sont souvent appelées préconditions (preconditions) car elles doivent être satisfaites avant l'appel d'une méthode : c'est à l'appelant de s'assurer qu'il n'appelle la méthode qu'avec des arguments valides.
En Java, la convention veut que chaque méthode vérifie, autant que possible, ses préconditions et lève une exception — souvent IllegalArgumentException — si l'une d'entre elles n'est pas satisfaite. Par exemple, une méthode max calculant la valeur maximale d'un tableau d'entiers, et exigeant logiquement que celui-ci contienne au moins un élément, pourrait commencer ainsi :
int max(int[] array) {
if (! (array.length > 0))
throw new IllegalArgumentException();
// … reste du code
}
(Notez au passage que la méthode max ne déclare pas qu'elle lève potentiellement IllegalArgumentException au moyen d'une clause throws, car cette exception est de type unchecked.)
La première classe à réaliser dans le cadre de ce projet a pour but de faciliter l'écriture de telles préconditions. En l'utilisant, la méthode ci-dessus pourrait être simplifiée ainsi :
int max(int[] array) {
Preconditions.checkArgument(array.length > 0);
// … reste du code
}
Cette classe est nommée Preconditions et appartient au paquetage principal. Elle est publique et finale et n'offre rien d'autre que la méthode checkArgument décrite plus bas. Elle a toutefois la particularité d'avoir un constructeur par défaut privé :
public final class Preconditions {
private Preconditions() {}
// … méthodes
}
Le but de ce constructeur privé est de rendre impossible la création d'instances de la classe, puisque cela n'a clairement aucun sens — elle ne sert que de conteneur à une méthode statique. Dans la suite du projet, nous définirons plusieurs autres classes du même type, que nous appellerons dès maintenant classes non instanciables.
La méthode publique (et statique) offerte par la classe Preconditions est :
void checkArgument(boolean shouldBeTrue), qui lève l'exceptionIllegalArgumentExceptionsi son argument est faux, et ne fait rien sinon.
3.4. Classe Units
La classe Units du paquetage principal, publique, finale et non instanciable, contient la définition des préfixes SI utiles au projet, des classes imbriquées contenant les définitions des différentes unités, ainsi que des méthodes de conversion.
Les préfixes SI sont définis comme des constantes — c.-à-d. des attributs publics, statiques et finaux — de type double, nommées CENTI et KILO, dont la valeur est celle du préfixe.
Les unités sont également des constantes de type double, mais elles sont définies dans l'une des quatre classes non instanciables suivantes, qui sont chacune imbriquées statiquement dans la classe Units :
Anglecontient les définitions des unités d'angle :RADIAN,TURN,DEGREEetT32,Lengthcontient les définitions des unités de longueur :METER,CENTIMETER,KILOMETER,INCH,FOOTetNAUTICAL_MILE,Timecontient les définitions des unités de temps :SECOND,MINUTEetHOUR,Speedcontient les définitions des unités de vitesse :KNOTetKILOMETER_PER_HOUR.
Dans chacun des cas, l'unité de base (radian, mètre, etc.) est définie comme une constante valant 1. Les autres unités sont définies en fonction de l'unité de base ou d'autres unités précédentes, de la même manière que dans les tables de la §2.6.
Grâce à ces définitions, la conversion d'une valeur depuis une unité de départ vers une unité d'arrivée se fait simplement en multipliant la valeur par le rapport entre l'unité d'arrivée est celle de départ. Dans un soucis de clareté, les méthodes (statiques) suivantes sont définies par Units dans ce but :
double convert(double value, double fromUnit, double toUnit), qui convertit la valeur donnée, exprimée dans l'unitéfromUnit, en l'unitétoUnit,double convertFrom(double value, double fromUnit), équivalente àconvertlorsque l'unité d'arrivée (toUnit) est l'unité de base et vaut donc 1,double convertTo(double value, double toUnit), équivalente àconvertlorsque l'unité de départ (fromUnit) est l'unité de base et vaut donc 1.
Par exemple, l'expression suivante convertit 2 pieds en centimètres, et vaut donc 60.96 :
Units.convert(2, Units.Length.FOOT, Units.Length.CENTIMETER)
3.4.1. Conseils de programmation
- Organisation de la classe
Comme cela est mentionné ci-dessus, les classes contenant les unités des différentes dimensions sont imbriquées statiquement dans la classe
Units, dont la structure est donc la suivante :public final class Units { private Units() {} public static final double CENTI = 1e-2; // … autre(s) préfixe(s) SI utile(s) au projet // … classe Angle public static class Length { private Length() {} public static final double METER = 1; public static final double CENTIMETER = CENTI * METER; // … autres unités de longueur } // … classes Time et Speed, méthodes de conversion }Cet exemple illustre également le fait que Java autorise l'utilisation de la notation scientifique pour les valeurs de type
double, ce qui permet de définir le préfixeCENTIcomme1e-2, qui signifie 10-2. - Conversion
La conversion d'une valeur entre deux unités s'effectue en multipliant la valeur par le rapport des unités. Lorsque vous écrivez le code correspondant, utilisez des parenthèses pour forcer le calcul de ce rapport à être fait avant la multiplication de la valeur. Par exemple, le code pour convertir x pieds en centimètres devrait être écrit ainsi :
x * (Units.Length.FOOT / Units.Length.CENTIMETER)
plutôt que simplement ainsi :
x * Units.Length.FOOT / Units.Length.CENTIMETER
L'avantage de la première solution est que, comme les constantes représentant les unités (
FOOTetCENTIMETERici) sont justement des constantes, leur rapport peut être précalculé par Java, et seule la multiplication reste à effectuer au moment de l'exécution. Cela rend la conversion plus rapide qu'avec la seconde solution, qui implique une multiplication suivie d'une division.(On pourrait penser que Java peut automatiquement récrire la première version en la seconde, car les expressions sont mathématiquement équivalentes. Ce n'est malheureusement pas le cas, car lorsqu'elles sont calculées avec des valeurs de type
double, à précision limitée, elles ne sont pas tout à fait équivalentes et la transformation est donc interdite.)Notez que ce conseil est également valable pour la méthode
convertTo, dans laquelle la division doit être exprimée comme une multiplication par l'inverse de la constante représentant l'unité d'arrivée. - Multiplications/divisions par des puissances de deux
La définition de certaines unités, par exemple T32, nécessite la multiplication ou la division d'une valeur par une puissance de 2. Pour faire de telles multiplications ou divisions, prenez l'habitude d'utiliser la méthode
scalbdeMath, qui permet de calculer \(x\times 2^y\) en écrivant simplementMath.scalb(x, y).L'utilisation de cette méthode permet d'une part souvent de rendre le programme plus concis, et améliore d'autre part son efficacité.
3.5. Classe Math2
La classe Math2, du paquetage principal, publique, finale et non instanciable, offre des méthodes statiques permettant d'effectuer certains calculs mathématiques. Elle est donc similaire à la classe Math de la bibliothèque standard Java.
En plus de son constructeur privé, cette classe offre les méthodes publiques (et statiques) suivantes :
int clamp(int min, int v, int max), qui limite la valeurvà l'intervalle allant deminàmax, en retournantminsivest inférieure àmin,maxsivest supérieure àmax, etvsinon ; lèveIllegalArgumentExceptionsiminest (strictement) supérieur àmax,double asinh(double x), qui retourne le sinus hyperbolique réciproque de son argumentx(voir les conseils de programmation plus bas),
Notez que ces méthodes ne seront pas forcément utiles dans cette étape. Ne vous en faites donc pas si vous ne les utilisez pas immédiatement.
3.5.1. Conseils de programmation
Le sinus hyperbolique réciproque peut se calculer ainsi :
\[ \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} \arsinh x = \ln\left( x + \sqrt{1 + x^2}\,\right) \]
où \(\ln\) est le logarithme naturel, qui s'obtient au moyen de la méthode log de la classe Math.
Il faut noter qu'en mathématiques, le sinus hyperbolique réciproque est normalement noté arsinh, alors qu'en informatique il est généralement noté asinh (sans r). C'est ce dernier nom que nous avons choisi d'utiliser pour la méthode de la classe Math2.
3.6. Enregistrements Java
Avant de décrire GeoPos, la prochaine classe à mettre en œuvre pour cette étape, il convient de décrire le concept de classe enregistrement (record class), ou simplement enregistrement (record). Ce type de classe a été introduit très récemment en Java, avec la version 17 du langage.
Un enregistrement est un type particulier de classe qui peut se définir au moyen d'une syntaxe plus concise qu'une classe normale. Dans cette syntaxe, le mot-clef class est remplacé par record et les attributs de la classe sont donnés entre parenthèses, après son nom.
Par exemple, un enregistrement nommé Complex représentant un nombre complexe dont les attributs sont sa partie réelle re et sa partie imaginaire im peut se définir ainsi :
public record Complex(double re, double im) { }
Cette définition est équivalente à celle d'une classe finale (!) dotée de :
- deux attributs privés et finaux nommés
reetim, - un constructeur prenant en argument la valeur de ces attributs et les initialisant,
- des méthodes d'accès (getters) publics nommés
re()etim()pour ces attributs, - une méthode
equalsretournant vrai si et seulement si l'objet qu'on lui passe est aussi une instance deComplexet que ses attributs sont égaux à ceux dethis, - une méthode
hashCodecompatible avec la méthodeequals— le but de cette méthode et la signification de sa compatibilité avecequalsseront examinés ultérieurement dans le cours, - une méthode
toStringretournant une chaîne composée du nom de la classe et du nom et de la valeur des attributs de l'instance, p. ex.Complex[re=1.0, im=2.0].
En d'autres termes, la définition plus haut, qui tient sur une ligne, est équivalente à la définition suivante, qui n'utilise que des concepts que vous connaissez déjà :
public final class Complex {
private final double re;
private final double im;
public Complex(double re, double im) {
this.re = re;
this.im = im;
}
public double re() { return re; }
public double im() { return im; }
@Override
public boolean equals(Object that) {
// … vrai ssi that :
// 1. est aussi une instance de Complex, et
// 2. ses attributs re et im sont identiques.
}
@Override
public int hashCode() {
// … code omis car peu important
}
@Override
public String toString() {
return "Complex[re=" + re + ", im=" + im + "]";
}
}
Comme cet exemple l'illustre, les enregistrements permettent d'éviter d'écrire beaucoup de code répétitif, ce que les anglophones appellent du boilerplate code. Il faut toutefois bien comprendre qu'en dehors d'une syntaxe très concise, les enregistrements n'apportent — pour l'instant en tout cas — rien de nouveau à Java, dans le sens où il est toujours possible de récrire un enregistrement en une classe Java équivalente, comme ci-dessus. En cela, les enregistrements sont similaires aux types énumérés (enums).
Il est bien entendu possible de définir des méthodes dans un enregistrement, qui viennent s'ajouter à celles définies automatiquement. Par exemple, pour doter l'enregistrement Complex d'une méthode modulus retournant son module, il suffit de l'ajouter entre les accolades, ainsi :
public record Complex(double re, double im) {
public double modulus() { return Math.hypot(re, im); }
}
(La méthode Math.hypot(x,y) retourne \(\sqrt{x^2 + y^2}\) ).
Finalement, il est aussi possible de définir ce que l'on nomme un constructeur compact (compact constructor), qui augmente le constructeur que Java ajoute par défaut aux enregistrements. Un constructeur compact doit son nom au fait qu'il semble ne prendre aucun argument, et n'initialise pas explicitement les attributs. En réalité, il prend des arguments qui sont les mêmes que ceux de l'enregistrement (re et im dans notre exemple), et Java lui ajoute automatiquement des affectations de ces arguments aux attributs correspondants.
Par exemple, on pourrait vouloir ajouter un constructeur compact à la classe Complex pour lever une exception si l'un des arguments passés au constructeur était une valeur NaN (not a number, une valeur invalide). On pourrait le faire ainsi :
public record Complex(double re, double im) {
public Complex { // constructeur compact
if (Double.isNaN(re) || Double.isNaN(im))
throw new IllegalArgumentException();
}
// … méthode modulus
}
Ce constructeur compact serait automatiquement traduit ainsi :
public final class Complex {
// … attributs re et im
public Complex(double re, double im) {
if (Double.isNaN(re) || Double.isNaN(im))
throw new IllegalArgumentException();
this.re = re; // ajouté automatiquement
this.im = im; // ajouté automatiquement
}
// … méthodes modulus, re, im, hashCode, etc.
}
Les enregistrements ne seront pas décrits en détail dans le cours, mais seront introduits au moyen d'exemples similaires à ceux ci-dessus dans la suite du projet. Les personnes intéressées par les détails de leur fonctionnement pourront se rapporter à la §8.10 (Record Classes) de la spécification du langage.
3.7. Enregistrement GeoPos
L'enregistrement GeoPos du paquetage principal, public, représente des coordonnées géographiques, c.-à-d. un couple longitude/latitude. Ces coordonnées sont exprimées en t32 et stockées sous la forme d'entiers de 32 bits (type int).
Les attributs de GeoPos sont donc :
int longitudeT32, la longitude exprimée en t32,int latitudeT32, la latitude exprimée en t32.
L'enregistrement GeoPos offre une méthode publique et statique :
boolean isValidLatitudeT32(int latitudeT32), qui retourne vrai ssi la valeur passée, interprétée comme une latitude exprimée en t32, est valide, c.-à-d. comprise entre -230 (inclus, et qui correspond à -90°) et 230 (inclus, et qui correspond à +90°).
Cette méthode est utilisée, entre autres, par le constructeur compact de GeoPos pour valider la latitude reçue et lever IllegalArgumentException si elle est invalide.
En plus des méthodes publiques définies automatiquement pour les enregistrements, GeoPos offre les deux méthodes publiques suivantes :
double longitude(), qui retourne la longitude (en radians !),double latitude(), qui retourne la latitude (en radians !).
Finalement, GeoPos contient une redéfinition de la méthode toString de Object qui retourne une représentation textuelle de la position dans laquelle la longitude et la latitude sont données dans cet ordre, en degrés (!). Par exemple, l'extrait de code ci-dessous devrait afficher (82.784228855744°, 10.34802851267159°) :
System.out.println(new GeoPos(987654321, 123456789))
La classe GeoPos illustre une convention que nous adopterons dans la suite du projet pour nommer les différentes entités — variables, attributs ou méthodes — contenant des valeurs exprimées dans une unité donnée : un suffixe constitué de l'abréviation de l'unité sera ajouté au nom de l'entité, sauf si l'unité est celle de base.
C'est pour cette raison que les attributs longitudeT32 et latitudeT32 ont un nom se terminant par T32, alors que le suffixe Rad n'est pas attaché au nom des méthodes longitude et latitude.
3.8. Classe WebMercator
La classe WebMercator du paquetage principal, publique et non instanciable, contient des méthodes (statiques) permettant de projeter des coordonnées géographiques selon la projection WebMercator. Il s'agit de :
double x(int zoomLevel, double longitude), qui retourne la coordonnée x correspondant à la longitude donnée (en radians) au niveau de zoom donné,double y(int zoomLevel, double latitude), qui retourne la coordonnée y correspondant à la latitude donnée (en radians) au niveau de zoom donné.
Notez que même si, en pratique, le niveau de zoom devrait être compris entre 0 et 19 (voir 20), les formules de projection fonctionnent même avec d'autres valeurs. Pour cette raison, aucune tentative de validation du niveau de zoom n'est faite.
3.8.1. Conseils de programmation
Les formules données à la §2.5 contiennent des divisions par 2π que l'on peut voir comme des conversions d'angles exprimés en radians en angles exprimés en tours. Il est donc raisonnable d'utiliser la méthode convertTo de Units pour les effectuer.
3.9. Classe Bits
La classe Bits du paquetage principal, publique et non instanciable, contient des méthodes permettant d'extraire un sous-ensemble des 64 bits d'une valeur de type long. Ces méthodes sont :
int extractUInt(long value, int start, int size), qui extrait du vecteur de 64 bitsvaluela plage desizebits commençant au bit d'indexstart, qu'elle interprète comme une valeur non signée, ou lève :IllegalArgumentExceptionsi la taille n'est pas strictement supérieure à 0 et strictement inférieure à 32, ouIndexOutOfBoundsExceptionsi la plage décrite parstartetsizen'est pas totalement comprise entre 0 (inclus) et 64 (exclu),
boolean testBit(long value, int index), qui retourne vrai ssi le bit devalued'index donné vaut 1, ou lèveIndexOutOfBoundsExceptions'il n'est pas compris entre 0 (inclus) et 64 (exclu).
Souvenez-vous que les bits sont numérotés de droite à gauche, le bit le plus à droite ayant l'index 0.
3.9.1. Conseils de programmation
La validation des arguments des deux méthodes peut être considérablement simplifiée par l'utilisation des méthodes checkFromIndexSize et checkIndex de la classe Objects (avec un s).
Plutôt que de passer directement les constantes 32 ou 64 à ces méthodes, utilisez les attributs Integer.SIZE et Long.SIZE pour rendre votre code plus clair.
3.10. Classe ByteString
La classe ByteString du paquetage principal, publique et finale, représente une chaîne (séquence) d'octets. Ses instances sont très similaires à un tableau de type byte[], à deux différences près :
ByteStringest immuable, donc il n'est pas possible de changer les octets qu'une instance contient une fois qu'elle a été créée, et- ces octets sont interprétés de manière non signée.
La classe ByteString offre un unique constructeur public :
ByteString(byte[] bytes), qui retourne une chaîne d'octets dont le contenu est celui du tableau passé en argument.
Pour faciliter la construction de chaînes d'octets à partir de leur représentation hexadécimale, elle offre également la méthode statique suivante :
ByteString ofHexadecimalString(String hexString), qui retourne la chaîne d'octets dont la chaîne passée en argument est la représentation hexadécimale, ou lève une exception de typeIllegalArgumentException(ouNumberFormatException, qui en est un sous-type) si la chaîne donnée n'est pas de longueur paire, ou si elle contient un caractère qui n'est pas un chiffre hexadécimal (voir les conseils de programmation plus bas).
La classe ByteString offre également les méthodes publiques suivantes :
int size(), qui retourne la taille de la chaîne, c.-à-d. le nombre d'octets qu'elle contient,int byteAt(int index), qui retourne l'octet (interprété en non signé) à l'index donné, ou lèveIndexOutOfBoundsExceptionsi celui-ci est invalide,long bytesInRange(int fromIndex, int toIndex), qui retourne les octets compris entre les indexfromIndex(inclus) ettoIndex(exclu) sous la forme d'une valeur de typelong, l'octet d'indextoIndex - 1constituant l'octet de poids faible du résultat, ou lève :IndexOutOfBoundsExceptionsi la plage décrite parfromIndexettoIndexn'est pas totalement comprise entre 0 et la taille de la chaîne,IllegalArgumentExceptionsi la différence entretoIndexetfromIndexn'est pas strictement inférieure au nombre d'octets contenus dans une valeur de typelong.
L'ordre dans lequel bytesInRange place les octets dans la valeur de type long retournée peut sembler étrange mais est assez naturel, comme illustré par l'extrait de programme suivant, qui affiche true :
ByteString b = ByteString.ofHexadecimalString("ABCDEF0102");
System.out.println(b.bytesInRange(1,3) == 0xCDEF);
Finalement, ByteString redéfinit trois méthodes de Object, qui sont :
equals, qui retourne vrai ssi la valeur qu'on lui passe est aussi une instance deByteStringet que ses octets sont identiques à ceux du récepteur (voir les conseils de programmation plus bas),hashCode, qui retourne la valeur retournée par la méthodehashCodedeArraysappliquée au tableau contenant les octets,toString, qui retourne une représentation des octets de la chaîne en hexadécimal, chaque octet occupant exactement deux caractères.
3.10.1. Conseils de programmation
- Constructeur
La classe
ByteStringdoit être immuable, ce qui implique que le tableau passé au constructeur ne peut pas être stocké directement dans un attribut de la classe. Au lieu de cela, c'est une copie de ce tableau, obtenue par exemple avec la méthodeclone, qui doit être stockée. - Méthodes
ofHexadecimalStringettoString
L'écriture des méthodes
ofHexadecimalStringettoStringpeut être simplifiée par l'utilisation d'une instance de la classeHexFormatde la bibliothèque Java. Son but est de faciliter la conversion entre des séquences d'octets et leur représentation textuelle. L'extrait de programme ci-dessous illustre l'utilisation de cette classe, et vous pouvez vous en inspirer pour écrire la classeByteString.HexFormat hf = HexFormat.of().withUpperCase(); byte[] bytes = new byte[]{ (byte)0x01, (byte)0xAB }; String string = hf.formatHex(bytes); // vaut "01AB" byte[] bytes2 = hf.parseHex(string); // identique à bytes System.out.println(Arrays.equals(bytes, bytes2)); // true - Méthode
bytesInRange
Pour valider les index passés à la méthode
bytesInRange, vous pouvez utiliser la méthodecheckFromToIndexde la classeObjects. - Filtrage de motif avec
instanceof
Comme vous le savez, la méthode
equalsreçoit un argument de typeObject. Dès lors, toute redéfinition de cette méthode commence toujours par vérifier si l'objet reçu a bien le même type que le récepteur au moyen de l'opérateurinstanceof, puis si c'est le cas, effectue un transtypage. Par exemple, la méthodeequalsdeByteStringpourrait commencer ainsi :public boolean equals(Object thatO) { if (thatO instanceof ByteString) { ByteString that = (ByteString)thatO; // … utilise that } else // … }Il est fastidieux de devoir écrire ce genre de code dans chaque méthode
equals, et Java offre donc depuis peu une syntaxe abrégée qui permet de combiner le testinstanceofet la déclaration de la variable transtypée (thatci-dessus) en une seule opération, ainsi :public boolean equals(Object thatO) { if (thatO instanceof ByteString that) { // … utilise that } else // … }Notez bien le
thatqui suit leByteStringdans le testinstanceof, et qui déclare la variablethat.En anglais, cette syntaxe est appelée pattern matching for
instanceof, que l'on pourrait traduire par « filtrage de motifs pourinstanceof». Il s'agit d'un cas particulier de filtrage de motifs (pattern matching), une construction très utile en programmation, qui constitue l'une des caractéristiques des langages de programmation dits fonctionnels. Le filtrage de motifs est en cours d'ajout à Java, et nous en rencontrerons une autre utilisation plus tard dans le projet. - Méthodes
equalsethashCode
La méthode
equalsdoit comparer le contenu du tableau d'octets du récepteur avec celui du tableau d'octets passé en argument. Pour ce faire, il n'est pas correct d'appliquer directement la méthodeequalsde l'un des deux tableaux, car les tableaux sont comparés par référence en Java. Pour comparer leur contenu — ce qui est le but ici — il faut utiliser la méthodeequalsdeArrays.La méthode
hashCodea pour but de déterminer ce que l'on nomme la valeur de hachage (hash code) de la chaîne. La notion de valeur de hachage, et son utilité, seront décrites plus tard dans le cours. Toutefois, la méthodehashCodedeByteStringest très simple à écrire car elle doit simplement retourner la valeur retournée par la méthodehashCodedeArrays, appliquée au tableau contenant les octets de la chaîne.
3.11. Tests
Pour vous aider à démarrer ce projet, des tests unitaires JUnit vous sont exceptionnellement fournis pour cette étape, et se trouvent dans le dossier test du squelette. Une fois que vous aurez terminé la rédaction des classes de cette étape, vous pourrez les exécuter en :
- ajoutant JUnit à votre projet, comme expliqué dans notre guide à ce sujet,
- effectuant un clic droit sur le dossier
testdu projet et sélectionnant Run 'All Tests'.
3.12. Documentation
Une fois les tests exécutés avec succès, il vous reste à documenter la totalité des entités publiques (classes, attributs et méthodes) définies dans cette étape, au moyen de commentaires Javadoc, comme décrit dans le guide consacré à ce sujet. Vous pouvez écrire ces commentaires en français ou en anglais, en fonction de votre préférence, mais vous ne devez utiliser qu'une seule langue pour tout le projet.
4. Résumé
Pour cette étape, vous devez :
- installer la version 17 (et ni une plus récente, ni une plus ancienne !) de Java sur votre ordinateur, ainsi que la dernière version d'IntelliJ,
- écrire les classes
Preconditions,Units(classes imbriquées incluses),Math2,GeoPos,WebMercator,BitsetByteStringselon les indications ci-dessus, - vérifier que les tests que nous vous fournissons s'exécutent sans erreur, et dans le cas contraire, corriger votre code,
- documenter la totalité des entités publiques que vous avez définies,
- (optionnel mais fortement recommandé) rendre votre code au plus tard le 24 février 2023 à 18h00, en exécutant le programme
Submitfourni dans le squelette, après avoir modifié les définitions des variablesTOKEN_1etTOKEN_2pour qu'elles contiennent les jetons individuels des deux membres du groupe, disponibles sur la page privée de chacun d'eux.
Ce premier rendu n'est pas noté, mais celui de la prochaine étape le sera. Dès lors, il est vivement conseillé de faire un rendu de test cette semaine afin de se familiariser avec la procédure à suivre.
Notes de bas de page
L'utilisation erronée d'unités différentes dans des programmes informatiques a déjà causé de très nombreux et coûteux accidents, comme par exemple la perte de la sonde spatiale Mars Climate Orbiter de la NASA en 1999. Pour cette raison, quelques — trop rares — langages de programmation comme F# offrent la possibilité d'attacher des unités aux valeurs manipulées, et signalent les calculs combinant de manière incorrecte des valeurs exprimées dans des unités incompatibles. Ce n'est malheureusement pas le cas de Java, raison pour laquelle il est capital de n'utiliser qu'une unité de manière aussi systématique que possible.