Ensemble par hachage préservant l'ordre

CS-108 — Série 12

Introduction

Comme nous l'avons vu au cours, les collections de la bibliothèque Java basées sur le hachage — HashSet et HashMap — ont l'inconvénient de fournir leurs éléments dans un ordre difficilement prévisible lors d'un parcours.

Le but de cette série est d'écrire une mise en œuvre des ensembles basée sur une table de hachage, mais dont l'ordre de parcours soit celui d'insertion. De plus, cette mise en œuvre n'utilisera pas de listes pour stocker les éléments se trouvant à la même position dans la table — grâce à une technique nommée adressage ouvert (open addressing).

Dès lors, la mise en œuvre de cette série diffère de celle vue au cours (SHashSet) en deux points :

plutôt que d'être stockés directement dans la table de hachage, les éléments sont stockés dans un tableau (dynamique), en ordre d'insertion, et c'est leur index dans ce tableau qui est stocké dans la table de hachage,
plutôt que la table de hachage soit constituée de listes contenant chacune un petit nombre (d'index) d'éléments, ceux-ci sont directement stockés dans la prochaine position libre de la table — c'est l'idée de l'adressage ouvert.

Ces deux différences sont illustrées dans les sections suivantes, au moyen d'un ensemble de chaînes de caractères contenant les noms des quatre premiers jours de la semaine. Pour simplifier la discussion, nous ferons l'hypothèse que la valeur de hachage de ces chaînes, produite par leur méthode hashCode, est celle de la colonne h de la table ci-dessous — les colonnes h3 et h2 donnant les 3 et 2 bits de poids faible de h, qui seront utiles ultérieurement :

Chaîne	`h`	`h3`	`h2`
lundi	74	2	2
mardi	99	3	3
mercredi	65	1	1
jeudi	31	7	3

Dans un premier temps, admettons que l'on ajoute ces 4 chaînes, dans l'ordre ci-dessus, à un ensemble de type SHashSet dont la table de hachage est composée de 4 listes. La position des chaînes dans la table serait alors déterminée par les deux bits de poids faible de leur valeur de hachage, qui figurent dans la colonne h2 de la table plus haut. On obtiendrait donc la situation suivante :

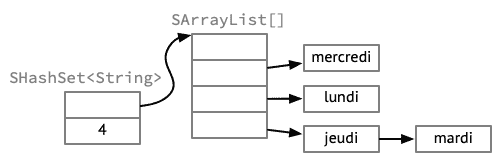
hash-1;16.png — Figure 1 : L'ensemble comme une instance de `SHashSet`

En parcourant cet ensemble, ses éléments apparaîtraient donc dans l'ordre {mercredi, lundi, jeudi, mardi}, différent de l'ordre d'insertion — et difficile à prévoir.

Préservation de l'ordre d'insertion

La raison pour laquelle les éléments d'un ensemble de type SHashSet sont parcourus dans un ordre difficile à prévoir est qu'ils le sont dans l'ordre dans lequel ils apparaissent dans la table de hachage — qui dépend non seulement de leur valeur de hachage, mais aussi de la taille de la table.

Pour résoudre ce problème, on peut stocker les éléments dans un tableau, dans l'ordre d'insertion, pour ensuite ne stocker, dans la table de hachage, que leur index dans ce tableau. La table de hachage est utilisée comme d'habitude pour toutes les opérations, sauf pour le parcours, qui est fait directement sur le tableau.

La figure ci-dessous montre comment l'ensemble décrit plus haut pourrait être représenté en utilisant cette idée.

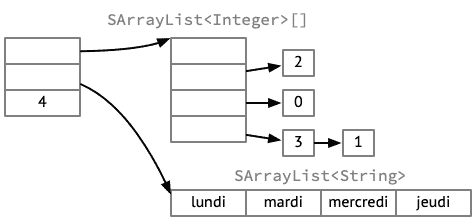
hash-2;16.png — Figure 2 : L'ensemble avec l'ordre d'insertion préservé

On voit facilement sur cette figure qu'en parcourant directement le tableau, on obtient les éléments dans leur ordre d'insertion dans l'ensemble.

Adressage ouvert

Les tables de hachage présentées plus haut sont constituées de listes qui contiennent les éléments dont la valeur de hachage, une fois réduite à un index valide, est identique.

L'idée de l'adressage ouvert est de ne pas stocker les éléments dans des listes regroupées dans une table, mais directement dans la table elle-même. Lorsqu'on désire placer un élément à un index donné et que celui-ci est déjà occupé, on regarde si la position suivante de la table est libre, et si tel est le cas, on y place l'élément ; sinon, on examine la position suivante, et ainsi de suite jusqu'à ce qu'on trouve une position libre.

La figure ci-dessous montre comment l'ensemble décrit plus haut pourrait être représenté en utilisant cette idée. La taille de la table a été doublée, pour passer à 8 éléments, car lorsqu'on utilise l'adressage ouvert, la table ne doit jamais être pleine. De plus, les emplacements inutilisés de la table ont été remplis avec une valeur invalide (–1), car il est nécessaire de pouvoir les différencier des emplacements utilisés.

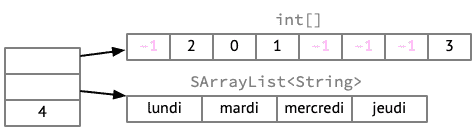
hash-3;16.png — Figure 3 : L'ensemble avec l'ordre d'insertion préservé et adressage ouvert

L'adressage ouvert consiste en quelque sorte à stocker les listes d'éléments directement dans la table, à la différence près qu'il est tout à fait possible que plusieurs listes se retrouvent combinées en une seule séquence de valeurs sans case libre entre deux, que nous appellerons un amas (cluster). Dans la figure ci-dessus, les index 2, 0 et 1, qui correspondent à mercredi, lundi et mardi, forment un tel amas.

Les amas sont problématiques car ils ralentissent toutes les opérations. Pour l'illustrer, admettons que l'on désire déterminer si la chaîne saturday se trouve dans l'ensemble, et supposons de plus que sa valeur de hachage, une fois réduite à un index valide, vaut 1. Dans ce cas, il faudrait comparer cette chaîne avec tous les éléments situés entre l'index 1 et le premier élément inoccupé, à savoir ceux situés à l'index 1 (mercredi), 2 (lundi) et 3 (mardi). Dans la version de la table basée sur les listes, une seule comparaison est nécessaire, car la liste à l'index 1 ne contient que la chaîne mardi.

De même, l'insertion de la chaîne saturday dans l'ensemble supposerait de commencer à l'index 1 en faisant les mêmes comparaisons, puis de finalement l'insérer — ou plutôt d'insérer son index dans le tableau — dans le premier emplacement libre de la table, donc à l'index 4.

Avec l'adressage ouvert, il est donc important d'essayer d'éviter la création de trop gros amas, ce qui se fait généralement en s'assurant que la table de hachage est d'une taille 2 à 4 fois plus grande que celle de l'ensemble.

Finalement, l'adressage ouvert rend la suppression d'éléments plus complexe que la solution basée sur les listes. En effet, lorsqu'un élément est supprimé d'une table utilisant l'adressage ouvert, on ne peut en général pas simplement remplacer son index par –1 dans la table, car cela risquerait de découper un amas en deux parties. Différentes solutions à ce problème existent, et l'une d'entre elles est examinée dans le cadre de l'exercice 3.

Squelette

Nous mettons à votre disposition une archive Zip contenant :

l'interface SSet et la classe SAbstractSet vues au cours,
un enregistrement (privé au paquetage) nommé Table et représentant une table de hachage dont la taille est une puissance de 2,
le squelette d'une classe nommée SOrderPreservingSet1, à compléter dans le cadre des exercices 1 et 2,
le squelette d'une classe nommée SOrderPreservingSet, à compléter dans le cadre de l'exercice 3,
des classes de test pour les deux classes à compléter.

La capacité (taille) de la table de hachage utilisée par les ensembles de cette série est toujours une puissance de 2. Cela permet d'utiliser un masquage de bits pour réduire une valeur de hachage quelconque à un index valide, ce qui est simple et rapide.

L'enregistrement Table, privé au paquetage, a pour but de simplifier la gestion de cette table. La méthode statique ofLogCapacity permet de créer une table dont la log-capacité — le logarithme en base 2 de sa capacité — est donnée en argument.

Les différentes méthodes non statiques — indexFor, get, set, etc. — facilitent l'accès aux éléments de la table. Prenez un moment pour lire leur code et les commentaires qui leur sont attachés afin de bien comprendre leur fonctionnement et leur utilité.

Exercice 1 : capacité fixe

Complétez la classe SOrderPreservingSet1 en écrivant le corps de ses méthodes size, add, contains et iterator, et en ajoutant les attributs nécesaires. Cette première version ne doit gérer ni le redimensionnement (rehachage), ni la suppression d'éléments.

Notez que la méthode iterator peut se définir très simplement, car tant et aussi longtemps que la suppression d'éléments n'est pas possible, itérer sur l'ensemble équivaut à itérer sur le tableau contenant les éléments.

Dans un soucis de simplicité, et à l'image de plusieurs collections de la bibliothèque Java, les ensembles représentés par les classes de cette série n'acceptent pas null comme élément. Dès lors, leurs méthodes add et contains peuvent utiliser requireNonNull pour lever une exception si l'élément qu'on leur passe est nul.

Une fois votre mise en œuvre terminée, lancez les tests de la classe SOrderPreservingSet1Test et vérifiez qu'ils s'exécutent avec succès.

Exercice 2 : redimensionnement

Ajoutez à votre classe une méthode privée nommée p. ex. rehashIfNeeded, qui augmente la capacité de la table si nécessaire. Ajoutez ensuite un appel à cette méthode à la fin de la méthode add.

La capacité de la table doit être augmentée si sa log-capacité actuelle n'est pas supérieure ou égale à la log-capacité idéale pour le nombre d'éléments qu'elle contient, déterminée par la méthode idealLogCapacity de Table.

Une fois votre mise en œuvre terminée, changez la définition de maxSize dans la classe de test afin qu'elle retourne 4500, puis lancez les tests et vérifiez qu'ils s'exécutent avec succès.

Exercice 3 : suppression

Complétez la classe SOrderPreseervingSet en écrivant le corps de ses méthodes size, add, contains, remove et iterator. Cette seconde version doit gérer aussi bien le rehachage que la suppression d'éléments.

Bien entendu, vous pouvez dans un premier temps copier le code des méthodes de votre classe précédente dans la nouvelle, mais notez que la suppression a un impact sur toutes les méthodes écrites jusqu'à présent, et leur code devra donc être augmenté.

La suppression d'éléments est moins simple à gérer qu'il n'y paraît, pour deux raisons :

l'élément supprimé ne peut pas simplement être supprimé du tableau des éléments, faute de quoi les index des éléments suivants changeraient, et une potentiellement grosse partie de la table devrait être modifiée,
l'index de l'élément supprimé ne peut pas simplement être supprimé de la table — c.-à-d. remplacé par –1 — car cela pourrait diviser un amas en deux, ce qui est incorrect.

Pour résoudre le premier problème, on peut simplement remplacer l'élément par null dans le tableau, préservant ainsi l'index des éléments suivants. Attention, ces éléments doivent être ignorés par l'itérateur !

Pour résoudre le second problème, on peut stocker une autre valeur spéciale — souvent appelée pierre tombale (tombstone) dans la littérature — p. ex. –2, dans l'emplacement d'un élément supprimé. Lors du parcours de la table, les emplacements contenant cette valeur ne sont pas considérés comme libres, et ne terminent donc pas l'amas auquel ils appartiennent.

Lors d'un rehachage, le tableau des éléments et la table de hachage sont « compactés » en supprimant les éléments nuls du premier et en ne copiant pas les pierres tombales de la seconde.

Finalement, afin de correctement gérer le cas où la table contient beaucoup de « pierres tombales », le nombre d'éléments utilisé pour déterminer si un rehachage est nécessaire doit les inclure.