Types entiers

CS-108

1. Introduction

Java comporte cinq types primitifs dits types entiers (integral types) : byte, short, int, long et char. Malgré leur nom, aucun ne correspond vraiment à la notion mathématique d'entier — l'ensemble \(\mathbb Z\). Il s'agit en réalité de vecteurs de bits interprétés comme des entiers, comme nous allons le voir.

2. Représentation des entiers

Les entiers Java sont des vecteurs de bits (pour binary digit) de taille fixe. Ainsi, une valeur de type byte est un vecteur de 8 bits, une valeur de type short ou char un vecteur de 16 bits, une valeur de type int un vecteur de 32 bits, et une valeur de type long un vecteur de 64 bits.

Ces vecteurs de bits sont ensuite interprétés comme des entiers. Deux interprétations coexistent en Java : l'interprétation non signée, dans laquelle tout vecteur de bits représente un entier positif ou nul, et l'interprétation signée en complément à deux, dans laquelle un vecteur de bits représente un entier négatif, nul ou positif.

2.1. Interprétation non signée

L'interprétation non signée (unsigned) consiste à interpréter un vecteur de bits comme un nombre exprimé en base 2. Dans ce cas, la valeur \(n\) de l'entier représenté par le vecteur de \(N\) bits \(b_{N-1}b_{N-2}\ldots b_{1}b_{0}\) est donnée par la formule suivante :

\[ n = \sum_{i=0}^{N-1} b_i\cdot 2^i \]

Par exemple, le vecteur de \(N=8\) bits 10001100 est interprété comme l'entier 140 :

\begin{align*} & 1\cdot 2^7 + 0\cdot 2^6 + 0\cdot 2^5 + 0\cdot 2^4 + 1\cdot 2^3 + 1\cdot 2^2 + 0\cdot 2^1 + 0\cdot 2^0\\ =\ & 2^7 + 2^3 + 2^2\\ =\ & 128 + 8 + 4\\ =\ & 140 \end{align*}

Dans un vecteur de bits interprété comme un entier, tous les bits n'ont pas la même importance :

le bit le plus à droite (\(b_0\)) vaut 1 s'il est à 1, 0 sinon,
le second bit depuis la droite (\(b_1\)) vaut 2 s'il est à 1, 0 sinon,
le troisième bit depuis la droite (\(b_2\)) vaut 4 s'il est à 1, 0 sinon,
etc.

De manière générale, le bit à la position n vaut 2ⁿ s'il est à 1, 0 sinon. Pour cette raison, le bit le plus à gauche est dit bit de poids (le plus) fort (most-significant bit, ou MSB) tandis que le bit le plus à droite est dit bit de poids (le plus) faible (least-significant bit ou LSB).

L'interprétation non signée a l'inconvénient de ne pas permettre la représentation de valeurs négatives. Pour cette raison, elle n'est utilisée en Java que pour les valeurs de type char, qui sont toutes positives. Les valeurs des quatre autres types entiers sont quant à elles interprétées en complément à deux, comme décrit ci-après.

2.2. Interprétation signée en complément à deux

L'interprétation (signée) en complément à deux (two's complement) est similaire à l'interprétation non signée, la seule différence étant que le poids du bit de poids le plus fort a un signe négatif. Ainsi, dans cette interprétation, la valeur \(n\) de l'entier représenté par le vecteur de \(N\) bits \(b_{N-1}b_{N-2}\ldots b_{1}b_{0}\) est donnée par la formule suivante :

\[ n = -b_{N-1}\cdot 2^{N-1} + \sum_{i=0}^{N-2} b_i\cdot 2^i \]

Par exemple, le vecteur de \(N=8\) bits 10001100 présenté plus haut est interprété en complément à deux comme l'entier –116 :

\begin{align*} & -1\cdot 2^7 + 0\cdot 2^6 + 0\cdot 2^5 + 0\cdot 2^4 + 1\cdot 2^3 + 1\cdot 2^2 + 0\cdot 2^1 + 0\cdot 2^0\\ =\ & -(2^7) + 2^3 + 2^2\\ =\ & -128 + 8 + 4\\ =\ & -116 \end{align*}

Le complément à deux a plusieurs propriétés importantes :

le bit de poids fort donne le signe de la valeur : s'il vaut 0, elle est positive ou nulle, s'il vaut 1, elle est négative,
un vecteur de n bits peut représenter :
- 2^n-1 – 1 valeurs strictement positives,
- 2^n-1 valeurs strictement négatives, et
- zéro (qui n'a qu'une représentation).

Il est important de comprendre que la notion de signe n'est qu'une question d'interprétation. C'est-à-dire qu'un vecteur de bits donné peut être interprété soit comme une valeur non signée (c-à-d non négative), soit comme une valeur signée en complément à deux.

En Java, les valeurs de tous les types entiers sauf char sont interprétées comme des valeurs signées en complément à deux, tandis que les valeurs de type char sont interprétées comme non signées. Ainsi, un vecteur de 16 bits valant tous 1 est interprété comme l'entier -1 si on lui donne le type short, mais comme l'entier 65'535 (2¹⁶ – 1) si on lui donne le type char, comme l'illustre le programme ci-dessous :

short s = (short)0b11111111_11111111;
char c  = (char) 0b11111111_11111111;
System.out.println((int)s);     // affiche -1
System.out.println((int)c);     // affiche 65535

(La notation 0b11…11 utilisées aux deux premières lignes représente une constante entière donnée en base 2, et est décrite en détail à la section suivante.)

En résumé, les types short et char font tous les deux 16 bits, la seule différence entre les deux étant la manière dont ces bits sont interprétés.

3. Notation des entiers

En Java, les valeurs entières constantes — appelées aussi entiers littéraux (integer literals) — peuvent être écrites en quatre bases : 2 (binaire), 8 (octal), 10 (décimal) et 16 (hexadécimal).

Par défaut, les valeurs entières constantes sont en base 10, par exemple :

int earthRadius = 6371;

Les chiffres d'un entier littéral peuvent être séparés par des caractères souligné (_) pour faciliter la lecture :

int earthRadius = 6_371;

Les entiers littéraux ont toujours le type int, sauf si on leur ajoute le suffixe l ou L, auquel cas ils ont le type long :

long earthPopulation = 7_130_000_000L;

Aucun suffixe similaire n'existe pour byte ou short, il faut donc recourir à des conversions, implicites ou explicites.

Les entiers littéraux peuvent être écrits en binaire, il suffit pour cela de leur ajouter le préfixe 0b ou 0B :

int twelve = 0b1100; // vaut 12
int maxInt = 0b01111111_11111111_11111111_11111111;
long twelveAsLong = 0b1100L; // vaut 12

Attention, ces entiers littéraux binaires peuvent être négatifs même en l'absence de signe de négation (-) :

// vaut -1
int minusOne = 0b11111111_11111111_11111111_11111111;

et, dès lors, positifs même en présence d'une négation :

// vaut 1
int plusOne = -0b11111111_11111111_11111111_11111111;

Les entiers littéraux peuvent être écrits en hexadécimal (base seize) avec le préfixe 0x ou 0X. Les lettres A à F — minuscule ou majuscule — sont utilisées pour représenter les chiffres après 9 :

int twelve = 0xC;                       // vaut 12
int thirtyTwo = 0x20;                   // vaut 32
int x = 0xDEAD_BEEF;                    // vaut -559038737
long minusOne = 0xFFFF_FFFF_FFFF_FFFFL; // vaut -1 (long)

L'intérêt de la notation hexadécimale par rapport à la notation décimale est que chaque chiffre représente exactement quatre bits.

Finalement, les entiers littéraux peuvent être écrits en octal (base huit) grâce au préfixe 0. Cette notation, héritée du langage C, est totalement anachronique mais il faut néanmoins la connaître car elle peut engendrer des surprises étant donné le préfixe utilisé ! En effet, mettre un (ou plusieurs) 0 en tête d'un entier littéral change sa base, donc généralement sa valeur. Par exemple :

int thirty    =  30; // vaut 30
int notThirty = 030; // vaut 24 (!)

4. Opérations arithmétiques

Les opérations arithmétiques de base sont disponibles sur les entiers, à savoir :

l'addition : x + y,
la soustraction : x - y,
la multiplication : x * y,
la division entière : x / y,
le reste de la division entière, souvent appelé modulo : x % y.

La plupart de ces opérations peuvent produire des valeurs non représentables dans le type entier concerné. On dit alors qu'il y a dépassement de capacité (overflow).

En cas de dépassement de capacité, la valeur résultant de l'opération arithmétique est simplement tronquée au nombre de bits du type du résultat. Dès lors, cette valeur est incorrecte d'un point de vue mathématique. En particulier, notez qu'en raison de l'utilisation du complément à deux, il est même possible que le résultat n'ait pas le bon signe !

Les dépassements de capacité sont la source de nombreux problèmes de sécurité, particulièrement dans des langages non sûrs comme C et C++.

Le comportement en cas de dépassement de capacité peut s'illustrer en calculant la somme de 120 (01111000 en binaire) et 10 (00001010) sur des entiers de type byte (8 bits) :

bit	7	6	5	4	3	1
retenue	1	1	1	1	0	0
120	0	1	1	1	1	0
10	0	0	0	0	1	1
somme	1	0	0	0	0	1

En d'autres termes, si on calcule la somme 120 + 10 avec des valeurs de type byte, on obtient –126 (10000010) et pas 130 ! Le même genre de problèmes existe avec les autres types entiers, mais pour des valeurs plus grandes.

Parmi les problèmes moins évidents dus aux dépassement de capacité, on peut en citer deux :

la valeur absolue d'un entier Java peut être négative — si cet entier est la plus petite valeur entière représentable, p.ex. 0x80000000 pour le type int,
la négation (-) peut se comporter en Java comme l'identité pour une valeur non nulle — là aussi, cela n'est vrai que pour la plus petite valeur entière représentable.

Il est bon de garder cela à l'esprit, surtout lorsqu'on écrit du code sensible.

5. Opérations bit à bit

En plus des opérations arithmétiques, Java offre ce que l'on appelle des opérations bit à bit (bitwise operations) sur les types entiers.

Ces opérations adoptent un point de vue différent des entiers que les opérations arithmétiques, puisqu'elles les considèrent comme les vecteurs de bits qu'ils sont réellement, et pas comme les entiers qu'ils représentent.

Dès lors, initialement en tout cas, il est préférable de ne pas mélanger ces deux points de vue, et de traiter les entiers Java soit comme des entiers mathématiques — auxquels on applique des opérations arithmétiques — soit comme des vecteurs de bits — auxquels on applique des opérations bit à bit.

En Java, les opérations bit à bit sont au nombre de sept :

l'inversion (ou complément) : ~x,
la conjonction (et) bit à bit : x & y,
la disjonction (ou) bit à bit : x | y,
la disjonction exclusive (ou exclusif) bit à bit : x ^ y,
le décalage à gauche : x << y,
le décalage à droite arithmétique : x >> y,
le décalage à droite logique : x >>> y.

5.1. Inversion

L'inversion ou complément parallèle ou bit à bit (bitwise complement), noté ~, inverse chaque bit de son opérande.

Par exemple, ~0b11110000 vaut 0b00001111.

Etant donné que les valeurs négatives sont représentées au moyen du complément à deux, l'inversion et la négation sont liées par l'égalité suivante, valable pour toute valeur x d'un type entier, char excepté :

-x == ~x + 1

5.2. Opérateurs parallèles

Les opérateurs binaires parallèles ou bit à bit (binary bitwise operators) &, | et ^ appliquent la même opération à chacun des bits de leurs opérandes. Ces opérations sont définies par les tables ci-dessous.

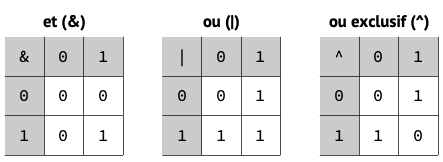
bitwise-tables;16.png — Figure 1 : Tables de vérité des opérateurs bit à bit

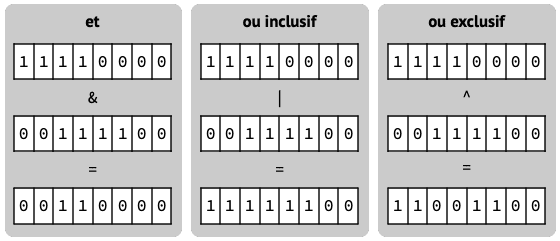
Par exemple, appliquées aux opérandes 11110000 et 00111100, ces trois opérations produisent les résultats illustrés dans la figure suivante.

bitwise-example;16.png — Figure 2 : Exemple des opérateurs bit à bit

5.3. Décalages

La valeur de l'expression x << y est obtenue par décalage vers la gauche, de y positions, des bits de x.

Par exemple, 0b00001100 << 3 vaut 0b01100000, car tous les bits de la première opérande sont décalés de 3 positions sur la gauche, les trois de poids fort sont perdus, et trois bits nuls sont insérés à droite. Cela est illustré sur la figure ci-dessous.

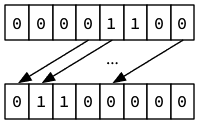
left-shift;16.png — Figure 3 : Décalage à gauche de 3 positions

Attention : seuls les 5 (respectivement 6) bits de poids faible de la seconde opérande sont pris en compte pour déterminer l'amplitude du décalage lors du décalage d'une valeur de type int (respectivement long).

Les deux opérateurs de décalage à droite, >> et >>>, sont similaires à celui de décalage à gauche, mais travaillent dans la direction opposée.

Le décalage dit arithmétique, noté >>, copie le bit de poids fort dans toutes les positions laissées libres par le décalage. Le décalage dit logique, noté >>>, insère quant à lui des bits nuls, comme l'opérateur de décalage à gauche.

Les deux opérateurs de décalage à droite ne diffèrent que pour les valeurs dont le bit de poids fort vaut 1, c-à-d les valeurs représentant des entiers négatifs. Pour de telles valeurs, le décalage arithmétique préserve le signe et produit donc une valeur négative, tandis que le décalage logique produit une valeur positive pour tout décalage d'amplitude non nulle.

5.4. Décalages et multiplications

Un décalage à gauche de n bits est équivalent à une multiplication par 2ⁿ, pour la même raison que, en base 10, un décalage à gauche de n positions des chiffres d'un nombre est équivalent à une multiplication par 10ⁿ :

x << n == x * pow(2, n)

où pow(2, n) représente 2ⁿ.

Un décalage à droite de n bits est équivalent à une division entière par 2ⁿ, pour les valeurs non négatives seulement :

x >> n == x / pow(2, n)         // (si x ≥ 0)

Pour les valeurs négatives, les deux expressions diffèrent d'une unité dans certains cas.

5.5. Schémas d'utilisation

Certaines constructions impliquant les opérateurs bit à bit sont fréquemment utiles, et il est donc bon de les connaître. Les plus importantes d'entre elles sont présentées ci-après.

5.5.1. Masques

Il est souvent utile de manipuler un ou plusieurs bits d'un entier sans toucher aux autres. Pour ce faire, on construit tout d'abord un entier — appelé le masque (mask) — dont seuls les bits à manipuler sont à 1. Ensuite, on utilise l'opération bit à bit appropriée (&, | ou ^), appliquée au masque et à la valeur.

Un masque peut soit s'écrire directement sous forme d'entier littéral — généralement en base 2 ou 16 — soit se construire en combinant décalages et disjonctions :

int mask13 = 1 << 13;            // uniquement bit 13
int mask17 = 1 << 17;            // uniquement bit 17
int mask13_17 = mask13 | mask17; // bits 13 et 17

Un masque composé d'une longue séquence de bits à 1 peut s'obtenir en combinant judicieusement un décalage et une soustraction. Par exemple, pour obtenir un masque dont les n bits de poids faible sont à 1, on peut écrire :

int mask = (1 << n) - 1;

5.5.2. Test de bit(s)

Pour tester si un ou plusieurs bits d'un entier sont à 1, on utilise le « et bit à bit » (&) entre le masque et l'entier, puis on regarde si la valeur obtenue est égale au masque.

Par exemple, pour tester si les bits 13 et 17 de l'entier x sont à 1, on écrit :

boolean bits13_17Set = (x & mask13_17) == mask13_17;

Pour tester si tous ces bits sont à 0, on écrit :

boolean bits13_17Cleared = (x & mask13_17) == 0;

Pour tester si au moins l'un de ces bits est à 1, on écrit :

boolean bit13OrBit17Set = (x & mask13_17) != 0;

5.5.3. (Dés)activation de bits

Pour activer (c-à-d mettre à 1) un ou plusieurs bits d'un entier sans toucher aux autres, on utilise le « ou bit à bit » (|) appliqué au masque et à l'entier.

Par exemple, pour mettre à 1 les bits 13 et 17 de l'entier x, on écrit :

int xWithBits13_17Set = x | mask13_17;

Pour désactiver (c-à-d mettre à 0) un ou plusieurs bits d'un entier sans toucher aux autres, on utilise le « et bit à bit » (&) appliqué au complément du masque et à l'entier.

Par exemple, pour mettre à 0 les bits 13 et 17 de l'entier x, on écrit :

int xWithBits13_17Cleared = x & ~mask13_17;

Pour inverser un ou plusieurs bits d'un entier sans toucher aux autres, on utilise le « ou exclusif bit à bit » appliqué au masque et à l'entier.

Par exemple, pour inverser les bits 13 et 17 de l'entier x, on écrit :

int xWithBits13_17Toggled = x ^ mask13_17;

5.5.4. Multiplication et division par une puissance de deux

La multiplication par une puissance de deux peut se faire au moyen d'un décalage à gauche :

x * pow(2, n) == x << n

Pour les valeurs non négatives uniquement, la division par une puissance de deux peut se faire au moyen d'un décalage à droite :

x / pow(2, n) == x >> n         // (si x ≥ 0)

Pour ces mêmes valeurs, le reste de la division par une puissance de deux peut se faire par masquage :

x % pow(2, n) == x & ((1 << n) - 1) // (si x ≥ 0)

Un cas particulier du reste d'une division par une puissance de deux est le test de parité : pour savoir si une valeur est paire (respectivement impaire), il suffit de regarder si son bit de poids faible vaut 0 (respectivement 1). Cela fonctionne également pour les valeurs négatives.

Par exemple, pour tester si l'entier x est pair, on écrit :

boolean isXEven = (x & 1) == 0;

et pour tester s'il est impair :

boolean isXOdd = (x & 1) == 1;

6. Entiers dans l'API Java

La bibliothèque Java contient, dans le paquetage java.lang, une classe pour chaque type d'entier :

Byte pour byte,
Short pour short,
Integer pour int,
Long pour long,
Character pour char.

Ces classes ont deux buts :

servir de « classes d'emballage » pour la généricité,
offrir, sous forme de méthodes généralement statiques, des opérations sur les valeurs du type qu'elles représentent.

La première utilisation est décrite dans le cours sur la généricité, nous nous concentrerons donc ici sur la seconde en examinant quelques attributs et méthodes de ces classes.

6.1. Taille des types

Chaque classe d'entiers fournit des attributs statiques donnant des informations quant à la taille du type entier correspondant :

MIN_VALUE et MAX_VALUE donnent respectivement la plus petite et la plus grande valeur représentable par le type entier,
SIZE donne la taille, en bits, du type entier,
BYTES donne la taille, en octets (groupe de 8 bits), du type entier.

Les attributs SIZE et BYTES dépendent bien entendu l'un de l'autre, SIZE valant toujours huit fois BYTES.

Par exemple, Byte.MIN_VALUE vaut –128, Byte.MAX_VALUE vaut 127, Byte.SIZE vaut 8 et Byte.BYTES vaut 1.

6.2. Conversions de/vers texte

Les classes Integer et Long offrent deux variantes d'une méthode statique permettant de convertir un entier en chaîne de caractères. Par exemple, Integer offre :

String toString(int i, int b) : retourne la chaîne représentant l'entier i en base b (où 2 ≤ b ≤ 36),
String toString(int i) : idem pour la base 10.

Les classes Byte et Short offrent uniquement la seconde variante.

Chaque classe d'entiers offre deux variantes d'une méthode statique permettant de transformer une chaîne en l'entier signé correspondant. Par exemple, Integer offre :

int parseInt(String s, int b) : retourne l'entier dont la représentation en base b (où 2 ≤ b ≤ 36) est la chaîne s, ou lève une exception si la chaîne est invalide ;
int parseInt(String s) : idem pour la base 10.

Les classes Byte, Short et Long offrent des méthodes similaires, nommées respectivement parseByte, parseShort et parseLong.

6.3. Comptage de bits

Integer et Long offrent des méthodes statiques permettant de compter certains types de bits. Par exemple, Integer offre :

int bitCount(int i) : retourne le nombre de bits à 1 dans i ;
int numberOfLeadingZeros(int i) : retourne le nombre de bits à 0 en tête (à gauche) de i ;
int numberOfTrailingZeros(int i) : retourne le nombre de bits à 0 en queue (à droite) de i.

Les méthodes de Long sont identiques mais prennent un argument de type long.

6.4. Position des bits

Integer et Long offrent des méthodes statiques permettant de déterminer la position de certains bits. Par exemple, Integer offre :

int lowestOneBit(int i) : retourne 0 si i vaut 0, ou une valeur ayant un seul bit à 1, dont la position est celle du bit à 1 de poids de plus faible de i,
int highestOneBit(int i) : idem, mais pour le bit de poids le plus fort.

Ainsi :

Integer. lowestOneBit(0b1110) == 0b0010
Integer.highestOneBit(0b1110) == 0b1000

6.5. Rotation

Les classes Integer et Long offrent chacune des méthodes statique permettant d'effectuer une rotation des bits. Par exemple, Integer offre :

int rotateLeft(int i, int d) : retourne l'entier obtenu par rotation des bits de i de d positions vers la gauche ;
int rotateRight(int i, int d) : idem, mais vers la droite.

Une rotation est similaire à un décalage, mais les bits qui sont éjectés d'un côté sont réinjectés de l'autre.

6.6. Inversion de bits et octets

Les classes Integer et Long offrent des méthodes statiques permettant d'inverser l'ordre des bits ou des octets d'un entier. Par exemple, Integer offre :

int reverse(int i) : retourne l'entier obtenu en inversant l'ordre des bits de i ;
int reverseBytes(int i) : retourne l'entier obtenu en inversant l'ordre des octets de i.

Short offre également reverseBytes.

7. Empaquetage

Etant donné que les entiers sont en réalité des vecteurs de bits, il est assez fréquent de les utiliser pour contenir plusieurs petites valeurs. On dit alors que ces valeurs sont empaquetées (packed) dans un entier.

Par exemple, un entier de type int faisant 32 bits, on peut y stocker 32 valeurs binaires, ou 4 valeurs de 8 bits, etc. Cette technique est souvent utilisée pour représenter les couleurs, exemple qu'il vaut la peine d'examiner en détail.

7.1. Couleurs empaquetées

En informatique, une couleur est souvent représentée par ses trois composantes rouge, verte et bleue, chacune étant — conceptuellement — un nombre réel compris entre 0 et 1 (inclus).

La manière la plus naturelle de représenter une telle couleur en Java consiste à créer une classe dotée de trois champs de type double (ou float). Bien que naturelle, cette représentation est coûteuse en espace : sachant qu'une valeur de type double fait 8 octets (64 bits), chaque couleur nécessite au moins 3×8 = 24 octets (192 bits), ou la moitié si le type float est utilisé.

Une manière plus compacte, mais moins précise, de représenter une couleur consiste à représenter chacune de ses composantes par un entier de 8 bits — compris entre 0 et 255 — puis à les empaqueter dans un entier de 32 bits. Les 8 bits restants sont soit inutilisés, soit utilisés pour stocker l'opacité de la couleur. De la sorte, une couleur occupe exactement 32 bits au lieu de 192 dans la représentation précédente, un gain appréciable.

Les composantes d'une couleur peuvent être empaquetées de nombreuses manières. Dans ce qui suit, la composante bleue est placée dans les huit bits de poids faible, suivie de la verte puis la rouge. Cette technique d'empaquetage est souvent désignée par l'acronyme RGB.

bits	31 … 24	23 … 16	15 … 8	7 … 0
contenu	inutilisés	rouge (R)	vert (G)	bleu (B)

La notation hexadécimale convient assez bien pour écrire directement des couleurs empaquetées de la sorte, car chaque composante occupe exactement deux chiffres hexadécimaux (8 bits). Par exemple 0xFF_00_00 représente un rouge pur (1,0,0).

Le passage d'une couleur exprimée sous la forme de trois composantes réelles comprises entre 0 et 1 à une couleur empaquetée RGB se fait en combinant décalages et « ou » parallèle :

double r = …, g = …, b = …;
int r0 = (int)(r * 255.9999); // 0 ≤ r0 ≤ 255
int g0 = (int)(g * 255.9999); // 0 ≤ g0 ≤ 255
int b0 = (int)(b * 255.9999); // 0 ≤ b0 ≤ 255
int rgb = (r0 << 16) | (g0 << 8) | b0;

Une composante quelconque d'une couleur empaquetée peut être extraite en combinant un décalage avec un masquage. Par exemple, la composante verte peut être obtenue par un décalage à droite de 8 bits suivi d'un masquage pour ne garder que les 8 bits de poids faible :

int rgb = …;
int g0 = (rgb >> 8) & 0xFF;

Cette valeur entière, comprise entre 0 et 255, peut être ramenée à l'intervalle [0;1] par une simple division :

double g = (double)g0 / 255d;

8. Références

la documentation de l'API Java, en particulier les classes et interfaces suivantes :
- la classe Byte,
- la classe Short,
- la classe Integer,
- la classe Long,
- la classe Character,
The Java® Language Specification, de James Gosling et coauteurs, en particulier :
Hacker's delight de Henry Warren,
Matters computational de Jörg Arndt, en particulier le chapitre 1, Bit wizardry.