Généricité avancée
CS-108
1. Introduction
Les bases de la généricité en Java ont été introduites lors d'une leçon précédente. Il reste néanmoins deux aspects de la généricité à présenter : les bornes inférieures et les jokers. Avant de pouvoir les présenter, il importe toutefois d'examiner en détail la notion de sous-typage, cruciale à leur compréhension.
2. Sous-typage
En Java, chaque classe, énumération et interface définit un type, et ces types sont liés entre eux par une relation de sous-typage. Cette relation de sous-typage est déterminée par la manière dont les classes et interfaces sont liées entre elles : lorsqu'une classe hérite d'une autre, son type est sous-type de celui de sa super-classe, et il en va de même pour les interfaces ; de plus, lorsqu'une classe implémente une interface, son type est sous-type de celui de l'interface.
Par exemple, le type String est un sous-type du type Object car la classe String hérite de la classe Object. De manière similaire, le type Number est un sous-type du type Serializable car la classe Number implémente l'interface Serializable.
Pour mémoire, le sous-typage est important en raison du polymorphisme d'inclusion, qui permet de substituer à une valeur d'un type T1 donné une valeur d'un autre type T2 pour peu que T2 soit un sous-type de T1. On appelle aussi cela le principe de substitution (substitution principle).
Par exemple, si une fonction prend en argument une valeur de type Number, en plus d'une valeur de ce type on peut lui passer une valeur de type Integer, Double, etc. qui sont des sous-types de Number. Ainsi, l'appel à add ci-dessous est valide en raison du principe de substitution :
Number add(Number n1, Number n2) {
return new Double(n1.doubleValue() + n2.doubleValue());
}
add(new Integer(1), new Double(3.14));
Formellement, la relation de sous-typage est :
- réflexive, c-à-d que tout type est sous-type de lui-même,
- transitive, c-à-d que si un type T1 est sous-type d'un type T2 et T2 est sous-type de T3, alors T1 est aussi sous-type de T3,
- anti-symétrique, c-à-d que si T1 est sous-type de T2 et T2 est sous-type de T1, alors T1 = T2.
En mathématiques, une relation possédant ces trois propriétés est appelée un ordre partiel (partial order).
Comme tout ordre partiel, la relation de sous-typage Java peut être visualisée sous la forme d'un graphe dirigé dans lequel chaque type est un nœud et un arc lie le nœud d'un type à celui de ses super-types directs. La figure 1 présente un minuscule extrait du graphe des types standard Java.
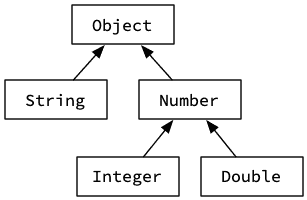
A noter que lorsqu'un type T2 est sous-type d'un type T1, on dit que T1 est un super-type de T2.
3. Sous-typage et généricité
Le sous-typage et la généricité interagissent de manière non triviale et parfois surprenante. Pour l'illustrer, nous utiliserons l'interface générique List ci-dessous, une version simplifiée de celle de la bibliothèque Java, ainsi que sa mise en œuvre (simplifiée) LinkedList, que l'on suppose exister.
public interface List<E> implements Iterable<E> {
void add(E newElem);
Iterator<E> iterator();
}
Le principe de substitution nous permet d'ajouter n'importe quel type de nombre — c-à-d n'importe quel sous-type de Number — à une liste de nombres :
List<Number> l = new LinkedList<>(); Integer i = 1; l.add(i); // valide car Integer est sous-type de Number Double d = 3.14; l.add(d); // valide car Double est sous-type de Number
Pour faciliter l'ajout de tous les éléments d'une liste à une liste existante, on peut vouloir ajouter une méthode addAll à List. Une première version de cette méthode pourrait ressembler à ceci :
public interface List<E> {
// …
void addAll(List<E> other);
}
public class LinkedList<E> implements List<E> {
// …
void addAll(List<E> other) {
for (E elem: other)
add(elem);
}
}
Malheureusement, cette méthode addAll n'est pas utilisable comme nous le désirerions, car l'ajout d'une liste d'entiers Integer à une liste de nombres Number est invalide :
List<Number> l = new LinkedList<>(); List<Integer> li = new LinkedList<>(); Integer i = 1; li.add(i); l.addAll(li); // refusé !
Ce code est refusé car, en Java, une instanciation d'un type générique n'est jamais sous-type d'une autre instanciation de ce même type générique ! Par exemple, le type List<U> n'est jamais sous-type de List<V> sauf dans le cas trivial où U = V. Nous verrons plus loin la raison de cette restriction.
Le seul moyen de rendre l'appel à addAll valide est donc de changer le type de la seconde liste pour en faire une liste de Number. Cela n'est pas très satisfaisant, car il est clairement valide d'ajouter une liste d'entiers à une liste de nombres. Il nous faudra trouver une solution !
Attention toutefois, la restriction mentionnée ne signifie pas que deux types génériques différents ne peuvent pas être liés par la relation de sous-typage. Par exemple, LinkedList<String> est un sous-type de List<String> car la classe générique LinkedList<E> implémente l'interface List<E>. Par contre, deux instanciations différentes du même type générique ne sont jamais liées entre elles par la relation de sous-typage.
Cela est illustré par la figure 2 qui montre la relation de sous-typage pour deux instanciations de List. Il est très important de noter l'absence de flèche (donc de relation de sous-typage) entre les deux instanciations de List ou de LinkedList.
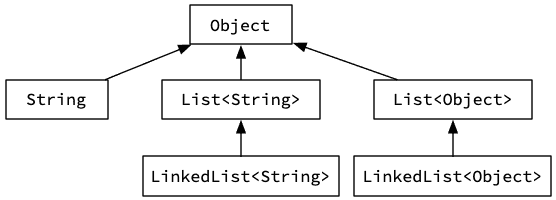
List
Pourquoi les concepteurs de la généricité Java ont-ils choisi d'imposer cette restriction ? Pour le comprendre, admettons que List<Integer> soit un sous-type de List<Number>. Cela nous autoriserait à écrire le code suivant :
void addPi(List<Number> l) {
l.add(3.14);
}
List<Integer> l = new LinkedList<>();
addPi(l);
Or ce code est clairement faux, car il ajoute un nombre réel — une valeur de type Double, pour être précis — à une liste de nombre entiers.
3.1. Borne supérieure
N'est-il pas possible de définir une méthode addAll qui soit plus générale que celle définie précédemment, et qui permette l'ajout — valide — d'une liste d'entiers à une liste de nombres ? Oui, mais il faut pour cela la rendre générique et borner son paramètre de type. C'est ce qui est fait dans la nouvelle version de la méthode addAll ci-dessous :
interface List<E> {
// …
<F extends E> void addAll(List<F> other);
}
Comme nous l'avons vu précédemment, la notation <F extends E> déclare que la méthode addAll est générique, son paramètre de type s'appelle F, et il est borné par E. Cela signifie que, pour qu'une utilisation de cette méthode soit valide, il faut que le type du paramètre F soit un sous-type du type du paramètre E.
Grâce à cette borne, le code précédent est maintenant valide :
List<Number> l = new LinkedList<>(); List<Integer> li = new LinkedList<>(); Integer i = 1; li.add(i); l.addAll(li);
et le type inféré pour le paramètre de type F est Integer. La borne est clairement respectée, puisque E est instancié à Number pour la liste l, et Integer est un sous-type de Number. En résumé, la borne (supérieure) utilisée ici permet l'utilisation de n'importe quel sous-type de la borne, Number dans cet exemple. Cela est illustré par la figure 3.
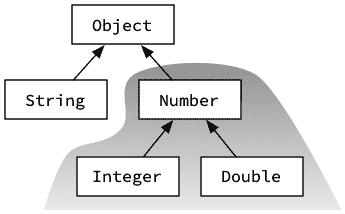
Bien entendu, changer le type dans l'interface List n'a de sens que si les mises en œuvre concrètes de la méthode restent valides. Pour addAll, c'est le cas :
public class LinkedList<E> implements List<E> {
// …
<F extends E> void addAll(List<F> other) {
for (F elem: other)
add(elem);
}
}
Cette définition de addAll est valide, car le principe de substitution autorise l'ajout, via la méthode add, d'un élément de type F à une liste dont les éléments ont le type E, étant donné que la borne garantit que F est un sous-type de E.
4. Jokers (ou wildcards)
Le paramètre de type F de la méthode addAll n'est pas utilisé ailleurs que dans son type. Il n'est donc pas nécessaire de le nommer, et Java permet d'utiliser dans ce cas un joker (wildcard) borné, noté ? :
public interface List<E> {
// …
void addAll(List<? extends E> other);
}
Cette version de addAll est totalement équivalente à la précédente, mais plus concise et donc généralement préférable.
A noter qu'il est aussi possible d'utiliser un joker sans le borner explicitement, ce qui équivaut à le borner avec Object. Par exemple, List<?> est équivalent à List<? extends Object>.
4.1. Bornes inférieures
Nous avons réussi à définir une méthode addAll satisfaisante. Essayons maintenant de définir une méthode addAllInto qui ajoute tous les éléments du récepteur dans la liste passée en argument. Notre première tentative pourrait ressembler à ceci :
public interface List<E> {
// …
void addAllInto(List<E> other);
}
class LinkedList<E> implements List<E> {
// …
void addAllInto(List<E> other) {
other.addAll(this);
}
}
Bien entendu, cette première version possède les mêmes limitations que notre première version de la méthode addAll, à savoir que le code suivant est invalide :
List<Number> l = new LinkedList<>(); List<Integer> li = new LinkedList<>(); Integer i = 1; li.add(i); li.addAllInto(l); // refusé !
Nous pourrions bien entendu essayer de résoudre le problème de la même manière que pour addAll, c-à-d en utilisant un joker équipé d'une borne supérieure :
public interface List<E> {
// …
void addAllInto(List<? extends E> other);
}
List<Number> l = new LinkedList<>();
List<Integer> li = new LinkedList<>();
Integer i = 1;
li.add(i);
li.addAllInto(l);
Malheureusement cela ne fonctionne pas car la borne de addAllInto doit être une borne inférieure et pas supérieure ! Heureusement, Java offre de telles bornes sur les jokers — mais pas sur les paramètres de type :
public interface List<E> {
// …
void addAllInto(List<? super E> other);
}
List<Number> l = new LinkedList<>();
List<Integer> li = new LinkedList<>();
Integer i = 1;
li.add(i);
li.addAllInto(l);
La borne inférieure permet l'utilisation de n'importe quel super-type de la borne, ici Integer, ce qui est illustré par la figure 4.
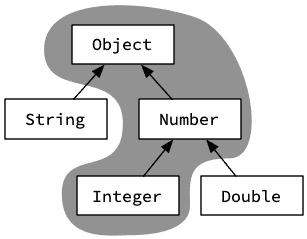
Pour terminer, admettons que l'on désire définir une méthode addAllFromAndInto qui ajoute tous les éléments de l'argument au récepteur et inversement :
public interface List<E> {
// …
void addAllFromAndInto(List<E> other);
}
class LinkedList<E> implements List<E> {
// …
void addAllFromAndInto(List<E> other) {
this.addAll(other);
other.addAll(this);
}
}
Quel type de borne utiliser et pourquoi ? Aucune — ou les deux, ce qui revient au même — car on veut à la fois lire et écrire dans le récepteur !
Règle des bornes :
Lorsqu'on désire uniquement lire dans une structure, on utilise une borne supérieure (avec extends) ; lorsqu'on désire uniquement y écrire, on utilise une borne inférieure (avec super) ; lorsqu'on désire à la fois y lire et y écrire, on n'utilise aucune borne.
En anglais, cette règle est parfois désignée par PECS, acronyme de Producer Extends, Consumer Super qui permet de se souvenir facilement que :
- lorsque la structure que l'on utilise est un producteur, c-à-d qu'on y lit des valeurs, il faut utiliser
extendspour borner son type, et - lorsque la structure que l'on utilise est un consommateur, c-à-d qu'on y écrit des valeurs, il faut utiliser
superpour borner son type.
Lorsqu'on désire à la fois lire et écrire, on ne peut borner son type.
5. Références
- Effective Java (3rd ed.) de Joshua Bloch, en particulier :
- la règle 31, Use bounded wildcards to increase API flexibility sur l'utilisation judicieuse des jokers bornés,
- Java Generics and Collections de Maurice Naftalin et Philip Wadler, O'Reilly Media,
- Java Generics FAQ d'Angelika Langer, une liste des questions fréquentes liées à la généricité Java, et leur réponse.