Nœuds et arêtes
JaVelo – étape 3
1. Introduction
Le but de cette troisième étape est d'écrire les classes représentant les nœuds et arêtes du graphe du réseau routier, dans lequel la recherche d'itinéraire se fera.
2. Concepts
2.1. Graphe
Un graphe (graph) est une structure mathématique composée de nœuds (nodes) reliés entre eux par des arêtes (edges). Les nœuds et les arêtes peuvent être annotés, ce qui signifie que certaines informations leur sont attachées.
Les graphes sont fréquemment utilisés en informatique, car de nombreux problèmes peuvent être exprimés sous cette forme et résolus au moyen d'algorithmes connus. La planification d'itinéraire en fait partie.
La figure ci-dessous montre un exemple de graphe dont les nœuds — représentés par des disques blancs — sont des villes de Suisse. Les arêtes — représentées par des flèches — relient les villes entre lesquelles il est possible de se déplacer, et sont annotées avec la longueur du trajet, en kilomètres.
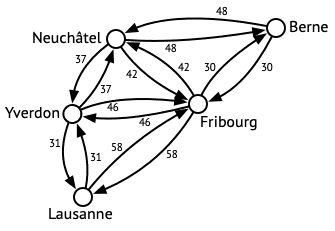
Pour planifier les itinéraires dans JaVelo, nous utiliserons un graphe similaire à celui ci-dessus, mais sensiblement plus détaillé.
2.2. Graphe JaVelo
Le graphe utilisé par JaVelo pour représenter le réseau routier est construit à partir des données OpenStreetMap. Ses nœuds correspondent donc directement aux nœuds OSM, tandis que ses arêtes sont des morceaux de voies OSM reliant ces nœuds entre eux.
La correspondance entre les données OSM et le graphe JaVelo est illustrée au moyen d'un exemple dans la figure 2 ci-dessous. La partie gauche de cette figure montre trois nœuds OSM d'identité 732, 182 et 912, reliés, dans cet ordre, par une unique voie dont l'identité est 12. La partie droite de cette figure montre le graphe JaVelo correspondant. Il contient également trois nœuds, qui correspondent directment aux nœuds OSM, mais dont les identités (2, 3, 5) sont propres à JaVelo. Ces nœuds sont reliés par quatre arêtes d'identités 4, 5, 6 et 7 : une pour chaque sens et pour chaque portion de la voie OSM.
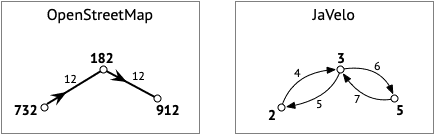
Les attributs attachés aux arêtes JaVelo sont un sous-ensemble des attributs attachés à la voie OSM correspondante. Pour ne pas alourdir l'image ci-dessus, ils n'y figurent pas. Dans un soucis de simplicité, aucun attribut n'est attaché aux nœuds JaVelo.
2.2.1. Identification des éléments du graphe
Comme l'exemple ci-dessus l'illustre, les nœuds et arêtes du graphe JaVelo sont identifiés par des entiers positifs. Ces identités ne sont toutefois pas celles d'OpenStreetMap, mais bien des identités propres à JaVelo.
L'identité d'un nœud JaVelo n'est rien d'autre que son index dans un grand tableau contenant la totalité des nœuds du graphe. Les nœuds y sont ordonnés de manière à ce que tous les nœuds se trouvant dans une zone géographique rectangulaire donnée se suivent.
Ces zones rectangulaires sont nommées des secteurs (sectors). Les secteurs ont été obtenus par découpage du rectangle de 349×221 km englobant la Suisse en 16 384 secteurs (128×128), qui font donc environ 2.73×1.73 km chacun.
L'intérêt de regrouper ainsi les nœuds en secteurs est qu'il est alors relativement simple de trouver tous les nœuds se trouvant dans une zone donnée. Cela nous sera fort utile lorsque nous devrons déterminer le nœud le plus proche de l'endroit où l'utilisateur a cliqué pour ajouter un point de passage.
Les secteurs sont numérotés de 0 à 16383, le secteur 0 étant dans le coin en bas à gauche du rectangle englobant la Suisse, le secteur 1 à sa droite, et ainsi de suite jusqu'au secteur 16383, qui se trouve dans le coin en haut à droite. Notez que de nombreux secteurs, p. ex. ceux des quatre coins, sont entièrement hors du territoire suisse. Ils ne contiennent donc aucun nœud, mais cela n'a pas d'importance.
L'identité d'une arête JaVelo correspond également à son index dans un tableau contenant la totalité des arêtes du graphe. Les arêtes y sont ordonnées de manière à ce que toutes les arêtes sortant d'un nœud donné se suivent. De la sorte, on peut obtenir la totalité des arêtes sortant d'un nœud donné en connaissant uniquement l'identité de la première d'entre elles, et leur nombre.
En plus des nœuds, des arêtes et des secteurs, les ensembles d'attributs et les échantillons des profils en long des arêtes sont également identifiés par leur position dans un grand tableau les contenant tous.
2.2.2. Nœuds
Un nœud JaVelo possède quatre attributs, donnés dans la table ci-dessous. La colonne Format spécifie la manière dont l'attribut est interprété. La notation Ux signifie qu'il s'agit d'un vecteur de x bits interprété de manière non signée (unsigned).
| Attribut | Bits | Format |
|---|---|---|
| Coordonnée E dans le système suisse | 32 | Q28.4 |
| Coordonnée N dans le système suisse | 32 | Q28.4 |
| Nombre d'arêtes sortantes | 4 | U4 |
| Identité (index) de la première arête sortante | 28 | U28 |
Ces quatre attributs sont représentés au moyen de 3 valeurs 32 bits. La première contient la coordonnée E, la seconde la coordonnée N, et la dernière contient à la fois le nombre d'arêtes sortantes du nœud et l'identité de la première d'entre elles : les 4 bits de poids fort, interprétés de manière non signée, donnent le nombre d'arêtes sortantes (entre 0 et 15, inclus) ; les 28 bits restants, interprétés de manière non signée, donnent l'identité de la première arête sortante.
Notez que l'identité (c.-à-d. l'index) d'un nœud n'est pas mentionnée comme attribut dans la table ci-dessus, car elle n'est pas stockée explicitement. Au lieu de cela, comme nous l'avons vu, les nœuds sont stockés dans un tableau, à l'index qui correspond à leur identité. Dès lors, on peut voir l'identité comme un attribut implicite d'un nœud, par opposition aux attributs explicites donnés dans la table.
2.2.3. Secteurs
Sachant que tous les nœuds appartenant à un secteur donné ont des identités consécutives, il suffit de connaître pour chaque secteur l'index du premier nœud qu'il contient, et leur nombre. Dès lors, un secteur JaVelo possède les deux attributs ci-dessous :
| Attribut | Bits | Format |
|---|---|---|
| Identité du premier nœud | 32 | U32 |
| Nombre de nœuds | 16 | U16 |
Tout comme les nœuds, les secteurs sont placés dans un tableau les contenant tous, à l'index qui correspond à leur identité.
2.2.4. Arêtes
Une arête JaVelo correspond, comme nous l'avons vu, à une portion d'une voie OSM. Il semble donc naturel qu'elle soit caractérisée au moins par son nœud de départ, son nœud d'arrivée, et le sous-ensemble de ses attributs OSM qui importent pour la recherche d'itinéraire.
Pour permettre à cette recherche d'itinéraire d'être efficace, il peut aussi être intéressant de calculer, au moment du pré-traitement des données OSM, certains attributs « dérivés », et de les attacher à l'arête. Par exemple, la longueur d'une arête pourrait se calculer au moyen des coordonnées de ses nœuds de départ et d'arrivée, mais il est plus efficace d'effectuer ce calcul une fois pour toutes et d'ajouter la longueur aux attributs de l'arête.
Les attributs d'une arête JaVelo sont donc composés d'attributs fondamentaux et d'attributs dérivés, résumés dans la table suivante :
| Attribut | Bits | Format |
|---|---|---|
| Sens de l'arête | 1 | |
| Identité du nœud destination | 31 | U31 |
| Longueur (en mètres) | 16 | UQ12.4 |
| Dénivelé positif (en mètres) | 16 | UQ12.4 |
| Identité de l'ensemble d'attributs OSM | 16 | U16 |
L'attribut sens de l'arête permet de savoir si l'arête JaVelo va dans le même sens que la voie OSM dont elle provient, ou dans le sens contraire. Cette information permet d'une part de correctement interpréter certains attributs OSM — comme oneway=yes attaché aux routes à sens unique — et d'autre part de correctement ordonner les échantillons des profils en long, comme nous le verrons plus bas.
Le sens de l'arête et l'identité (index) du nœud destination sont représentés par une seule valeur de 32 bits. Toutefois, cette valeur est construite de manière particulière et doit être interprétée ainsi :
- si elle est positive ou nulle, alors l'arête va dans le même sens que la voie OSM, et la valeur donne directement l'identité du nœud destination,
- si elle est négative, alors l'arête va dans le sens inverse de la voie OSM, et l'identité du nœud destination s'obtient par complément de la totalité des bits de la valeur de 32 bits.
Il faut noter que l'identité du nœud de départ de l'arête ne figure pas dans la table ci-dessus. Cela est dû au fait que, lorsqu'on accède à une arête lors de la recherche d'itinéraire, on connaît son nœud de départ, et il n'est donc pas nécessaire de stocker cette information.
En plus des attributs donnés dans la table plus haut, dérivés pour la plupart des données OSM, les arêtes JaVelo possèdent également un profil en long, dérivé du modèle SwissALTI3D. Ce profil est spécifié par les deux attributs suivants, qui s'ajoutent à ceux de la table précédente :
| Attribut | Bits | Format |
|---|---|---|
| Type de profil | 2 | U2 |
| Identité du premier échantillon du profil | 30 | U30 |
Ces deux attributs sont empaquetés dans une unique valeur de 32 bits : les 2 bits de poids fort, interprétés de manière non signée, contiennent le type du profil, décrit plus bas ; les 30 bits restants, interprétés également de manière non signée, contiennent l'identité (index) du premier échantillon du profil.
Les échantillons du profil sont toujours ordonnés dans le sens de la voie OSM. Dès lors, leur ordre doit être inversé pour les arêtes qui vont dans le sens contraire de la voie. Cette convention permet à deux arêtes joignant les mêmes nœuds mais de sens opposé de se partager un seul ensemble d'échantillons.
Il existe quatre types de profils différents, résumés dans la table suivante :
| Type | Signification |
|---|---|
| 0 | Profil inexistant |
| 1 | Profil non compressé |
| 2 | Profil compressé au format Q4.4 |
| 3 | Profil compressé au format Q0.4 |
Le type 0 est celui des arêtes sans profil. Ces arêtes correspondent soit à des ponts, soit à des tunnels, et leur profil ne peut pas être déterminé car le modèle SwissALTI3D donne l'altitude à la surface de la Terre, or ni les tunnels ni les ponts ne s'y trouvent.
Les trois autres types de profils sont décrits ci-après.
2.2.5. Profils
Le profil en long d'une arête est une fonction échantillonnée donnant l'altitude en fonction de la distance le long de l'arête. Le nombre d'échantillons du profil d'une arête est déterminé par la longueur \(l\) de cette arête (en mètres), au moyen de la formule suivante :
\[ 1 + \left\lceil\frac{l}{2}\right\rceil \]
qui garantit que la distance séparant deux échantillons est de 2 m au maximum.
Théoriquement, les profils pourraient être stockés sous la forme d'une séquence d'échantillons, et ces séquences pourraient être placées bout à bout dans un grand tableau, au même titre que les nœuds ou les arêtes. C'est d'ailleurs comme cela que les profils non compressés (type 1) sont représentés, chaque échantillon étant constitué de 16 bits au format UQ12.4.
Cela dit, la plupart des profils peut être stockée de manière compressée, ce qui permet d'économiser de la mémoire. Les profils compressés sont représentés ainsi :
- le premier échantillon est représenté par une valeur de 16 bits, au format UQ12.4, comme dans la représentation non compressée,
- les échantillons suivants sont représentés par la différence d'altitude par rapport à leur prédécesseur, représentée soit par une valeur de 8 bits au format Q4.4 (type 2), soit par une valeur de 4 bits au format Q0.4 (type 3).
Les différences sont ensuite empaquetées dans des valeurs de 16 bits, contenant chacune 2 (type 2) ou 4 (type 3) différences.
La table ci-dessous montre les différences d'altitudes (δ) et les pentes (↘ et ↗) minimales et maximales que chacune des deux représentation compressée permet de représenter :
| Type | Bits | δ min | δ max | ↘ max | ↗ max |
|---|---|---|---|---|---|
| 2 | 8 | -8 | 7.9375 | 400.0% | 396.9% |
| 3 | 4 | -0.5 | 0.4375 | 25.0% | 21.9% |
Sachant qu'aucune route au monde n'a de pente supérieure ou égale à 400%, il peut sembler étrange que la représentation compressée de type 2 ne suffise pas dans toutes les circonstances. C'est malheureusement le cas, pour deux raisons : d'une part, certaines arêtes JaVelo représentent des escaliers ou des chemins de montagne, qui peuvent être très raides ; et d'autre part, les données OSM et le modèle SwissALTI3D ne sont pas toujours parfaitement alignés, ce qui peut donner lieu à des pentes extrêmes, bien qu'erronées.
2.2.6. Exemple de profil
Pour illustrer la représentation compressée des profils, voyons comment celui d'une partie de la piste cyclable passant devant le centre sportif UNIL-EPFL peut être représenté. Cette piste cyclable est représentée par plusieurs voies OSM, dont celle d'identité 69929283. Les deux premiers nœuds de cette voie ont les identités OSM 835836139 et 835836216.
L'existence de cette voie OSM implique entre autres l'existence d'une arête dans le graphe JaVelo allant du premier de ces deux nœuds au second. La longueur de cette arête, arrondie au 1/16e de mètre, est de 16.6875 m. Il en découle que son profil contient 10 points, car :
\[ 1 + \left\lceil\frac{16.6875}{2}\right\rceil = 10 \]
La distance entre deux échantillons de son profil est donc de 16.6875/9, soit environ 1.85 m. Le premier de ces échantillons vaut 384.75 m, le second vaut 384.6875 m, et ainsi de suite. La table ci-dessous donne la valeur de la totalité des échantillons, de même que la différence entre chaque échantillon et son prédécesseur (ou l'altitude 0 pour le premier) :
| Index | Valeur | Différence |
|---|---|---|
| 0 | 384.75 | 384.75 |
| 1 | 384.6875 | -0.0625 |
| 2 | 384.5625 | -0.125 |
| 3 | 384.5 | -0.0625 |
| 4 | 384.4375 | -0.0625 |
| 5 | 384.375 | -0.0625 |
| 6 | 384.3125 | -0.0625 |
| 7 | 384.25 | -0.0625 |
| 8 | 384.125 | -0.125 |
| 9 | 384.0625 | -0.0625 |
Comme on le voit, la différence entre un échantillon et son prédécesseur se représente sans difficulté au format Q0.4. Ce profil peut donc être représenté de manière compressée, au moyen de 4 valeurs de 16 bits, données dans la table ci-dessous :
| Valeur (en base 16) | Signification | Échantillon(s) |
|---|---|---|
180C |
384.75 | 0 |
FEFF |
-0.0625, -0.125, -0.0625, -0.0625 | 1 à 4 |
FFFE |
-0.0625, -0.0625, -0.0625, -0.125 | 5 à 8 |
F000 |
-0.0625, 0, 0, 0 | 9 |
Cette version compressée permet de n'utiliser que 4 valeurs plutôt que 10 pour représenter le profil, soit un gain appréciable de 60%.
2.2.7. Ensembles d'attributs OSM
Les ensembles d'attributs OSM sont représentés au moyen de valeurs de 64 bits, comme décrit à l'étape 2. Ces ensembles sont placés dans un tableau, et chaque arête contient l'identité (index) de l'ensemble des attributs qui lui sont attachés.
3. Mise en œuvre Java
Les trois classes à écrire pour cette étape sont uniquement destinées à être utilisées par la classe Graph représentant le graphe JaVelo, qui sera réalisée à l'étape suivante. Dès lors, il serait possible — et même souhaitable — d'en faire des classes package private, invisibles hors de leur paquetage. Nous avons toutefois choisi de les définir comme publiques, car sans cela, il ne nous serait pas possible de vous fournir un fichier de vérification de signatures.
Afin de ne pas devoir définir explicitement les attributs et constructeurs de ces classes, nous avons de plus choisi d'en faire des enregistrements. Cette utilisation de la notion d'enregistrement est discutable, mais peu gênante étant donné que ces classes ne devraient pas être utilisée pour autre chose que la mise en œuvre de Graph.
Finalement, nous avons choisi de ne jamais valider explicitement les identités (index) des différentes valeurs représentées — nœuds, arêtes, etc. — sachant que l'utilisation d'un index invalide produira de toute manière une IndexOutOfBoundsException, levée par la bibliothèque Java, ce qui semble suffisant.
Avant de décrire les trois classes à mettre en œuvre pour cette étape, il convient toutefois de présenter rapidement la classe Buffer et ses sous-classes, indispensables à cette étape.
3.1. Classe Buffer et ses sous-classes
La bibliothèques Java offre, dans le paquetage java.nio, un certain nombre de classes représentant ce que l'on nomme une mémoire tampon (buffer). Pour l'instant, vous pouvez admettre qu'une mémoire tampon est similaire à un tableau.
Pour JaVelo, nous utiliserons les quatre classes ci-dessous, représentant chacune un type de mémoire tampon différent :
ByteBuffer, similaire à un tableau de typebyte[],ShortBuffer, similaire à un tableau de typeshort[],IntBuffer, similaire à un tableau de typeint[],LongBuffer, similaire à un tableau de typelong[].
Toutes ces classes héritent de la classe abstraite Buffer.
Les sous-classes de Buffer possèdent un très grand nombre de méthodes, mais nous n'en utiliserons qu'un minuscule sous-ensemble. Dans cette étape, vous n'aurez besoin que de :
- la méthode
capacity, qui retourne la taille de la mémoire tampon — similaire à l'attributlengthdes tableaux, - différentes méthodes dont le nom commence par (ou est simplement)
getet qui retournent un élément à une position donnée — similaire à l'opération d'indexation des tableaux, notée[]en Java, - différentes variantes de méthodes statiques nommées
wrap, qui permettent en quelque sorte de transformer un tableau Java normal en une mémoire tampon de même type et de même contenu, et qui seront utiles pour les tests (uniquement), - d'autres méthodes utiles pour les tests uniquement, présentées à la §3.5.
Les méthodes get permettent d'obtenir la valeur d'un élément d'une mémoire tampon dont on connaît l'index. Par exemple, la classe IntBuffer offre une méthode get qui, étant donné un index, retourne l'entier de type int à cet index. Ainsi, l'extrait de programme suivant permet d'obtenir le dernier élément d'un IntBuffer contenant les éléments 1, 2 et 3 :
IntBuffer b = IntBuffer.wrap(new int[]{1, 2, 3});
int last = b.get(b.capacity() - 1); // vaut 3
Cet extrait de programme est très similaire à celui qu'on écrirait pour obtenir le dernier élément d'un tableau d'entiers de type int[] :
int[] b = new int[]{1, 2, 3};
int last = b[b.length - 1]; // vaut 3
Les autres classes mentionnées plus haut possèdent également une méthode get qui a le même comportement mais retourne une valeur du type correspondant à la mémoire tampon : byte pour ByteBuffer, short pour ShortBuffer et long pour LongBuffer.
La classe ByteBuffer, et elle seule, offre de plus des méthodes permettant de combiner plusieurs octets pour obtenir une valeur d'un autre type. Par exemple, la méthode getShort, à qui on passe l'index d'un octet (8 bits) du tableau, combine cet octet avec son successeur en une unique valeur de type short (16 bits) qu'elle retourne. Ainsi, l'extrait de programme suivant combine les octets d'index 1 et 2 du tampon b en une seule valeur de type short, puis l'affiche en hexadécimal (base 16) :
ByteBuffer b = ByteBuffer.wrap(new byte[]{0x12, 0x34, 0x56});
short s = b.getShort(1);
System.out.println(Integer.toHexString(s)); // affiche 3456
En plus de getShort, ByteBuffer offre également la méthode getInt, qui a un comportement similaire mais combine 4 octets (de 8 bits chacun) pour obtenir une unique valeur de type int (de 32 bits).
3.2. Enregistrement GraphNodes
L'enregistrement GraphNodes du paquetage ch.epfl.javelo.data, public, représente le tableau de tous les nœuds du graphe JaVelo. Il possède un seul attribut :
IntBuffer buffer, la mémoire tampon contenant la valeur des attributs de la totalité des nœuds du graphe.
Dans la mémoire tampon, chaque nœud est représenté par trois valeurs de type int, qui sont, dans l'ordre :
- la coordonnée E du nœud,
- la coordonnée N du nœud,
- le nombre d'arêtes sortantes du nœud et l'index de la première d'entre elles, empaquetés dans une seule valeur de type
int, comme décrit à la §2.2.2.
Il en découle que la coordonnée E du nœud d'identité 0 se trouve à l'index 0 de la mémoire tampon, la coordonnée N de ce nœud à l'index 1, son nombre d'arêtes sortantes et l'identité de la première d'entre elles à l'index 2. Ces trois valeurs sont suivies par la coordonnée E du nœud d'identité 1 (à l'index 3), la coordonnée N du même nœud (à l'index 4), et ainsi de suite. Les conseils de programmation plus bas expliquent comment écrire clairement le code accédant à ces valeurs.
GraphNodes offre les méthodes publiques suivantes, qui ont principalement pour but de donner accès aux différents attributs d'un nœud dont on connaît l'identité :
int count(), qui retourne le nombre total de nœuds,double nodeE(int nodeId), qui retourne la coordonnée E du nœud d'identité donnée,double nodeN(int nodeId), qui retourne la coordonnée N du nœud d'identité donnée,int outDegree(int nodeId), qui retourne le nombre d'arêtes sortant du nœud d'identité donné,int edgeId(int nodeId, int edgeIndex), qui retourne l'identité de laedgeIndex-ième arête sortant du nœud d'identiténodeId.
La méthode edgeId ne valide pas l'index de l'arête qu'on lui passe. Il paraît toutefois judicieux d'utiliser une assertion Java pour vérifier qu'il est valide, comme décrit dans les conseils de programmation plus bas.
3.2.1. Conseils de programmation
- Accès aux attributs des nœuds
Le fait que chaque nœud soit représenté par trois éléments (de type
int) de la mémoire tampon a deux conséquences :- la taille de la mémoire tampon, fournie par la méthode
capacity, doit être divisée par trois pour obtenir le nombre total de nœuds, et - toutes les méthodes qui reçoivent une identité de nœud doivent faire un calcul pour déterminer l'index de l'élément de la mémoire tampon qu'elles doivent lire.
Pour que le code des méthodes de
GraphNodessoit clair, il faut absolument nommer les constantes utilisées. Une manière simple de faire cela consiste à définir une constante par attribut d'un nœud, et de définir ces constantes les unes en fonction des autres, en écrivant quelque chose comme :private static final int OFFSET_E = 0; private static final int OFFSET_N = OFFSET_E + 1; private static final int OFFSET_OUT_EDGES = OFFSET_N + 1; private static final int NODE_INTS = OFFSET_OUT_EDGES + 1;
Les constantes dont le nom commence par
OFFSETcontiennent la position des différents attributs dans un nœud, et la constanteNODE_INTSdonne le nombre d'entiers nécessaires pour représenter un nœud, à savoir 3. - la taille de la mémoire tampon, fournie par la méthode
- Validation des index des arêtes
La méthode
edgeIdfait l'hypothèse que l'index de l'arête qu'on lui passe est valide, c.-à-d. qu'il est compris entre 0 (inclus) et le nombre d'arêtes sortant du nœud (exclus). Vous pouvez toutefois, si vous le désirez, ajouter une assertion Java vérifiant cela, en écrivant par exemple :assert 0 <= edgeIndex && edgeIndex < outDegree(nodeId);
ou quelque chose d'équivalent. Notez que si vous faites cela, alors vous devez absolument activer les assertions lorsque vous lancez votre programme, en passant l'option
-eaà Java, comme expliqué au bas de notre guide pour IntelliJ ou Eclipse.
3.3. Enregistrement GraphSectors
L'enregistrement GraphSectors du paquetage ch.epfl.javelo.data, public, représente le tableau contenant les 16384 secteurs de JaVelo. Il possède un seul attribut :
ByteBuffer buffer, la mémoire tampon contenant la valeur des attributs de la totalité des secteurs.
Chaque secteur est représenté par une valeur de type int suivi d'une valeur de type short, comme expliqué à la §2.2.3.
En plus d'une méthode publique décrite plus bas, GraphSectors possède un enregistrement imbriqué nommé Sector, représentant un secteur et doté uniquement des deux attributs suivants :
int startNodeId, l'identité (index) du premier nœud du secteur,int endNodeId, l'identité (index) du nœud situé juste après le dernier nœud du secteur.
Notez bien que si, dans le grand tableau, les secteurs sont représentés par un index de nœud et une longueur, ils sont représentés par deux index de nœuds dans l'enregistrement Sector. Cela est dû au fait que la première représentation est plus compacte, mais la seconde plus agréable à utiliser.
GraphSectors ne fournit qu'une seule méthode publique :
List<Sector> sectorsInArea(PointCh center, double distance), qui retourne la liste de tous les secteurs ayant une intersection avec le carré centré au point donné et de côté égal au double (!) de la distance donnée.
Pour mémoire, vous pouvez considérer pour l'instant qu'une liste n'est rien d'autre qu'un tableau dynamique, et votre méthode sectorsInArea peut donc retourner une valeur de type ArrayList<Sector>.
3.3.1. Conseils de programmation
Contrairement à ceux des nœuds, les attributs des secteurs n'ont pas tous la même taille : le premier fait 32 bits, le second 16.
Pour cette raison, la mémoire tampon utilisée par GraphSectors est de type ByteBuffer, et il faut utiliser les méthodes getShort et getInt pour accéder aux éléments. Prêtez attention au fait que les index à passer à ces méthodes sont des index d'octets, ce qui implique que les constantes à définir pour y accéder (OFFSET_…) doivent être exprimées en octets. Pour les définir, aidez-vous des constantes Short.BYTES et Integer.BYTES, qui donnent le nombre d'octets contenus respectivement dans un entier de type short et de type int.
Notez finalement que les deux attributs d'un secteur doivent être interprétés de manière non signée.
Pour le premier d'entre eux, qui donne l'index du premier nœud du secteur, ce détail peut être ignoré car le graphe de la Suisse entière ne contient « que » 10 millions de nœuds, ce qui est bien inférieur à la plus grande valeur positive représentable par un entier de type int.
Par contre, pour le second attribut, qui donne la taille du secteur, il faut prêter attention à cela et utiliser la méthode toUnsignedInt de la classe Short pour effectivement interpréter les 16 bits de manière non signée.
3.4. Enregistrement GraphEdges
L'enregistrement GraphEdges du paquetage ch.epfl.javelo.data, public, représente le tableau de toutes les arêtes du graphe JaVelo. Il possède les attributs suivants :
ByteBuffer edgesBuffer, la mémoire tampon contenant la valeur des attributs figurant dans la première table de la §2.2.4 pour la totalité des arêtes du graphe,IntBuffer profileIds, la mémoire tampon contenant la valeur des attributs figurant dans la seconde table de la §2.2.4 pour la totalité des arêtes du graphe,ShortBuffer elevations, la mémoire tampon contenant la totalité des échantillons des profils, compressés ou non.
Pour chaque arête du graphe, edgesBuffer contient donc, dans l'ordre : un entier de type int (sens de l'arête et identité du nœud destination), un entier de type short (longueur de l'arête), un entier de type short (dénivelé positif total) et un entier de type short (identité de l'ensemble des attributs OSM). De son côté, profileIds contient, pour chaque arête du graphe, un seul entier de type int (type du profil et index du premier échantillon).
La raison pour laquelle ces deux ensembles d'attributs sont répartis dans deux mémoires tampons séparées est que cela permet d'accélérer la recherche d'itinéraire. En effet, seul le contenu de edgesBuffer est nécessaire à cette recherche, comme nous le verrons ultérieurement.
GraphEdges offre les méthodes publiques suivantes, qui donnent accès aux différentes caractéristiques d'une arête dont on connaît l'identité :
boolean isInverted(int edgeId), qui retourne vrai ssi l'arête d'identité donnée va dans le sens inverse de la voie OSM dont elle provient,int targetNodeId(int edgeId), qui retourne l'identité du nœud destination de l'arête d'identité donnée,double length(int edgeId), qui retourne la longueur, en mètres, de l'arête d'identité donnée,double elevationGain(int edgeId), qui retourne le dénivelé positif, en mètres, de l'arête d'identité donnée,boolean hasProfile(int edgeId), qui retourne vrai ssi l'arête d'identité donnée possède un profil,float[] profileSamples(int edgeId), qui retourne le tableau des échantillons du profil de l'arête d'identité donnée, qui est vide si l'arête ne possède pas de profil,int attributesIndex(int edgeId), qui retourne l'identité de l'ensemble d'attributs attaché à l'arête d'identité donnée.
3.4.1. Conseils de programmation
La méthode profileSamples doit déterminer le nombre d'échantillons du profil de l'arête en fonction de sa longueur. Pour cela, elle doit utiliser la formule donnée à la §2.2.5, mais en travaillant uniquement avec des valeurs au format UQ28.4.
En d'autres termes, la méthode profileSamples doit utiliser la méthode ceilDiv de Math2 en lui passant la longueur de l'arête au format UQ28.4 et la constante 2 au même format — qui s'obtient au moyen de la méthode ofInt de Q28_4.
3.5. Tests
Comme pour l'étape précédente, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.
Pour écrire vos tests, vous pouvez vous aider des méthodes wrap des sous-classes de Buffer pour définir des valeurs de test. Par exemple, l'extrait de test suivant utilise l'une de ces méthodes pour créer une mémoire tampon de type IntBuffer contenant la représentation d'un seul nœud situé à l'origine du système de coordonnées suisse et doté de 2 arêtes sortantes, la première ayant l'identité 123416, la seconde ayant donc l'identité 123516.
IntBuffer b = IntBuffer.wrap(new int[]{
2_600_000 << 4,
1_200_000 << 4,
0x2_000_1234
});
GraphNodes ns = new GraphNodes(b);
assertEquals(1, ns.count());
assertEquals(2_600_000, ns.nodeE(0));
assertEquals(1_200_000, ns.nodeN(0));
assertEquals(2, ns.outDegree(0));
assertEquals(0x1234, ns.edgeId(0, 0));
assertEquals(0x1235, ns.edgeId(0, 1));
Les variantes de la méthode wrap conviennent bien pour les mémoires tampons contenant des valeurs de même taille, mais pas pour celles contenant des valeurs de taille différente. Dans ce cas, il faut utiliser la méthode allocate pour créer une mémoire tampon de type ByteBuffer, puis la remplir au moyen des méthodes putShort et putInt, qui permettent d'écrire des valeurs de type short et int à des index donnés.
L'extrait de test ci-dessous utilise cette technique pour créer un tableau contenant une seule arête. Cela fait, elle crée les autres mémoires tampons nécessaires à la construction d'une instance de GraphEdges, dont elle teste ensuite les méthodes. Notez que le profil utilisé est celui donné en exemple à la §2.2.6, mais les échantillons attendus (expectedSamples) sont dans l'ordre inverse, car l'arête est déclarée comme allant dans le sens inverse de la voie OSM.
(Remarquez au passage l'utilisation de la méthode assertArrayEquals de JUnit pour vérifier que le contenu de deux tableaux est bien identique.)
ByteBuffer edgesBuffer = ByteBuffer.allocate(10);
// Sens : inversé. Nœud destination : 12.
edgesBuffer.putInt(0, ~12);
// Longueur : 0x10.b m (= 16.6875 m)
edgesBuffer.putShort(4, (short) 0x10_b);
// Dénivelé : 0x10.0 m (= 16.0 m)
edgesBuffer.putShort(6, (short) 0x10_0);
// Identité de l'ensemble d'attributs OSM : 2022
edgesBuffer.putShort(8, (short) 2022);
IntBuffer profileIds = IntBuffer.wrap(new int[]{
// Type : 3. Index du premier échantillon : 1.
(3 << 30) | 1
});
ShortBuffer elevations = ShortBuffer.wrap(new short[]{
(short) 0,
(short) 0x180C, (short) 0xFEFF,
(short) 0xFFFE, (short) 0xF000
});
GraphEdges edges =
new GraphEdges(edgesBuffer, profileIds, elevations);
assertTrue(edges.isInverted(0));
assertEquals(12, edges.targetNodeId(0));
assertEquals(16.6875, edges.length(0));
assertEquals(16.0, edges.elevationGain(0));
assertEquals(2022, edges.attributesIndex(0));
float[] expectedSamples = new float[]{
384.0625f, 384.125f, 384.25f, 384.3125f, 384.375f,
384.4375f, 384.5f, 384.5625f, 384.6875f, 384.75f
};
assertArrayEquals(expectedSamples, edges.profileSamples(0));
4. Résumé
Pour cette étape, vous devez :
- écrire les enregistrements
GraphNodes,GraphSectorsetGraphEdgesselon les indications données ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 11 mars 2022 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !