Données OpenStreetMap
JaVelo – étape 2
1. Introduction
Le but de cette deuxième étape du projet est d'une part d'écrire des classes permettant de travailler avec les données du projet OpenStreetMap — que nous utiliserons pour la planification d'itinéraire — et d'autre part d'écrire différentes classes utilitaires nécessaires ultérieurement.
Avant de commencer à travailler à cette étape, lisez le guide Sauvegarder son travail. Il vous donnera des conseils importants concernant la sauvegarde de votre projet au cours du semestre.
2. Concepts
2.1. OpenStreetMap
OpenStreetMap — souvent abrégé OSM — est un projet visant à créer une base de données géographique du monde entier, librement utilisable et modifiable. OpenStreetMap est donc similaire à Wikipedia, mais pour les données géographiques.
Les données d'OpenStreetMap peuvent être utilisées de nombreuses manières, par exemple pour créer des cartes du monde similaires à celle visible ci-dessous.
Ces données sont extrêmement riches, et la carte ci-dessus ne les affiche de loin pas toutes. En plus du site officiel du projet, il existe donc de nombreux autres sites présentant les mêmes données mais dans un style différent.
Ainsi, la carte ci-dessous provient du projet CyclOSM. On y voit la même région que ci-dessus, mais dans un style adapté au cyclisme : les itinéraires cyclables y sont mis en évidence, de même que les pistes et bandes cyclables, les parkings à vélo, etc.
Pour JaVelo, nous utiliserons les données OSM pour déterminer un itinéraire convenant bien à la pratique du vélo. Il est donc important de comprendre la manière dont elles sont représentées, sujet des sections suivantes.
2.1.1. Modèle de données
La totalité des données OSM est constituée de trois types d'éléments :
- les nœuds (nodes), qui représentent des points à la surface de la Terre,
- les « voies » (ways), qui représentent des séquences ordonnées de nœuds,
- les relations (relations), qui représentent des séquences ordonnées de nœuds, de chemins ou d'autres relations.
Les nœuds sont généralement utilisés pour représenter des objets dont la dimension physique n'est pas importante, comme les arbres, les fontaines, les feux de signalisation, etc. Ils servent de plus d'éléments de base pour les voies, utilisées elles pour représenter soit des données « unidimensionnelles » comme les routes ou les frontières, soit des données bidimensionnelles simples, comme certains bâtiments. Finalement, les relations sont utilisées pour représenter des groupes d'autres éléments liés entre eux, comme l'ensemble des routes formant un itinéraire cyclable ou une ligne de bus.
Chaque élément est identifié par son identité (identity), un entier positif. Il ne peut exister qu'un seul élément d'un type donné ayant une identité donnée, mais il peut très bien exister deux éléments de types différents, p. ex. un nœud et une voie, ayant la même identité.
Les trois types d'éléments ont un petit nombre d'attributs fondamentaux qui leur sont associés et qui sont obligatoires. Par exemple, un nœud possède une position à la surface de la Terre, donnée par sa longitude et sa latitude, une voie possède un ensemble de nœuds, etc. En plus de ce petit nombre d'attributs fondamentaux, il est possible d'attacher à n'importe quel élément OSM un nombre quelconque d'attributs additionnels, qui sont des paires clef/valeur textuelles. La clef et la valeur de chaque paire sont séparées par le signe « égal » (=). Par exemple, l'attribut dont la clef est surface et la valeur asphalt s'écrit surface=asphalt.
Il n'y a aucune restriction quant aux clefs et aux valeurs qu'il est autorisé d'attacher à un élément OSM. Au cours du temps, des conventions sont toutefois adoptées par consensus et ce sont ces conventions qui sont utilisées pour dessiner les cartes présentées plus haut, et que nous utiliserons dans JaVelo.
Par exemple, une convention utilisée depuis le début du projet est que l'attribut dont la clef est highway est attaché aux voies qui représentent des routes. La valeur de cet attribut décrit le type de route dont il s'agit. Ainsi, la valeur motorway est utilisée pour les autoroutes, dessinées en rouge sur la carte OSM standard. Les attributs les plus fréquemment utilisés sont répertoriés sur la page Éléments cartographiques du Wiki OSM, auquel les personnes intéressées peuvent jeter un bref coup d'œil si elles le désirent.
Les sections suivantes décrivent plus en détail les trois types d'éléments OSM, et donnent un exemple de chacun d'entre eux.
2.1.2. Nœuds
Un nœud (node) est un point dont la position à la surface de la Terre est donnée par sa longitude et sa latitude, exprimées dans le système WGS84.
Par exemple, le nœud dont l'identité est 5981854153 représente le « Chêne de Napoléon », un arbre célèbre qui se trouve sur le campus de l'UNIL. Un certain nombre d'attributs sont attachés à ce nœud, p. ex. natural=tree qui l'identifie comme étant un arbre, ou name=Chêne de Napoléon qui donne son nom.
Il est possible de connaître la totalité des attributs d'un nœud OSM dont on connaît l'identité en suivant un lien ayant la forme suivante :
https://www.openstreetmap.org/node/<id>
où <id> est l'identité du nœud. Par exemple, pour connaître la totalité des attributs du nœud mentionné ci-dessus, il suffit de suivre le lien https://www.openstreetmap.org/node/5981854153
2.1.3. Voies
Une « voie » (way) est une séquence ordonnée de nœuds OSM.
Par exemple, la voie dont l'identité est 88954910 représente un bout de l'avenue Auguste-Piccard sur le campus de l'EPFL. Elle est composée de 7 nœuds et dotée d'un certain nombre d'attributs. Parmi ceux-ci, on trouve maxspeed=30, qui donne la vitesse maximale à laquelle il est autorisé de rouler sur cette route, et oneway=yes, qui signifie qu'il s'agit d'une route à sens unique.
Comme cet exemple l'illustre, il peut être nécessaire de tenir compte de l'ordre des nœuds d'une voie pour interpréter correctement certains attributs. Ainsi lorsque l'attribut oneway=yes est attaché à une voie, cela signifie qu'elle représente une route à sens unique et que le sens de circulation est identique à l'ordre des nœuds de la voie. Ce même attribut peut avoir la valeur -1 (oneway=-1), qui signifie que le sens de circulation est l'inverse de l'ordre des nœuds.
Comme pour les nœuds, il est possible de connaître la totalité des attributs d'une voie OSM en suivant un lien ayant la forme suivante :
https://www.openstreetmap.org/way/<id>
où <id> est l'identité de la voie.
2.1.4. Relations
Une relation (relation) est une séquence d'autres éléments OSM : nœuds, voies ou relations.
Par exemple, la relation dont l'identité est 28063 représente l'étape 6 de la route numéro 1 de « La Suisse à vélo », qui relie Montreux à Morges en passant devant l'EPFL. Parmi les attributs qui lui sont attachés, on trouve route=bicycle, qui déclare que la relation représente un itinéraire cyclable, ou encore network=ncn, qui nous apprend qu'il s'agit d'une route nationale, NCN signifiant national cycling network.
Sans surprise, il est possible de connaître la totalité des attributs de cette relation en suivant le lien https://www.openstreetmap.org/relation/28063, qui a une forme similaire à ceux présentés plus haut.
Pour JaVelo, les relations sont importantes car, comme l'exemple ci-dessus l'illustre, elles permettent d'identifier les itinéraires cyclables officiels. Par définition, ces itinéraires devraient être bien adaptés aux cyclistes, et donc favorisés par JaVelo.
2.1.5. Pré-traitement des données OSM
Même s'il serait techniquement possible d'écrire un projet comme JaVelo en utilisant directement les données brutes d'OpenStreetMap, cela ne serait pas très efficace, pour deux raisons.
Premièrement, une grande partie des données OSM — p. ex. les contours des bâtiments — n'est d'aucune utilité pour choisir une route agréable à parcourir à vélo.
Deuxièmement, les données OSM ne sont pas organisées de manière à faciliter la recherche d'un itinéraire. Par exemple, étant donné un nœud OpenStreetMap, le seul moyen de déterminer toutes les voies dont ce nœud fait partie est de parcourir la totalité des voies, ce qui est bien entendu très inefficace.
Pour cette raison, les données OSM sont pré-traitées avant d'être utilisées dans JaVelo. Le but de ce pré-traitement est d'une part de ne garder que les données utiles au projet, et d'autre part de les organiser de manière à ce que la recherche d'un itinéraire puisse se faire aussi rapidement que possible. Ce pré-traitement est fait par un programme que vous n'aurez pas à écrire vous même, et seules les données pré-traitées vous seront fournies. Leur format sera décrit à l'étape suivante.
2.2. Projection Web Mercator
Même si cela n'est pas évident au premier coup d'œil, les cartes OpenStreetMap visibles plus haut ne sont pas projetées au moyen de la projection Swiss Grid décrite à l'étape précédente. Cela est compréhensible, car OpenStreetMap est une carte mondiale, et nous avons vu que Swiss Grid ne convient pas à une telle carte en raison des déformations extrêmes qu'elle introduit dès qu'on s'éloigne sensiblement de la Suisse.
La projection utilisée par OpenStreetMap est généralement connue sous le nom de Web Mercator. Comme son nom l'indique, il s'agit d'une variante de la célèbre projection de Mercator, fréquemment utilisée pour les cartes mondiales. L'image ci-dessous montre la Terre entre les latitudes -85° et +85°, projetée au moyen de cette projection.
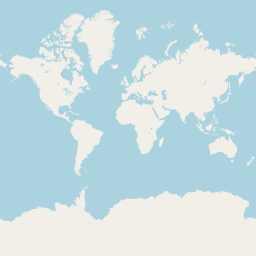
La projection de Mercator a la caractéristique de ne pas permettre la représentation des pôles, car elle les projette à l'infini. Pour cette raison, les cartes l'utilisant sont toujours tronquées à partir d'une latitude donnée, comme celle ci-dessus.
De plus, la projection de Mercator est souvent critiquée, à raison, pour les importantes déformations qu'elle introduit dans les éléments situés aux latitudes élevées. Ainsi, la carte ci-dessus donne l'impression que le Groenland est aussi grand que l'Afrique, alors que cette dernière est en réalité 14 fois plus grande. La page Wikipedia consacrée à la projection de Mercator inclut une animation permettant de bien se rendre compte des déformations introduites, que les personnes intéressées pourront consulter.
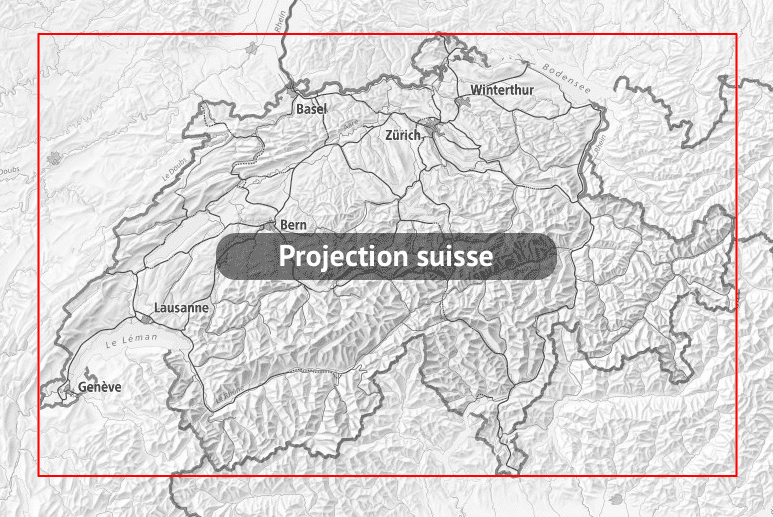
Cela dit, sur le territoire suisse, la différence entre la projection Swiss Grid et la projection Web Mercator n'est pas très importante. Pour s'en rendre compte, on peut cliquer sur l'image ci-dessous afin de visualiser la Suisse projetée alternativement avec chacune de ces projections. La zone entourée en rouge est celle des points dont les coordonnées, dans le système suisse, sont comprises entre E=2 485 000 et E=2 834 000, et entre N=1 075 000 et N=1 296 000. Logiquement, cette zone n'est rectangulaire que dans la projection suisse.
2.3. Coordonnées Web Mercator
Une fois la Terre projeté au moyen de la projection Web Mercator, on peut lui attacher un système de coordonnées cartésien. Ce système, illustré dans l'image ci-dessous, a son origine dans le coin haut-gauche de la projection, tandis que le coin bas-droit possède les coordonnées (1,1).
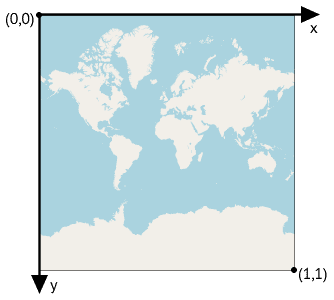
Les coordonnées \((x, y)\) d'un point de longitude \(\lambda\) et de latitude \(\phi\) s'obtiennent au moyen des formules suivantes, dans lesquelles les angles sont en radians :
\begin{align} \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} x & = \frac{1}{2\pi}\left(\lambda + \pi\right)\\[0.5em] y & = \frac{1}{2\pi}\left(\pi - \arsinh(\tan\phi)\right) \end{align}A l'inverse, il est possible d'obtenir la longitude \(\lambda\) et la latitude \(\phi\) d'un point dont on connaît les coordonnées Web Mercator \((x, y)\) au moyen des formules suivantes :
\begin{align} \lambda & = 2\pi\, x - \pi\\[0.5em] \phi & = \arctan\left(\sinh(\pi - 2\pi\, y)\right) \end{align}2.3.1. Coordonnées sur les images
Comme son nom l'indique, le système Web Mercator a été développé à l'origine pour présenter des cartes sur le Web. Ces cartes peuvent être visualisées à différents niveaux de zoom (zoom levels), allant généralement de 0 à 19, voire 20.
Au niveau de zoom 0, la carte de la Terre entière est une image carrée de 256 pixels de côté, qui est celle visible dans les figures 1 et 2. A chaque passage d'un niveau de zoom au suivant, la largeur et la hauteur de cette image doublent. Ainsi, au niveau de zoom 1, la carte fait 512 pixels de côté ; au niveau de zoom 2, elle fait 1024 pixels de côté ; et ainsi de suite. De manière générale, au niveau de zoom \(z\), la carte de la Terre entière est une image de
\[ 256\cdot 2^z = 2^8\cdot 2^z = 2^{8 + z}\]
pixels de côté.
Sachant cela, il est très facile de connaître la position d'un point dont on connaît les coordonnées Web Mercator dans l'image de la carte à un niveau de zoom donné, puisqu'il suffit de multiplier ses coordonnées par la taille de l'image à ce niveau de zoom.
Par exemple, le Chêne de Napoléon a les coordonnées WGS 84 :
\[\lambda=6.5790772, \phi=46.5218976\]
et donc, d'après les formules plus haut, les coordonnées Web Mercator :
\[x=0.518275214444, y=0.353664894749\]
Au niveau de zoom 19, le Chêne de Napoléon se trouve donc à la position (arrondie) :
\[x_{19} = 69 561 722, y_{19} = 47 468 099 \]
dans l'image de 227 = 134 217 728 pixels de côté qui constitue la carte de la Terre entière à ce niveau de zoom.
2.4. Nombres à virgule fixe
La quantité de données à manipuler dans JaVelo est importante, car la planification d'un itinéraire implique de connaître précisément de nombreuses caractéristiques des routes suisses : leur emplacement exact, leur profil en long, leur type, leurs éventuelles restrictions de circulation, etc. Il faut donc prêter une attention particulière à la représentation de ces données et éviter qu'elles ne prennent trop de place en mémoire, ce qui pourrait avoir un impact négatif sur les performances du programme.
Pour cette raison, nous représenterons certaines données comme les distances ou les altitudes au moyen de ce que l'on nomme des nombres à virgule fixe (fixed-point numbers). Afin de comprendre ce concept, voyons comment il pourrait être utilisé pour représenter efficacement la différence d'altitude entre deux points d'une même route situés à 2 m l'un de l'autre. Comme nous le verrons à l'étape suivante, les profils en long sont représentés par de telles différences d'altitude.
2.4.1. Représentation entière
Une première manière de représenter une différence d'altitude entre deux points serait d'utiliser un entier Java de type byte, et de l'interpréter comme d'habitude en complément à deux.
Pour mémoire, avec cette interprétation, une valeur de type byte peut représenter n'importe quel entier compris entre -128 et +127. En supposant que les différences d'altitudes soient exprimées en mètres, nous aurions ainsi la possibilité de représenter des différences d'altitudes entières comprises entre -128 m et +127 m.
Ce choix ne semble pas vraiment optimal, pour deux raisons : d'une part, seules les différences entières sont représentables, et d'autre part la plage couverte est bien trop importante. En effet, si la différence d'altitude entre deux points d'une route situés à 2 mètres l'un de l'autre est de -128 mètres, cela signifie que la pente de la route est de 6400% à cet endroit, or les pentes supérieures à 20% sont rares en pratique.
Pour résoudre ces problèmes, une solution simple est de changer d'unité. On peut ainsi décider de représenter la différence d'altitude en seizièmes de mètres plutôt qu'en mètres. Cela augmente la précision, qui passe à 6.25 cm (1/16 m), tout en permettant encore de représenter des pentes allant jusqu'à 400%, ce qui reste largement suffisant.
2.4.2. Représentation en virgule fixe
Plutôt que de changer d'unité, il est aussi possible de changer la manière dont la valeur de type byte est interprétée. Pour mémoire, nous avons vu au cours que l'interprétation en complément à deux d'une valeur de type byte (8 bits) consiste à associer à chacun des bits un poids dépendant de sa position, poids qui est positif pour tous les bits sauf celui de poids le plus fort, comme illustré ci-dessous :
| Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Poids | \(-128\) | \(64\) | \(32\) | \(16\) | \(8\) | \(4\) | \(2\) | \(1\) |
Par exemple, avec cette interprétation, les 8 bits 10011100 représentent l'entier \(-100\) (car \(-128 + 16 + 8 + 4 = -100\)).
Dans l'interprétation en complément à deux, le poids du bit \(p\) vaut \(±2^{p}\), et le bit 0 a donc un poids de 1. En conséquence, cette interprétation ne permet pas de représenter des valeurs non entières. Pour permettre la représentation de valeurs non entières avec une précision de 1/16, il suffit de décider que le bit 0 a un poids de 1/16 et d'ajuster les autres poids en conséquence :
| Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Poids | \(-8\) | \(4\) | \(2\) | \(1\) | \(\tfrac{1}{2}\) | \(\tfrac{1}{4}\) | \(\tfrac{1}{8}\) | \(\tfrac{1}{16}\) |
Avec cette nouvelle interprétation, le poids du bit \(p\) vaut \(±2^{p - 4}\). Ainsi, les mêmes 8 bits que ci-dessus (10011100) représentent désormais la valeur \(-6.25\) (car \(-8 + 1 + \tfrac{1}{2} + \tfrac{1}{4} = -6.25\)).
Cette manière d'interpréter les bits est tout à fait équivalente à la manière d'interpréter les chiffres d'un nombre écrit dans la notation décimale positionnelle à laquelle nous sommes habitués. La seule différence est que les ordinateurs travaillent en base 2, alors que nous travaillons en base 10. Par exemple, le nombre noté \(3.14\) vaut \(3\cdot 10^0 + 1\cdot 10^{-1} + 4\cdot 10^{-2}\).
Dans la notation décimale usuelle, on utilise le point décimal (ou la virgule décimale) pour séparer les chiffres dont le poids correspond à une puissance de dix positive ou nulle de ceux dont le poids correspond à une puissance de dix négative. Dans l'interprétation des valeurs de type byte présentée ci-dessus, on peut donc imaginer qu'un « point binaire » est placé après le bit 4. En d'autres termes, on pourrait noter la valeur \(-6.25\) comme 1001.1100.
Étant donné que le « point binaire » se trouve toujours à la même position dans une telle interprétation, on dit que les nombres que l'on interprète de la sorte sont à virgule fixe. Pour connaître le nombre de bits utilisés à gauche et à droite du point, on utilise souvent la « notation Q ». Par exemple, l'interprétation ci-dessus serait notée Q4.4, ce qui signifie qu'elle comporte 4 bits à gauche du point, et 4 à droite. Dans cette notation, la lettre Q peut être précédée d'un U si les nombres sont interprétés de manière non signée plutôt qu'en complément à deux.
2.4.3. Nombres à virgule fixe dans JaVelo
Dans JaVelo, nous utiliserons des nombres à virgule fixe pour représenter les données suivantes :
- les altitudes, représentées en mètres au format UQ12.4, qui couvre une plage allant de 0 à 4095.9375 m (inclus)1,
- les différences d'altitudes entre deux points successifs d'une route, représentées en mètres, au format Q0.4 (de -0.5 m à +0.4375 m), ou au format Q4.4 (de -8 m à +7.9375 m),
- les longueurs des segments de routes, représentées en mètres au format UQ12.4 (de 0 à 4095.9375 m),
- les coordonnées suisses (est/nord) des points, représentées en mètres au format Q28.4, qui permet de couvrir (largement) la totalité du territoire suisse.
Sachant que toutes ces données sont en mètres et que nous utilisons systématiquement 4 bits après la virgule, la précision est de 6.25 cm dans tous les cas.
Notez que, comme l'exemple plus haut l'a illustré, notre utilisation des nombres à virgule fixe est totalement équivalente à un changement d'unité. Il est donc tout à fait correct de considérer que les données mentionnées ci-dessus sont toutes exprimées sous forme entière mais en seizième de mètres. N'hésitez pas à adopter ce point de vue s'il vous paraît plus simple à comprendre.
2.5. Fonction échantillonnée
Comme cela a été dit dans l'introduction au projet, une des informations que JaVelo affiche au sujet de l'itinéraire est son profil en long.
Mathématiquement, un profil en long est une fonction continue qui associe une altitude à chaque point de l'itinéraire. Étant donné qu'une fonction continue possède un nombre infini de points, il n'est pas possible de les stocker tous dans la mémoire d'un ordinateur. Au lieu de cela, on ne stocke qu'un nombre fini de ces points, espacés régulièrement, que l'on nomme échantillons (samples).
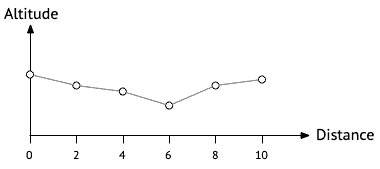
Par exemple, on pourrait imaginer représenter un profil en long au moyen d'échantillons mesurés tous les 2 mètres. Dans ce cas, le profil en long pour un itinéraire de 10 m serait représenté par 6 points : son altitude après 0 m, 2 m, 4 m, 6 m, 8 m et enfin 10 m. L'image ci-dessous présente un exemple de profil en long échantillonné de la sorte.
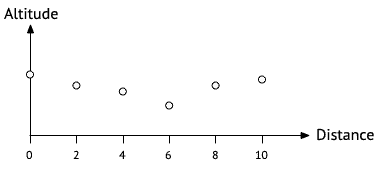
Bien entendu, le fait qu'un profil soit représenté au moyen d'un nombre fini d'échantillons ne signifie pas qu'il n'est défini qu'en ces points. La question se pose donc de savoir comment déterminer la valeur du profil (c.-à-d. l'altitude) des points qui ne font pas partie des échantillons. En d'autres termes, comment obtenir à nouveau une fonction continue à partir d'un nombre discret d'échantillons.
Pour JaVelo, dans un souci de simplicité, nous ferons cela par interpolation linéaire entre les échantillons. L'image ci-dessous montre comment le profil échantillonné présenté ci-dessus peut être rendu continu de cette manière.
3. Mise en œuvre Java
3.1. Classe WebMercator
La classe WebMercator du paquetage ch.epfl.javelo.projection, publique, finale et non instanciable, offre les méthodes statiques suivantes, qui permettent de convertir entre les coordonnées WGS 84 et les coordonnées Web Mercator :
double x(double lon), qui retourne la coordonnéexde la projection d'un point se trouvant à la longitudelon, donnée en radians,double y(double lat), qui retourne la coordonnéeyde la projection d'un point se trouvant à la latitudelat, donnée en radians,double lon(double x), qui retourne la longitude, en radians, d'un point dont la projection se trouve à la coordonnéexdonnée,double lat(double y), qui retourne la latitude, en radians, d'un point dont la projection se trouve à la coordonnéeydonnée.
Tout comme les méthodes de la classe Ch1903, celles de WebMercator ne valident pas leurs arguments, ce travail étant laissé aux classes représentant les points.
3.2. Enregistrement PointWebMercator
L'enregistrement PointWebMercator du paquetage ch.epfl.javelo.projection représente un point dans le système Web Mercator. Ses attributs sont :
double x, la coordonnée x du point,double y, la coordonnée y du point.
Le constructeur (compact) de PointWebMercator valide les coordonnées qu'il reçoit et lève une IllegalArgumentException si l'une d'entre elles n'est pas comprise dans l'intervalle [0;1].
PointWebMercator offre deux méthodes de construction, publiques et statiques :
PointWebMercator of(int zoomLevel, double x, double y), qui retourne le point dont les coordonnées sontxetyau niveau de zoomzoomLevel,PointWebMercator ofPointCh(PointCh pointCh), qui retourne le point Web Mercator correspondant au point du système de coordonnées suisse donné.
Finalement, PointWebMercator offre les méthodes publiques suivantes :
double xAtZoomLevel(int zoomLevel), qui retourne la coordonnéexau niveau de zoom donné,double yAtZoomLevel(int zoomLevel), qui retourne la coordonnéeyau niveau de zoom donné,double lon(), qui retourne la longitude du point, en radians,double lat(), qui retourne la latitude du point, en radians,PointCh toPointCh(), qui retourne le point de coordonnées suisses se trouvant à la même position que le récepteur (this) ounullsi ce point n'est pas dans les limites de la Suisse définies parSwissBounds.
3.2.1. Conseils de programmation
Les méthodes xAtZoomLevel et yAtZoomLevel doivent transformer les coordonnées « normales » du point, comprises entre 0 et 1, en coordonnées de l'image de la carte au niveau de zoom donné. Comme nous l'avons vu à la §2.3.1, cela peut se faire au moyen d'une simple multiplication par une puissance de deux entière, qui dépend du niveau de zoom.
Une telle multiplication pourrait théoriquement se faire en combinant l'opérateur de multiplication (*) avec la méthode pow de Math, qui permet d'élever une valeur à une certaine puissance. Il est toutefois possible de faire mieux ici, grâce à la méthode scalb(x,y) de Math, qui calcule \(x\cdot2^y\) de manière très efficace2.
La méthode scalb accepte également des valeurs négatives en second argument, ce qui permet de diviser très efficacement une valeur par une puissance de deux entière. Cela est très utile pour écrire la méthode of.
3.3. Classe Bits
La classe Bits du paquetage ch.epfl.javelo, publique, finale et non instanciable, contient deux méthodes permettant d'extraire une séquence de bits d'un vecteur de 32 bits :
int extractSigned(int value, int start, int length), qui extrait du vecteur de 32 bitsvaluela plage delengthbits commençant au bit d'indexstart, qu'elle interprète comme une valeur signée en complément à deux, ou lèveIllegalArgumentExceptionsi la plage est invalide (voir ci-dessous)int extractUnsigned(int value, int start, int length), qui fait la même chose que la méthode précédente, à deux différences près : d'une part, la valeur extraite est interpretée de manière non signée, et d'autre part l'exceptionIllegalArgumentExceptionest également levée silengthvaut 32.
Ces deux méthodes considèrent que la plage de bits décrite par les arguments start et length est valide si et seulement si elle est totalement incluse dans l'intervalle allant de 0 à 31 (inclus).
La raison pour laquelle extractUnsigned exige de plus que la longueur de cette plage ne soit pas égale à 32 est qu'il n'est pas possible de représenter une valeur de 32 bits non signée au moyen du type int en Java.
3.3.1. Conseils de programmation
Une manière simple et efficace d'extraire une séquence de bits consiste à effectuer deux décalages successifs :
- un premier décalage à gauche afin d'éjecter tous les bits de poids supérieur à ceux qu'on désire extraire,
- un second décalage à droite afin d'éjecter tous les bits de poids inférieur à ceux qu'on désire extraire et, dans le même temps, de placer les bits à extraire à la bonne position.
Par exemple, imaginons que l'on désire extraire des 32 bits ci-dessous, stockés dans un entier de type int, les 4 bits mis en évidence, à savoir ceux d'index 8 à 11 :
11001010111111101011101010111110
On commence par effectuer un décalage à gauche pour éjecter tous les bits se trouvant à gauche du premier que l'on désire conserver. Il y en a 20, et après avoir décalé la valeur ci-dessous de 20 bits à gauche, on obtient :
10101011111000000000000000000000
les bits soulignés étant ceux insérés par le décalage. Cette valeur peut maintenant être décalée à droite afin de simultanément éjecter les bits se trouvant à droite du dernier que l'on désire extraire et de ramener ceux-ci à la bonne position. Il y a 28 de ces bits, et après avoir décalé la valeur ci-dessus de 28 bits à droite, on obtient :
00000000000000000000000000001010
Une fois encore, les bits soulignés sont ceux insérés par le décalage.
Grâce à cette séquence de deux décalages, on a effectivement réussi à extraire les 4 bits désirés. Il faut noter que le décalage à droite utilisé ci-dessus était un décalage logique. Si on avait utilisé un décalage arithmétique, alors les bits insérés auraient été des copies du bit de poids fort de la valeur avant décalage, 1 ci-dessus. On aurait alors obtenu le résultat suivant :
11111111111111111111111111111010
qui correspond à une extraction de bits signée.
En d'autres termes, les méthodes extractSigned et extractUnsigned consistent toutes deux en un décalage à gauche suivi d'un décalage à droite. La seule différence est que dans le premier cas le décalage à droite est arithmétique, alors que dans le second il est logique.
3.4. Classe Q28_4
La classe Q28_4 du paquetage ch.epfl.javelo, publique, finale et non instanciable, contient les méthodes statiques suivantes, qui permettent de convertir des nombres entre la représentation Q28.4 et d'autres représentations :
int ofInt(int i), qui retourne la valeur Q28.4 correspondant à l'entier donné,double asDouble(int q28_4), qui retourne la valeur de typedoubleégale à la valeur Q28.4 donnée,float asFloat(int q28_4), qui retourne la valeur de typefloatcorrespondant à la valeur Q28.4 donnée.
Notez que ces méthodes sont triviales à écrire au moyen des opérateurs de décalage (<< et >>) ou de la méthode scalb, en fonction des cas.
3.5. Classe Functions
La classe Functions du paquetage ch.epfl.javelo, publique, finale et non instanciable, contient des méthodes permettant de créer des objets représentant des fonctions mathématiques des réels vers les réels, c.-à-d. de type \(\mathbb{R}\rightarrow\mathbb{R}\).
Ces fonctions sont représentées par des valeurs de type DoubleUnaryOperator, une interface de la bibliothèque standard Java qui correspond assez directement à ce type de fonctions, comme expliqué dans les conseils de programmation plus bas.
Les méthodes offertes par Functions, publiques et statiques, sont :
DoubleUnaryOperator constant(double y), qui retourne une fonction constante, dont la valeur est toujoursy,DoubleUnaryOperator sampled(float[] samples, double xMax), qui retourne une fonction obtenue par interpolation linéaire entre les échantillonssamples, espacés régulièrement et couvrant la plage allant de 0 àxMax; lèveIllegalArgumentExceptionsi le tableausamplescontient moins de deux éléments, ou sixMaxest inférieur ou égal à 0.
Lorsqu'on dit que les échantillons samples couvrent la plage allant de 0 à xMax, cela signifie que le premier d'entre eux donne la valeur de la fonction en 0, le dernier donne sa valeur à xMax, et les éventuels échantillons restants sont répartis régulièrement entre ces deux extrêmes. Notez que la fonction retournée par sampled est également définie hors de l'intervalle allant de 0 à xMax : lorsque son argument est négatif, sa valeur est celle du premier échantillon, et lorsque son argument est supérieur à xMax, sa valeur est celle du dernier échantillon.
3.5.1. Conseils de programmation
Afin d'illustrer comment un objet de type DoubleUnaryOperator peut représenter une fonction mathématique des réels vers les réels, considérons la classe F ci-dessous qui implémente cette interface et fournit une définition pour sa seule méthode abstraite, applyAsDouble :
public final class F implements DoubleUnaryOperator {
@Override
public double applyAsDouble(double x) {
return x * x;
}
}
Une instance de cette classe se comporte de manière très similaire à la fonction mathématique d'élévation du carré définie ainsi :
\[ f(x) = x^2 \]
En effet, en appelant la méthode applyAsDouble d'une instance de F en lui passant un nombre quelconque, on obtient ce nombre au carré, exactement comme si on appelait la fonction (mathématique) \(f\) ci-dessus. Ainsi, l'extrait de code ci-dessous affiche 1.44 :
DoubleUnaryOperator f = new F(); System.out.println(f.applyAsDouble(1.2));
Comme cet exemple le suggère, les méthodes constant et sampled retournent simplement une instance d'une classe représentant un type de fonction particulier.
Ainsi, constant retourne une nouvelle instance d'une classe nommée Constant, privée et imbriquée statiquement dans Functions. Cette classe implémente bien entendu l'interface DoubleUnaryOperator et sa redéfinition de la méthode applyAsDouble retourne toujours la même valeur, passée au constructeur de Constant. En d'autres termes, la méthode constant et la classe Constant peuvent se définir ainsi :
public final class Functions {
public static DoubleUnaryOperator constant(double y) {
return new Constant(y);
}
private static final class Constant
implements DoubleUnaryOperator {
// … attribut(s) et constructeur
// … méthode applyAsDouble
}
}
Notez que la classe Constant pourrait même être un enregistrement, ce qui la rendrait encore plus concise.
La méthode sampled peut s'écrire de manière similaire, et simplement retourner une nouvelle instance d'une classe nommée Sampled, également privée et imbriquée statiquement dans Functions.
Nous verrons plus tard dans le cours le concept de lambda, qui permet d'écrire les méthodes constant et sampled de manière beaucoup plus concise. Les personnes qui connaîtraient déjà ce concept peuvent bien entendu l'utiliser si elles le désirent.
3.6. Type énuméré Attribute (fourni)
Le type énuméré Attribute, du paquetage ch.epfl.javelo.data, public, représente les différents attributs OpenStreetMap attachés aux éléments (nœuds, voies et relation) qui seront utiles au projet.
Pour faciliter votre travail, ce type énuméré vous est fourni dans une archive Zip à importer dans votre projet.
En examinant ce type énuméré, vous constaterez qu'un objet de type Attribute est constitué d'une clef key et d'une valeur value. La clef et la valeur sont des chaînes de caractères.
Notez que comme tout type énuméré en Java, Attribute hérite implicitement de la classe Enum de la bibliothèque standard Java. Cela signifie, entre autres, que ses valeurs sont dotées de la méthode ordinal qui retourne leur position dans le type énuméré, à partir de 0. Par exemple, appliquée à HIGHWAY_TRACK, cette méthode retourne 1 car HIGHWAY_TRACK est le second élément du type énuméré.
La méthode ordinal sera utile pour écrire la classe AttributeSet, décrite ci-après.
3.7. Enregistrement AttributeSet
L'enregistrement AttributeSet du paquetage ch.epfl.javelo.data, public, représente un ensemble d'attributs OpenStreetMap. Cet enregistrement possède un unique attribut :
long bits, qui représente le contenu de l'ensemble au moyen d'un bit par valeur possible ; c'est-à-dire que le bit d'index b de cette valeur vaut 1 si et seulement si l'attribut b est contenu dans l'ensemble.
Par exemple, l'ensemble contenant uniquement les attributs HIGHWAY_TRACK et TRACKTYPE_GRADE1 est représenté par une valeur de type long dans laquelle seuls les bits d'index 1 et 17 valent 1, car HIGHWAY_TRACK est à l'index 1 dans le type énuméré Attribute, tandis que TRACKTYPE_GRADE1 y est à l'index 17.
Le constructeur compact de AttributeSet lève une IllegalArgumentException si la valeur passée au constructeur contient un bit à 1 qui ne correspond à aucun attribut valide.
AttributeSet offre une méthode de construction, publique et statique, permettant de construire un ensemble contenant un certain nombre d'attributs :
AttributeSet of(Attribute... attributes), qui retourne un ensemble contenant uniquement les attributs donnés en argument.
En plus de ces méthodes statiques, AttributeSet offre les méthodes publiques suivantes :
boolean contains(Attribute attribute), qui retourne vrai ssi l'ensemble récepteur (this) contient l'attribut donné,boolean intersects(AttributeSet that), qui retourne vrai ssi l'intersection de l'ensemble récepteur (this) avec celui passé en argument (that) n'est pas vide.
De plus, la classe AttributeSet redéfinit la méthode toString afin qu'elle retourne une chaîne composée de la représentation textuelle des éléments de l'ensemble entourés d'accolades ({}) et séparés par des virgules. Les éléments doivent impérativement apparaître dans l'ordre dans lequel ils sont déclarés dans le type énuméré Attribute. Le test JUnit ci-dessous, qui doit s'exécuter avec succès, illustre le fonctionnement de cette méthode :
AttributeSet set =
AttributeSet.of(TRACKTYPE_GRADE1, HIGHWAY_TRACK);
assertEquals("{highway=track,tracktype=grade1}",
set.toString());
3.7.1. Conseils de programmation
- Masques
Dans plusieurs méthodes de la classe
AttributeSetil est nécessaire d'obtenir le masque correspondant à un attribut, c.-à-d. la valeur de typelongdont tous les bits valent 0 sauf celui dont l'index correspond à l'attribut.Ce masque s'obtient bien entendu par décalage de la constante 1, mais il faut faire très attention à ce que cette constante ait le type
long! En d'autres termes, il faut écrire le code ainsi :Attribute a = …; long mask = 1L << a.ordinal();
où
1Lreprésente la constante 1 mais de typelong. Si on oublie leL, alors cette constante a le typeintet la distance de décalage ne peut donc pas être supérieure ou égale à 32.On peut illustrer cela au moyen du test JUnit suivant, qui s'exécute avec succès :
long mask = 1L << 33; assertEquals(0b1000000000000000000000000000000000L, mask);
Par contre, si on remplace le
1Lde la première ligne par1, le test échoue ! En effet, dans ce cas, la valeur à décaler (1) a le typeint, et la distance de décalage (33) est donc interprétée modulo 32 par Java. Le décalage obtenu n'est donc pas de 33 bits, mais de 1 bit, etmaskvaut donc 2 (0b10). - Méthode
toString
Pour écrire la méthode
toString, nous vous conseillons d'utiliser la classeStringJoinerde la bibliothèque Java. Son but est de construire une chaîne à partir d'autres chaînes, en les séparant d'un séparateur et en les entourant d'un préfixe et d'un suffixe. Par exemple, le test JUnit ci-dessous, qui s'exécute avec succès, montre comment utiliser cette classe pour construire la chaîne(1+2+3):StringJoiner j = new StringJoiner("+", "(", ")"); for (int i = 1; i <= 3; i += 1) j.add(Integer.toString(i)); assertEquals("(1+2+3)", j.toString());Pour faire en sorte que les éléments de l'ensemble apparaissent dans leur ordre de déclaration, le plus simple est de parcourir la totalité des attributs existants dans leur ordre de déclaration, mais de n'ajouter à l'instance de
StringJoinerque ceux effectivement présents dans l'ensemble.Notez que le parcours de tous les attributs existants dans leur ordre de déclaration est très simple à faire car la variable
Attribute.ALLcontient justement la liste de tous ces attributs, dans l'ordre désiré. Cette variable a le typeList<Attribute>que vous ne connaissez pas encore mais que vous pouvez pour l'instant considérer comme équivalent àArrayList<Attribute>.
3.8. Tests
À partir de cette étape, nous ne vous fournissons plus de tests unitaires, et il vous faut donc les écrire vous-même.
Nous vous fournissons néanmoins une archive Zip à importer dans votre projet et contenant un fichier nommé SignatureChecks_2.java. La classe qu'il contient fait référence à la totalité des classes et méthodes des étapes 1 et 2, ce qui vous permet de vérifier que leurs noms et types sont corrects. Cela est capital, car la moindre faute à ce niveau empêcherait l'exécution de nos tests unitaires.
Attention : après avoir importé le contenu de cette archive, n'oubliez surtout pas de marquer le répertoire sigcheck comme Sources Root si vous utilisez IntelliJ (voir le point 7 de notre guide), ou de l'ajouter au Java Build Path de votre projet si vous utilisez Eclipse (voir points 5 à 7 de notre guide).
Si vous oubliez de faire cette manipulation, les éventuelles erreurs contenues dans le fichier de vérification de signatures ne seront pas signalées, le rendant ainsi inutile.
Nous vous fournirons de tels fichiers pour toutes les étapes jusqu'à la sixième (incluse), et il vous faudra penser à vérifier systématiquement qu'aucune erreur n'est signalée à leur sujet. Faute de cela, votre rendu pourrait se voir refusé par notre système.
4. Résumé
Pour cette étape, vous devez :
- écrire les classes et enregistrements
WebMercator,PointWebMercator,Bits,Q28_4,FunctionsetAttributeSetselon les indications ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 4 mars 2022 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !
Notes de bas de page
On notera que le format utilisé pour les altitudes ne permet pas de représenter celle de n'importe quel point en Suisse, puisque le plus haut point du pays (le sommet de la pointe Dufour) se trouve à 4634 mètres. Toutefois, pour JaVelo, seule l'altitude des routes praticables à vélo doit être représentable, et une limite à presque 4096 mètres semble largement suffisante.
La raison pour laquelle scalb peut effectuer de manière très efficace une multiplication (ou une division) par une puissance entière de 2 est que les nombres à virgule flottante de type double ou float sont représentés en base 2. Dès lors, multiplier (ou diviser) par une puissance de 2 revient à déplacer le « point binaire », exactement comme en base 10, multiplier ou diviser par une puissance de 10 revient à déplacer le point décimal.
Au passage, notez que la méthode scalb peut être vue comme l'équivalent des opérateurs de décalage de Java (<< et >>), qui permettent également d'effectuer de manière très efficace des multiplications et des divisions par des puissances de 2. La différence est que ces opérateurs ne fonctionnent que sur des valeurs entières, alors que scalb fonctionne sur des valeurs à virgule flottante.