Projection cartographique suisse
JaVelo – étape 1
1. Introduction
Cette première étape du projet JaVelo a pour but principal d'écrire les classes permettant de représenter la position d'un point en Suisse et de transformer ses coordonnées entre le système utilisé en Suisse et le système « mondial » utilisé par le GPS.
Comme toutes les descriptions d'étapes de ce projet, celle-ci commence par une introduction aux concepts nécessaires à sa réalisation (§2), suivie d'une présentation de leur mise en œuvre en Java (§3).
Si vous travaillez en groupe, vous êtes toutefois priés de lire, avant de continuer, les guides Travailler en groupe et Synchroniser son travail, qui vous aideront à bien vous organiser.
2. Concepts
Dans le projet JaVelo il est souvent nécessaire de spécifier la position de points se trouvant sur le territoire suisse. Les sections qui suivent présentent deux manières de représenter de telles positions, chacune utile dans un contexte différent.
2.1. Coordonnées WGS 84
La manière la plus répandue de spécifier la position d'un point à la surface de la Terre consiste à donner ses coordonnées géographiques, qui sont :
- sa longitude \(\lambda\), la distance angulaire du point au méridien origine — un méridien étant un demi-cercle reliant les deux pôles,
- sa latitude \(\phi\), la distance angulaire du point à l'équateur.
Ces coordonnées sont généralement spécifiées dans le système nommé WGS 84, utilisé entre autres par les récepteurs GPS.
Dans ce système, la longitude est comprise entre -180° et +180°, la longitude 0 étant celle du méridien origine, qui passe près de l'observatoire de Greenwich en Angleterre. La latitude d'un point est quant à elle comprise entre -90° et +90°, la latitude 0 étant celle de l'équateur. La figure ci-dessous illustre ces conventions.
Lorsque l'un des deux angles — longitude ou latitude — n'est pas entier, il existe deux conventions pour noter sa partie fractionnaire :
- la notation décimale, dans laquelle la partie fractionnaire est donnée en base dix après le point décimal, comme habituellement en mathématiques — p.ex. 46.5° pour quarante-six degrés et demi,
- la notation sexagésimale, dans laquelle la partie fractionnaire est donnée en minutes et secondes, en base soixante — p.ex. 46° 30' pour quarante-six degrés et 30 minutes, soit quarante-six degrés et demi.
Nous n'utiliserons pas la notation sexagésimale dans ce projet, mais elle apparaîtra parfois dans les descriptions d'étapes. Ainsi, la carte interactive ci-dessous montre la Suisse et une grille des coordonnées WGS 84 utilisant justement cette notation.
Comme on le voit sur cette carte, le territoire suisse se trouve à des longitudes comprises approximativement entre +5.95° et +10.50°, et à des latitudes comprises approximativement entre +45.81° et +47.81°.
Les coordonnées géographiques sont un exemple de ce que l'on nomme des coordonnées sphériques, que l'on peut voir comme une généralisation à trois dimensions des coordonnées polaires. De telles coordonnées conviennent particulièrement bien pour décrire la position de points se trouvant à la surface d'une sphère. La Terre étant (presque) sphérique, il n'est pas surprenant que ce type de coordonnées se soit imposé.
Les coordonnées géographiques ne sont toutefois pas idéales dans toutes les situations. Par exemple, la formule permettant de calculer la distance entre deux points dont on connaît les coordonnées géographiques n'est pas triviale.
Sachant qu'il faut de toute manière projeter la Terre pour la représenter sur une surface plane comme une carte ou un écran, il est plus simple de travailler avec les coordonnées projetées, qui sont des coordonnées cartésiennes, et c'est ce que nous ferons généralement.
Le premier type de coordonnées cartésiennes que nous utiliserons est celui utilisé pour la mensuration officielle en Suisse, décrit ci-après.
2.2. Projection suisse
La quasi-totalité des cartes représentant une partie ou l'ensemble de la Suisse — comme celle visible plus haut — sont dessinées en projetant la Terre au moyen d'une projection cartographique nommée Swiss Grid. Les paramètres de cette projection ont été choisis de manière à ce que les déformations provoquées par l'aplatissement de la sphère terrestre soient aussi petites que possibles sur le territoire suisse.
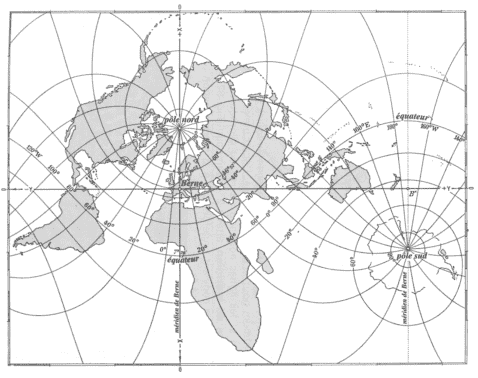
L'image ci-dessous—tirée du livre Lecture de carte de Martin Gurtner—montre l'ensemble de la Terre projetée au moyen de cette projection. Comme on le devine, la Suisse y est projetée de manière relativement fidèle, tandis que d'autres parties du monde, comme le sud de l'Afrique, y sont grossièrement déformées. La projection Swiss Grid n'est donc pas adaptée à une carte mondiale, mais convient parfaitement pour des cartes de la Suisse.
2.3. Coordonnées suisses
Une fois la Suisse projetée dans le plan au moyen de la projection Swiss Grid, il est possible d'utiliser des coordonnées cartésiennes pour désigner la position de n'importe quel point du pays.
Le système de coordonnées utilisé actuellement en Suisse se nomme CH1903+. Dans ce système, la position d'un point est donnée par deux coordonnées, qui sont :
- sa coordonnée E (est),
- sa coordonnée N (nord).
L'origine du système de coordonnées a été arbitrairement placée à Berne, et ses coordonnées ont été définies comme étant (E=2600000, N=1200000). Ces conventions sont illustrées dans la figure ci-dessous.
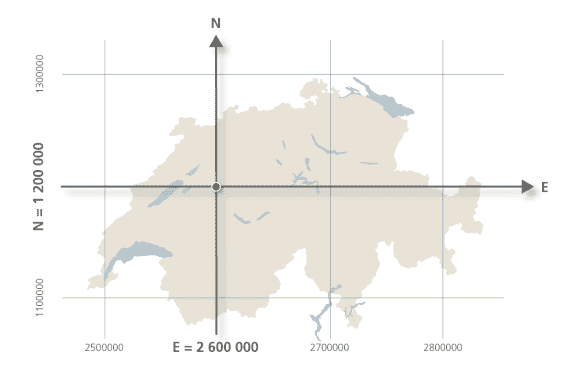
Cette définition de l'origine peut paraître surprenante, mais a l'avantage de garantir que tout point en Suisse a des coordonnées à sept chiffres exactement (avant la virgule), et que le premier chiffre de la coordonnée E vaut toujours 2, tandis que le premier chiffre de la coordonnée N vaut toujours 1. Il est donc impossible de les confondre.
Les coordonnées E et N sont données en mètres, ce qui permet d'utiliser le théorème de Pythagore pour calculer la distance en mètres entre deux points. Par exemple, la distance entre le coin sud-ouest du Learning Center (E=2533132, N= 1152206) et le sommet de la Pointe Dufour (E=2633208, N= 1087349) peut être estimée ainsi :
\[ \sqrt{\left(2\,633\,208-2\,533\,132\right)^2 + (1\,087\,349-1\,152\,206)^2} \approx 119\,254.5 \]
soit un peu moins de 120 km.
La carte interactive ci-dessous montre une fois encore la Suisse sur laquelle est cette fois superposée une grille des coordonnées suisses.
Comme on peut le voir sur cette carte en l'agrandissant, la totalité du territoire Suisse se trouve entre les coordonnées E (est) 2 485 000 et 2 834 000, et entre les coordonnées N (nord) 1 075 000 et 1 296 000. On peut en conclure que la Suisse tient dans un rectangle d'environ 349×221 kilomètres.
2.4. Conversion entre CH1903+ et WGS84
Comme expliqué plus haut, nous utiliserons généralement les coordonnées suisses dans ce projet. Toutefois, il sera parfois utile de convertir des coordonnées suisses en coordonnées WGS 84, et inversement. Pour cela, il est possible d'utiliser les formules ci-dessous, adaptées du document Formules approchées pour la transformation entre des coordonnées de projection suisses et WGS84 de swisstopo.
Pour convertir des coordonnées WGS 84 en coordonnées suisses, on peut utiliser les formules suivantes :
\begin{array}{rcrl} \lambda_1 & = && 10^{-4}\cdot\left(3\,600\cdot\lambda - 26\,782.5\right)\\[0.5em] \phi_1 & = && 10^{-4}\cdot\left(3\,600\cdot\phi - 169\,028.66\right)\\[0.5em] E & = & & 2\,600\,072.37\\ & & + & 211\,455.93 \cdot\lambda_1\\ & & - & 10\,938.51 \cdot\lambda_1\cdot\phi_1\\ & & - & 0.36\cdot\lambda_1\cdot\phi_1^2\\ & & - & 44.54\cdot\lambda_1^3\\[0.5em] N & = & & 1\,200\,147.07\\ & & + & 308\,807.95\cdot\phi_1\\ & & + & 3\,745.25\cdot\lambda_1^2\\ & & + & 76.63\cdot\phi_1^2\\ & & - & 194.56\cdot\lambda_1^2\cdot\phi_1\\ & & + & 119.79\cdot\phi_1^3 \end{array}Pour convertir des coordonnées suisses en coordonnées WGS 84, on peut utiliser les formules suivantes :
\begin{array}{rcrl} x & = & & 10^{-6}\cdot\left(E - 2\,600\,000\right)\\[0.5em] y & = & & 10^{-6}\cdot\left(N - 1\,200\,000\right)\\[0.5em] \lambda_0 & = & & 2.6779094\\ & & + & 4.728982\cdot x\\ & & + & 0.791484\cdot x\cdot y\\ & & + & 0.1306\cdot x\cdot y^2\\ & & - & 0.0436\cdot x^3\\[0.5em] \phi_0 & = & & 16.9023892\\ & & + & 3.238272\cdot y\\ & & - & 0.270978\cdot x^2\\ & & - & 0.002528\cdot y^2\\ & & - & 0.0447\cdot x^2\cdot y\\ & & - & 0.0140\cdot y^3\\ \lambda & = & & \lambda_0\cdot\frac{100}{36}\\ \phi & = & & \phi_0\cdot\frac{100}{36} \end{array}Notez que les longitudes et latitudes utilisées dans ces formules sont exprimées en degrés.
2.5. Vecteurs
L'intérêt de travailler avec des données projetées est qu'elles se trouvent dans le plan plutôt qu'à la surface d'une sphère, ce qui simplifie les calculs. Ainsi, comme nous l'avons vu plus haut, la distance entre deux points projetés peut se calculer simplement au moyen du théorème de Pythagore.
De manière plus générale, la différence entre deux points projetés peut être représentée par un vecteur à deux composantes. Ainsi, la différence entre le point \(P_2\) situé au sommet de la Pointe Dufour et le point \(P_1\) situé au coin sud-ouest du Learning Center s'exprimer sous la forme d'un vecteur \(\vec{u}\) :
\[\vec{u} = P_2 - P_1 = \begin{pmatrix} 2{}633{}208 - 2{}533{}132\\ 1{}087{}349 - 1{}152{}206 \end{pmatrix} = \begin{pmatrix} 100{}076\\ -64{}857 \end{pmatrix} \]
Bien entendu, la norme de ce vecteur, notée \(||\vec{u}||\), est égale à la distance, en mètres, séparant les deux points, calculée plus haut.
En plus du calcul de la norme, une autre opération qu'il nous sera utile d'effectuer sur les vecteurs est la projection d'un vecteur sur un autre. Comme nous le verrons dans une étape ultérieure, cette opération nous permettra de déterminer le point de l'itinéraire qui se trouve le plus proche du pointeur de la souris.
La question à laquelle nous devrons répondre sera la suivante : soient trois points, A, B (les extrémités d'un segment de l'itinéraire), et P (le pointeur de la souris), quelle est la longueur de la projection du vecteur \(\vec{u}\) allant de A à P sur le vecteur \(\vec{v}\) allant de A à B, nommée l sur la figure ci-dessous ?
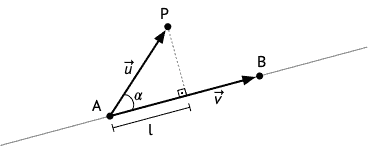
Il est facile de voir que l est donnée par :
\[ l = ||\vec{u}||\,\cos\alpha \]
et il se trouve que la partie droite de cette équation peut se récrire au moyen du produit scalaire. Pour mémoire, le produit scalaire (dot product en anglais) de deux vecteurs \(\vec{u}\) et \(\vec{v}\), noté \(\vec{u}\cdot\vec{v}\), est défini ainsi :
\[ \vec{u}\cdot\vec{v} = ||\vec{u}||\,||\vec{v}||\,\cos\alpha \]
où \(\alpha\) est l'angle entre les deux vecteurs. Ainsi, l'équation plus haut peut se récrire comme :
\begin{align} l &= ||\vec{u}||\,\cos\alpha\\ &= ||\vec{u}||\,\cos\alpha\,\frac{||\vec{v}||}{||\vec{v}||}\\ &= \frac{||\vec{u}||\,||\vec{v}||\,\cos\alpha}{||\vec{v}||}\\ &= \frac{\vec{u}\cdot\vec{v}}{||\vec{v}||} \end{align}Une propriété importante du produit scalaire est qu'il est égal à la somme des produits des composantes des vecteurs. C'est-à-dire que :
\[ \vec{u}\cdot\vec{v} = u_x v_x + u_y v_y \]
où \(u_x, u_y\) sont les composantes du vecteur \(\vec{u}\), et \(v_x, v_y\) celles du vecteur \(\vec{v}\).
Grâce à cette propriété, il est possible de récrire la formule déterminant l ainsi :
\[ l = \frac{\vec{u}\cdot\vec{v}}{||\vec{v}||} = \frac{u_x v_x + u_y v_y}{||\vec{v}||} \]
3. Mise en œuvre Java
Les concepts importants pour cette étape ayant été introduits, il est temps de décrire leur mise en œuvre en Java. En plus des classes spécifiques à cette étape, une classe « utilitaire » est à réaliser : Preconditions, qui offre une méthode de validation d'argument.
Notez que toutes les classes et interfaces de ce projet appartiendront au paquetage ch.epfl.javelo ou à l'un de ses sous-paquetages.
Attention : jusqu'à l'étape 6 du projet (incluse), vous devez suivre à la lettre les instructions qui vous sont données dans l'énoncé, et vous n'avez pas le droit d'apporter la moindre modification à l'interface publique des classes, interfaces et types énumérés décrits.
En d'autres termes, vous ne pouvez pas ajouter des classes, interfaces ou types énumérés publics à votre projet, ni ajouter des attributs ou méthodes publics aux classes, interfaces et types énumérés décrits dans l'énoncé. Vous pouvez par contre définir des méthodes et attributs privés si cela vous semble judicieux.
Cette restriction sera levée dès l'étape 7.
3.1. Installation de Java
Avant de commencer à programmer, il faut vous assurer que la version 17 de Java est bien installée sur votre ordinateur, car c'est celle qui sera utilisée pour ce projet.
Si vous n'avez pas encore installé cette version, rendez-vous sur le site Web du projet Adoptium, téléchargez le programme d'installation correspondant à votre système d'exploitation (macOS, Linux ou Windows), et exécutez-le. Ensuite, si vous utilisez Eclipse plutôt qu'IntelliJ, lisez le guide Configurer Eclipse et suivez les indications qui s'y trouvent.
3.2. Classe Preconditions
Fréquemment, les méthodes d'un programme demandent que leurs arguments satisfassent certaines conditions. Par exemple, une méthode déterminant la valeur maximale d'un tableau d'entiers exige que ce tableau contienne au moins un élément.
De telles conditions sont souvent appelées préconditions (preconditions) car elles doivent être satisfaites avant l'appel d'une méthode : c'est à l'appelant de s'assurer qu'il n'appelle la méthode qu'avec des arguments valides.
En Java, la convention veut que chaque méthode vérifie, autant que possible, ses préconditions et lève une exception — souvent IllegalArgumentException — si l'une d'entre elles n'est pas satisfaite. Par exemple, une méthode max calculant la valeur maximale d'un tableau d'entiers, et exigeant logiquement que celui-ci contienne au moins un élément, pourrait commencer ainsi :
int max(int[] array) {
if (! (array.length > 0))
throw new IllegalArgumentException();
// … reste du code
}
(Notez au passage que la méthode max ne déclare pas qu'elle lève potentiellement IllegalArgumentException au moyen d'une clause throws, car cette exception est de type unchecked.)
La première classe à réaliser dans le cadre de ce projet a pour but de faciliter l'écriture de telles préconditions. En l'utilisant, la méthode ci-dessus pourrait être simplifiée ainsi :
int max(int[] array) {
Preconditions.checkArgument(array.length > 0);
// … reste du code
}
Cette classe est nommée Preconditions et appartient au paquetage ch.epfl.javelo. Elle est publique et finale et n'offre rien d'autre que la méthode checkArgument décrite plus bas. Elle a toutefois la particularité d'avoir un constructeur par défaut privé :
public final class Preconditions {
private Preconditions() {}
// … méthodes
}
Le but de ce constructeur privé est de rendre impossible la création d'instances de la classe, puisque cela n'a clairement aucun sens — elle ne sert que de conteneur à une méthode statique. Dans la suite du projet, nous définirons plusieurs autres classes du même type, que nous appellerons dès maintenant classes non instanciables.
La méthode publique (et statique) offerte par la classe Preconditions est :
void checkArgument(boolean shouldBeTrue), qui lève l'exceptionIllegalArgumentExceptionsi son argument est faux, et ne fait rien sinon.
3.3. Classe Math2
La classe Math2, du paquetage ch.epfl.javelo, publique, finale et non instanciable, offre des méthodes statiques permettant d'effectuer certains calculs mathématiques. Elle est donc similaire à la classe Math de la bibliothèque standard Java.
En plus de son constructeur privé, cette classe offre les méthodes publiques (et statiques) suivantes :
int ceilDiv(int x, int y), qui retourne la partie entière par excès de la division dexpary, c.-à-d. \(\left\lceil x/y \right\rceil\), ou lèveIllegalArgumentExceptionsixest négatif ou siyest négatif ou nul (voir les conseils de programmation plus bas),double interpolate(double y0, double y1, double x), qui retourne la coordonnéeydu point se trouvant sur la droite passant par(0,y0)et(1,y1)et de coordonnéexdonnée (voir les conseils de programmation),int clamp(int min, int v, int max), qui limite la valeurvà l'intervalle allant deminàmax, en retournantminsivest inférieure àmin,maxsivest supérieure àmax, etvsinon ; lèveIllegalArgumentExceptionsiminest (strictement) supérieur àmax,double clamp(double min, double v, double max), qui a le même comportement que la méthode précédente mais qui prend des arguments de typedoubleplutôt queint,double asinh(double x), qui retourne le sinus hyperbolique inverse de son argumentx(voir les conseils de programmation plus bas),double dotProduct(double uX, double uY, double vX, double vY), qui retourne le produit scalaire entre le vecteur \(\vec{u}\) (de composantesuXetuY) et le vecteur \(\vec{v}\) (de composantesvXetvY),double squaredNorm(double uX, double uY), qui retourne le carré de la norme du vecteur \(\vec{u}\), c.-à-d. \(||\vec{u}||^2\),uXetuYétant les composantes de ce vecteur,double norm(double uX, double uY), qui retourne la norme du vecteur \(\vec{u}\), c.-à-d. \(||\vec{u}||\),uXetuYétant les composantes de ce vecteur,double projectionLength(double aX, double aY, double bX, double bY, double pX, double pY), qui retourne la longueur de la projection du vecteur allant du point A (de coordonnéesaXetaY) au point P (de coordonnéespXetpY) sur le vecteur allant du point A au point B (de composantesbYetbY) ; autrement dit, cette méthode retourne la valeur notée l sur la figure 4.
Notez que seules certaines de ces méthodes seront utiles dans la suite de cette étape, les autres ne le seront que dans des étapes ultérieures. Ne vous en faites donc pas si vous ne les utilisez pas immédiatement.
3.3.1. Conseils de programmation
- Méthode
ceilDiv
La partie entière par excès (ceil) d'un nombre \(n\), habituellement notée \(\left\lceil n\right\rceil\), est le plus petit entier supérieur ou égal à \(n\). Sachant que la classe
Mathde la bibliothèque Java offre la méthodeceilpermettant de calculer cette fonction, il serait techniquement possible d'écrire le corps de la méthodeceilDivainsi :return Math.ceil((double)x / (double)y);
Nous vous demandons toutefois explicitement de ne pas faire cela, car une solution plus simple existe lorsque \(x\) et \(y\) sont des entiers positifs, ce qui est le cas ici. On a alors l'équivalence suivante :
\[ \left\lceil x/y \right\rceil = \left\lfloor(x + y - 1)/y\right\rfloor \]
où \(\left\lfloor n\right\rfloor\) désigne la partie entière par défaut (floor) du nombre \(n\), c.-à-d. le plus petit entier inférieur ou égal à \(n\). Or il se trouve qu'en Java l'opérateur de division (
/) appliqué à des entiers positifs calcule justement la partie entière par défaut de la division. En d'autres termes, sixetysont des entiers positifs, alors l'expression Javax/ycalcule \(\left\lfloor x/y \right\rfloor\). Sachant cela, vous pouvez donc écrire le corps de la méthodeceilDiven utilisant uniquement une addition, une soustraction et une division entière, et c'est ce qui vous est demandé. - Méthode
interpolate
Le comportement de la méthode
interpolate, qui fait ce que l'on nomme une interpolation linéaire (linear interpolation, parfois abrégé lerp) entre deux points, peut sembler un peu obscur. La figure ci-dessous montre donc graphiquement ce que représentent ses paramètresy0,y1etx. Sa valeur de retour est simplement la coordonnéeydu point (bleu) de coordonnéexse trouvant sur la droite passant par(0,y0)et(1,y1). Notez bien quexpeut être quelconque, et n'est pas forcément compris entre 0 et 1.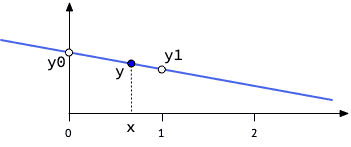
Figure 5 : Interpolation linéaire entre (0,y0)et(1,y1)La méthode
interpolateest très simple et tient en une ligne. Étant donné qu'elle détermine la position d'un point sur une droite et que l'équation d'une droite a la forme générale :\[ y = a\,x + b \]
il est clair que la méthode
interpolatedoit (entre autres) effectuer une multiplication suivie d'une addition. Notez que cela peut se faire au moyen de la méthodefma(pour fused multiply add) de la classeMath, qui calcule justement une telle séquence d'opérations, mais de manière aussi précise que possible. C'est-à-dire que l'appelfma(a,b,c)est similaire à l'expressiona*b+c, à la différence près que le résultat est plus précis car arrondi une seule fois.Nous vous conseillons donc d'utiliser la méthode
fmalorsque cela est possible. Pour la classeMath2en particulier,fmaest utile dans les définitions des méthodesinterpolateetdotProduct. - Méthode
asinh
Le sinus hyperbolique inverse peut se calculer ainsi :
\[ \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} \arsinh x = \ln\left( x + \sqrt{1 + x^2}\,\right) \]
où \(\ln\) est le logarithme naturel, fourni en Java par la méthode
logde la classeMath. Il faut noter qu'en mathématiques, le sinus hyperbolique inverse est normalement noté arsinh, alors qu'en informatique il est généralement notéasinh(sans r). C'est ce dernier nom que nous avons choisi d'utiliser pour la méthode de la classeMath2.
3.4. Classe SwissBounds
La classe SwissBounds, du paquetage ch.epfl.javelo.projection, publique, finale et non instanciable, contient des constantes et méthodes liées aux limites de la Suisse.
Ces limites sont celles données à la §2.3. Elles ne sont donc pas aussi strictes qu'elles pourraient l'être, mais cela n'a pas d'importance étant donné l'usage que nous en ferons.
La classe SwissBounds définit les constantes publiques (et bien entendu finales) suivantes :
double MIN_E, la plus petite coordonnée E de Suisse (2 485 000),double MAX_E, la plus grande coordonnée E de Suisse (2 834 000),double MIN_N, la plus petite coordonnée N de Suisse (1 075 000),double MAX_N, la plus grande coordonnée N de Suisse (1 296 000),double WIDTH, la largeur de la Suisse en mètres, définie comme la différence entreMAX_EetMIN_E,double HEIGHT, la hauteur de la Suisse en mètres, définie comme la différence entreMAX_NetMIN_N.
En plus de ces constantes, la classe SwissBounds offre une méthode, publique et statique, permettant de tester qu'un point se trouve dans les limites ci-dessus :
boolean containsEN(double e, double n), qui retourne vrai ssi (si et seulement si) les coordonnées E et N données sont dans les limites de la Suisse.
3.5. Classe Ch1903
La classe Ch1903, du paquetage ch.epfl.javelo.projection, publique, finale et non instanciable, offre des méthodes statiques permettant de convertir entre les coordonnées WGS 84 et les coordonnées suisses.
Les quatre méthodes suivantes, publiques et statiques, permettent d'effectuer les conversions :
double e(double lon, double lat), qui retourne la coordonnée E (est) du point de longitudelonet latitudelatdans le système WGS84,double n(double lon, double lat), qui retourne la coordonnée N (nord) du point de longitudelonet latitudelatdans le système WGS84,double lon(double e, double n), qui retourne la longitude dans le système WGS84 du point dont les coordonnées sonteetndans le système suisse,double lat(double e, double n), qui retourne la latitude dans le système WGS84 du point dont les coordonnées sonteetndans le système suisse.
Attention : les longitudes et latitudes que ces méthodes prennent en argument et retournent en résultat sont en radians, et pas en degrés comme dans les formules de la §2.4 ! Utilisez les méthodes toDegrees et toRadians de la classe Math pour effectuer les conversions nécessaires.
Notez que, dans un soucis de simplicité, les méthodes de Ch1903 ne valident pas leurs arguments. Au lieu de cela, la validité des coordonnées sera généralement vérifiée par les classes représentant les points, comme la classe PointCh décrite plus bas.
3.6. Enregistrements Java
Avant de décrire PointCh, la dernière classe à mettre en œuvre pour cette étape, il convient de décrire le concept de classe enregistrement (record class), ou simplement enregistrement (record). Ce type de classe a été introduit très récemment en Java, avec la version 17 du langage.
Un enregistrement est un type particulier de classe qui peut se définir au moyen d'une syntaxe plus concise qu'une classe normale. Dans cette syntaxe, le mot-clef class est remplacé par record et les attributs de la classe sont donnés entre parenthèses, après son nom.
Par exemple, un enregistrement nommé Complex représentant un nombre complexe dont les attributs sont sa partie réelle re et sa partie imaginaire im peut se définir ainsi :
public record Complex(double re, double im) { }
Cette définition est équivalente à celle d'une classe finale (!) dotée de :
- deux attributs privés et finaux nommés
reetim, - un constructeur prenant en argument la valeur de ces attributs et les initialisant,
- des méthodes d'accès (getters) publics nommés
re()etim()pour ces attributs, - une méthode
equalsretournant vrai si et seulement si l'objet qu'on lui passe est aussi une instance deComplexet que ses attributs sont égaux à ceux dethis, - une méthode
hashCodecompatible avec la méthodeequals— le but de cette méthode et la signification de sa compatibilité avecequalsseront examinés ultérieurement dans le cours, - une méthode
toStringretournant une chaîne composée du nom de la classe et du nom et de la valeur des attributs de l'instance, p. ex.Complex[re=1.0, im=2.0].
En d'autres termes, la définition plus haut, qui tient sur une ligne, est équivalente à la définition suivante, qui n'utilise que des concepts que vous connaissez déjà :
public final class Complex {
private final double re;
private final double im;
public Complex(double re, double im) {
this.re = re;
this.im = im;
}
public double re() { return re; }
public double im() { return im; }
@Override
public boolean equals(Object that) {
// … vrai ssi that :
// 1. est aussi une instance de Complex, et
// 2. ses attributs re et im sont identiques.
}
@Override
public int hashCode() {
// … code omis car peu important
}
@Override
public String toString() {
return "Complex[re=" + re + ", im=" + im + "]";
}
}
Comme cet exemple l'illustre, les enregistrements permettent d'éviter d'écrire beaucoup de code répétitif, ce que les anglophones appellent du boilerplate code. Il faut toutefois bien comprendre qu'en dehors d'une syntaxe très concise, les enregistrements n'apportent — pour l'instant en tout cas — rien de nouveau à Java, dans le sens où il est toujours possible de récrire un enregistrement en une classe Java équivalente, comme ci-dessus. En cela, les enregistrements sont similaires aux types énumérés (enums).
Il est bien entendu possible de définir des méthodes dans un enregistrement, qui viennent s'ajouter à celles définies automatiquement. Par exemple, pour doter l'enregistrement Complex d'une méthode modulus retournant son module, il suffit de l'ajouter entre les accolades, ainsi :
public record Complex(double re, double im) {
public double modulus() { return Math.hypot(re, im); }
}
(La méthode Math.hypot(x,y) retourne \(\sqrt{x^2 + y^2}\) ).
Finalement, il est aussi possible de définir ce que l'on nomme un constructeur compact (compact constructor), qui augmente le constructeur que Java ajoute par défaut aux enregistrements. Un constructeur compact doit son nom au fait qu'il semble ne prendre aucun argument, et n'initialise pas explicitement les attributs. En réalité, il prend des arguments qui sont les mêmes que ceux de l'enregistrement (re et im dans notre exemple), et Java lui ajoute automatiquement des affectations de ces arguments aux attributs correspondants.
Par exemple, on pourrait vouloir ajouter un constructeur compact à la classe Complex pour lever une exception si l'un des arguments passés au constructeur était une valeur NaN (not a number, une valeur invalide). On pourrait le faire ainsi :
public record Complex(double re, double im) {
public Complex { // constructeur compact
if (Double.isNaN(re) || Double.isNaN(im))
throw new IllegalArgumentException();
}
// … méthode modulus
}
Ce constructeur compact serait automatiquement traduit ainsi :
public final class Complex {
// … attributs re et im
public Complex(double re, double im) {
if (Double.isNaN(re) || Double.isNaN(im))
throw new IllegalArgumentException();
this.re = re; // ajouté automatiquement
this.im = im; // ajouté automatiquement
}
// … méthodes modulus, re, im, hashCode, etc.
}
Les enregistrements ne seront pas décrits en détail dans le cours, mais seront introduits au moyen d'exemples similaires à ceux ci-dessus dans la suite du projet. Les personnes intéressées par les détails de leur fonctionnement pourront se rapporter à la §8.10 (Record Classes) de la spécification du langage.
3.7. Enregistrement PointCh
L'enregistrement PointCh du paquetage ch.epfl.javelo.projection, public, représente un point dans le système de coordonnées suisse. Il est doté des attributs suivants :
double e, la coordonnée E (est) du point,double n, la coordonnée N (nord) du point.
L'enregistrement PointCh possède un constructeur compact qui lève une IllegalArgumentException si les coordonnées fournies ne sont pas dans les limites de la Suisse définies par SwissBounds. Il possède de plus les méthodes publiques suivantes :
double squaredDistanceTo(PointCh that), qui retourne le carré de la distance en mètres séparant le récepteur (this) de l'argumentthat,double distanceTo(PointCh that), qui retourne la distance en mètres séparant le récepteur (this) de l'argumentthat,double lon(), qui retourne la longitude du point, dans le système WGS84, en radians (!),double lat(), qui retourne la latitude du point, dans le système WGS84, en radians (!).
Bien entendu, la classe PointCh contient également les attributs e et n, les méthodes d'accès correspondantes, ainsi que les redéfinitions des méthodes hashCode, equals et toString que Java ajoute automatiquement aux classes enregistrements. Elles ne seront plus mentionnées à l'avenir pour de telles classes.
3.7.1. Conseils de programmation
Souvenez-vous que les coordonnées d'un point dans le système suisse sont données en mètres. Il en découle que la distance entre deux points est égale à la norme du vecteur reliant ces deux points. De même, il est évident que le carré de cette distance est égal au carré de la norme du vecteur.
3.8. Tests
Pour vous aider à démarrer ce projet, nous vous fournissons exceptionnellement une archive Zip contenant des tests unitaires JUnit pour cette étape.
Pour pouvoir utiliser ces tests, il vous faut :
3.9. Documentation
Une fois les tests exécutés avec succès, il vous reste à documenter la totalité des entités publiques (classes, attributs et méthodes) définies dans cette étape, au moyen de commentaires Javadoc, comme décrit dans le guide consacré à ce sujet. Vous pouvez écrire ces commentaires en français ou en anglais, en fonction de votre préférence, mais vous ne devez utiliser qu'une seule langue pour tout le projet.
4. Résumé
Pour cette étape, vous devez :
- installer la version 17 (et ni une plus récente, ni une plus ancienne !) de Java sur votre ordinateur, ainsi que la dernière version d'IntelliJ ou d'Eclipse,
- si vous utilisez Eclipse, le configurer selon les indications données dans le document consacré à ce sujet,
- écrire les classes
Preconditions,Math2,SwissBounds,Ch1903etPointChselon les indications ci-dessus, - vérifier que les tests que nous vous fournissons s'exécutent sans erreur, et dans le cas contraire, corriger votre code,
- documenter la totalité des entités publiques que vous avez définies,
- (optionnel mais fortement recommandé) rendre votre code au plus tard le 25 février 2022 à 17h00, via le système de rendu.
Ce premier rendu n'est pas noté, mais celui de la prochaine étape le sera. Dès lors, il est vivement conseillé de faire un rendu de test cette semaine afin de se familiariser avec la procédure à suivre.