Patrons de conception I

CS-108

1. Introduction

En programmation, comme dans toute discipline, certains problèmes sont récurrents. Un programmeur expérimenté sait identifier de tels problèmes, et connaît généralement leur solution. Il semble donc raisonnable de répertorier ces problèmes et leur solution, afin de faciliter le travail des programmeurs.

Un patron de conception (design pattern) est une solution à un problème de conception récurrent. Un tel patron est nommé et décrit en détail dans un répertoire de patrons, comme le livre Design Patterns, Elements of Reusable Object-Oriented Software de Gamma et al. qui est à l'origine de l'utilisation de cette notion en informatique.

Par exemple, la notion d'itérateur — déjà examinée dans ce cours — est un patron de conception. Elle fournit une solution au problème récurrent suivant :

Un objet possède une collection de valeurs et désire y donner accès, sans révéler la manière dont cette collection est représentée en interne.

en proposant de le résoudre ainsi :

Fournir un itérateur, à savoir un objet qui permet d'examiner les valeurs les unes après les autres, dans un ordre donné.

1.1. Avantages et inconvénients des patrons

L'intérêt des patrons de conception est qu'ils permettent de diffuser largement les meilleures solutions connues à différents problèmes récurrents. De plus, ces solutions sont nommées, ce qui permet de raisonner et de communiquer à un plus haut niveau d'abstraction que lorsqu'on se concentre sur les détails de mise en œuvre.

Cela dit, et malgré leur popularité, les patrons de conception ne sont pas une panacée. Une utilisation systématique des patrons ne saurait garantir qu'un programme soit bien conçu. Il est donc important de n'utiliser un patron que lorsque cela est justifié, et que les avantages liés à son utilisation compensent les inconvénients — p.ex. l'augmentation de la complexité du programme qui peut en résulter.

1.2. Patrons et langages de programmation

Un patron de conception décrit comment écrire et organiser un ensemble de classes pour résoudre un problème donné, et non pas un ensemble de classes concrètes. Dès lors, un patron ne peut pas être écrit une fois pour toutes et inclus dans une bibliothèque. Au lieu de cela, c'est à la personne écrivant un programme que revient la responsabilité d'appliquer le patron en écrivant les classes correspondantes. Par exemple, le concept de bâtisseur est un patron de conception — nommé Builder — qui doit être appliqué pour chaque classe pour laquelle un bâtisseur doit être fourni.

Un patron de conception n'est normalement pas lié à un langage de programmation donné. Toutefois, beaucoup d'entre eux ont été inventés dans le contexte de langages orienté-objets. Ils font une utilisation intensive des concepts de ce type de langages — classes, objets, polymorphisme d'inclusion, etc. — et sont donc difficilement utilisables tels quels dans d'autres contextes.

Il faut aussi noter que certains langages possèdent des concepts qui rendent certains patrons obsolètes.

2. Description des patrons

Un patron de conception est composé des éléments suivants :

son nom,
une description du problème résolu,
une description de la solution à ce problème,
une présentation des conséquences liées à l'utilisation du patron.

Dans le contexte des langages orienté-objets, la description de la solution consiste à expliquer comment organiser un certain nombre de classes entre elles. Il est donc utile d'avoir à disposition une manière simple de présenter de telles organisations, et nous utiliserons ici les diagrammes de classes.

2.1. Diagramme de classes

Un diagramme de classes décrit visuellement un ensemble de classes ou interfaces et leurs relations, qui peuvent être de différente nature :

héritage : lorsqu'une classe hérite d'une autre ou implémente une interface,
association : lorsqu'une classe utilise une ou plusieurs instances d'une autre classe,
instanciation : lorsqu'une classe créée des instances d'une autre classe.

Les relations d'association sont annotées avec leur nom et leur arité. Cette dernière — un entier strictement positif ou * pour indiquer une valeur arbitraire — donne le nombre d'objets liés par l'association.

Le diagramme de classes annoté ci-dessous introduit la notation utilisée au moyen d'un ensemble de classes et interfaces faisant partie d'un jeu de Monopoly.

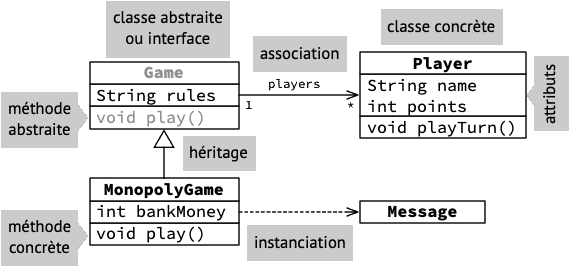
En pratique, dans cet exemple, players sera un attribut de Game, d'un type collection quelconque, p.ex. une liste.

Etant donné que les patrons décrivent une manière d'organiser un ensemble de classes — et pas un ensemble de classes réel — les diagrammes les illustrant utilisent des classes fictives signalées par des bords discontinus, dont le nom évoque généralement le rôle. Le diagramme ci-dessous est un exemple qui pourrait être utilisé dans la description du patron Builder.

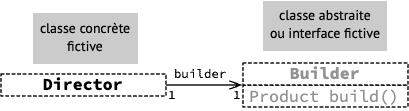
3. Le patron Builder

Pour faciliter la compréhension du concept de patron de conception, il est utile de commencer par un exemple déjà connu, ici le concept de bâtisseur (builder), et de voir comment il s'exprime sous la forme d'un tel patron.

Comme les autres patrons à venir, il sera illustré d'abord au moyen d'un exemple, puis la solution adoptée dans cet exemple sera généralisée afin d'obtenir le patron de conception en question.

3.1. Illustration du problème

Admettons que l'on désire écrire une bibliothèque de calcul matriciel. Un composant central d'une telle bibliothèque est la (ou les) classe(s) modélisant les matrices.

Comme toutes les classes représentant des entités mathématiques, ces classes devraient être immuables. Cela implique que la totalité des éléments d'une matrice doivent être spécifiés lors de sa construction. Pour les grosses matrices, ou les matrices creuses, cela peut s'avérer pénible.

Comment résoudre ce problème ?

3.2. Solution

Une solution consiste à offrir un bâtisseur de matrice, c'est-à-dire une classe représentant une matrice en cours de construction. Le bâtisseur est modifiable, et possède des méthodes pour changer les différents éléments de la matrice en cours de construction. Il possède également une méthode pour construire la matrice.

Par exemple, en admettant que les matrices soient représentées par une interface et deux classes de mise en œuvre concrètes :

public interface Matrix {
  double get(int r, int c);
  Matrix transpose();
  Matrix inverse();
  Matrix add(Matrix that);
  Matrix multiply(double that);
  Matrix multiply(Matrix that);
  // … autres méthodes
}
public final class DenseMatrix
  implements Matrix { … }
public final class SparseMatrix
  implements Matrix { … }

un bâtisseur de matrice pourrait ressembler à ceci :

public final class MatrixBuilder {
  private double[][] elements;
  public MatrixBuilder(int r, int c) {
    elements = new double[r][c];
  }
  public double get(int r, int c) {
    return elements[r][c];
  }
  public void set(int r, int c, double v) {
    elements[r][c] = v;
  }
  public Matrix build() {
    return new DenseMatrix(elements);
  }
}

Outre le fait que ce bâtisseur permet de construire une matrice en plusieurs étapes, il permet également de choisir une représentation pour la matrice qui soit appropriée à son contenu !

Par exemple, une matrice creuse — c-à-d dont la plupart des éléments valent 0 — peut être représentée au moyen d'une table associative contenant les éléments non-nuls. Une matrice dense peut être représentée par un tableau bi-dimensionnel. Le choix entre les deux représentations peut être fait par le bâtisseur au moment de la création de la matrice :

public final class MatrixBuilder {
  // … comme avant
  public Matrix build() {
    if (density() > 0.5)
      return new DenseMatrix(elements);
    else
      return new SparseMatrix(elements);
  }
}

Le diagramme de classes ci-dessous montre les classes impliquées dans la construction, par une classe Main, d'une matrice, au moyen de ce bâtisseur.

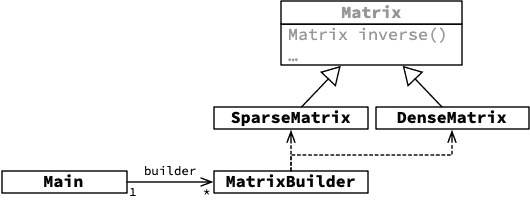
3.3. Généralisation

L'idée du bâtisseur de matrices peut être généralisée ainsi : chaque fois que le processus de construction d'une classe est assez difficile pour que l'on désire le découper en plusieurs étapes, on peut utiliser un objet pour stocker l'état de l'objet en cours de construction.

C'est l'idée du patron de conception Builder.

3.4. Diagramme de classes

Le diagramme de classes ci-dessous illustre les classes (fictives) impliquées dans la construction d'une instance de la classe Product par une instance d'une classe Director, au moyen d'un bâtisseur de classe Builder.

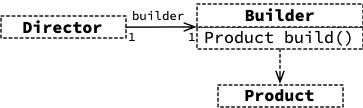
3.5. Exemple réel

La classe String (de java.lang) modélise les chaînes de caractères, qui ne sont pas modifiables.

La classe StringBuilder sert de bâtisseur pour les chaînes de caractères. Elle possède entre autres une méthode append pour ajouter la représentation textuelle d'un objet à la chaîne en cours de construction, et la méthode toString pour obtenir la chaîne construite.

4. Le patron Decorator

Le concept de patron de conception ayant rapidement été introduit au moyen d'un exemple connu, passons à deux patrons très importants en pratique et fortement liés : Decorator et Composite.

4.1. Illustration du problème

Admettons que l'on désire écrire un programme de dessin vectoriel 2D, permettant de dessiner et manipuler différentes formes géométriques. Celles-ci sont représentées par une interface Shape et plusieurs mises en œuvre, une pour chaque forme de base.

public interface Shape {
  public boolean contains(Point p);
  // … autres méthodes
}
public final class Circle implements Shape {
  …
}
// … Polygon, etc.

On désire offrir la possibilité d'appliquer différentes transformations géométriques aux formes de base : translation, rotation, symétrie, etc. Comment faire ?

Une solution consiste à définir des pseudo-formes qui en transforment d'autres. Par exemple pour la translation :

public final class Translated implements Shape {
  private final Shape shape;
  private final double dx, dy;
  public Translated(…) { … }
  public boolean contains(Point p) {
    return s.contains(new Point(p.x() - dx, p.y() - dy));
  }
  // … autres méthodes
}

Le diagramme de classes ci-dessous montre les classes impliquées dans cet exemple.

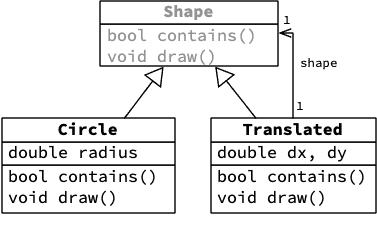
4.2. Généralisation

Chaque fois que l'on désire changer le comportement d'un objet sans changer son interface, on peut « l'emballer » dans un objet ayant la même interface mais un comportement différent. L'objet « emballant » laisse l'objet emballé faire le gros du travail, mais modifie son comportement lorsque cela est nécessaire.

Cette solution est décrite par le patron Decorator, aussi souvent appelé Wrapper.

4.3. Diagramme de classes

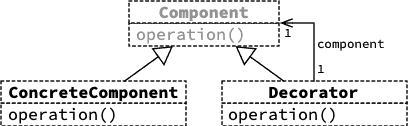
4.4. Exemples réels

Le patron Decorator se rencontre très fréquemment en pratique, comme les quelques exemples ci-dessous l'illustrent.

4.4.1. Collections Java

La bibliothèque Java offre plusieurs méthodes permettant d'obtenir des vues sur des (parties de) collections, p.ex. subList dans List, unmodifiableList dans Collections, etc. Les classes mettant en œuvre ces vues sont des décorateurs.

Cela est illustré dans le diagramme de classes ci-dessous, dans lequel on fait l'hypothèse que la méthode unmodifiableList retourne une instance d'une classe (non publique) UnmodifiableList.

4.4.2. Entrées/sorties Java

Les flots filtrants Java ne sont rien d'autre que des décorateurs de flots. Par exemple, BufferedInputStream est un décorateur ajoutant une mémoire tampon au flot sous-jacent.

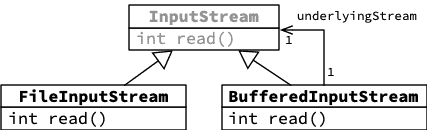
4.4.3. Interfaces graphiques

Les décorateurs sont souvent utilisés dans les bibliothèques de gestion d'interfaces graphiques pour ajouter des ornements aux éléments graphiques : bordures, barres de défilement, etc.

Le nom Decorator vient de cette utilisation.

4.5. Patron Decorator et héritage

Le patron Decorator permet de modifier le comportement d'une classe existante, tout comme l'héritage. Il est intéressant de comparer ces deux solutions sur un exemple concret. Pour ce faire, admettons que l'on désire ajouter à un ensemble HashSet la possibilité de compter le nombre total d'éléments ajoutés.

4.5.1. Solution 1 : héritage

Une première manière de procéder consiste à définir une sous-classe de HashSet redéfinissant les méthodes d'ajout add et addAll pour compter les éléments ajoutés.

public final class CountingHashSet<E> extends HashSet<E> {
  private int addCount = 0;

  @Override
  public boolean add(E e) {
    addCount += 1;
    return super.add(e);
  }
  @Override
  public boolean addAll(Collection<E> c) {
    addCount += c.size();
    return super.addAll(c);
  }
  public int addCount() { return addCount; }
}

Une fois cette classe terminée, on peut écrire un test unitaire pour vérifier son bon fonctionnement :

@Test
public void testCount() {
  CountingHashSet<Integer> s = new CountingHashSet<>();
  s.addAll(List.of(1, 2, 3, 4, 5));
  for (int i = 6; i <= 10; ++i)
    s.add(i);
  assertEquals(10, s.addCount());
}

Etonnamment, avec la version actuelle de la classe HashSet d'Oracle, ce test échoue ! En effet, addAll utilise add en interne :

boolean addAll(Collection<E> c) {
  boolean modified = false;
  for (E e : c) {
    if (add(e))
      modified = true;
  }
  return modified;
}

Mais attention :

rien ne garantit que ce soit le cas avec d'autres mises en œuvre de HashSet, et
rien ne garantit que ce sera toujours le cas à l'avenir.

En effet, le fait que addAll utilise add est un détail de mise en œuvre interne à la classe, qui ne devrait pas être visible de l'extérieur ! Ceci illustre le problème principal de l'héritage : il casse l'encapsulation. Comment peut-on faire mieux ?

4.5.2. Solution 2 : patron Decorator

Une meilleure solution consiste à appliquer le patron Decorator en définissant un décorateur d'ensemble qui compte les ajouts.

public final class CountingSet<E> implements Set<E> {
  private final Set<E> s;
  private int addCount = 0;
  public CountingSet(Set<E> s) {
    this.s = s;
  }

  @Override
  public int size() {
    return s.size();
  }

  @Override
  public boolean add(E e) {
    addCount += 1;
    return s.add(e);
  }
  // …
}

La nouvelle mise en œuvre des ensembles comptants passe le test avec succès :

@Test
public void testCount() {
  CountingSet<Integer> s =
    new CountingSet<>(new HashSet<>());
  s.addAll(List.of(1, 2, 3, 4, 5));
  for (int i = 6; i <= 10; ++i)
    s.add(i);
  assertEquals(10, s.addCount());
}

Autre avantage : ce décorateur s'applique à n'importe quel type d'ensemble, pas seulement HashSet !

Quelle est la différence cruciale entre la sous-classe et le décorateur ? La sous-classe CountingHashSet a redéfini la méthode add, et donc la méthode appelée par addAll :

boolean addAll(Collection<E> c) {
  … for (E e : c) … add(e); …
}

qui est maintenant celle de CountingHashSet. Par contre, le décorateur n'a pas redéfini la méthode add, donc l'appel dans addAll fait toujours référence à la même méthode, celle de HashSet.

4.5.3. Décorateur amélioré

Le décorateur de l'ensemble comptant fait deux choses à la fois :

il compte le nombre d'éléments ajoutés à l'ensemble,
il transmet la plupart des messages à l'ensemble décoré.

En programmation, il est toujours bien de séparer autant que possible les responsabilités (principe appelé separation of concerns en anglais). Pour ce faire, on peut séparer la mise en œuvre en deux classes :

ForwardingSet, un décorateur d'ensemble par défaut, qui ne fait rien d'autre que transmettre les messages à l'ensemble décoré.
CountingSet, qui hérite de ForwardingSet et redéfinit uniquement les méthodes add et addAll afin de compter les éléments ajoutés.

Le décorateur d'ensemble par défaut est extrêmement simple et peu intéressant :

public abstract class ForwardingSet<E> implements Set<E> {
  private Set<E> s;
  public ForwardingSet(Set<E> s) {
    this.s = s;
  }

  @Override
  public int size() { return s.size(); }

  @Override
  public boolean isEmpty() { return s.isEmpty(); }

  // …
}

Au moyen de ce décorateur d'ensemble par défaut, il devient très simple de définir le décorateur comptant :

public final class CountingSet<E> extends ForwardingSet<E>{
  private int addCount = 0;

  public CountingSet(Set<E> s) {
    super(s);
  }

  @Override
  public boolean add(E e) {
    addCount += 1;
    return super.add(e);
  }

  @Override
  public boolean addAll(Collection<E> c) {
    addCount += c.size();
    return super.addAll(c);
  }

  public int addCount() { return addCount; }
}

Comment se fait-il qu'hériter de ForwardingSet soit une bonne idée, alors qu'hériter de HashSet n'en est pas une ?

La différence cruciale est que ForwardingSet a été conçue pour servir de classe mère, ce qui n'est pas le cas de HashSet, conçue pour être utilisée comme « productrice d'objets » !

Cela se voit entre autres dans la documentation de HashSet, qui ne mentionne entre autres pas le fait que addAll utilise add en interne. Or, comme on l'a vu, cette information est cruciale pour pouvoir correctement définir une sous-classe de HashSet.

4.6. Rôle des classes

De manière générale, une classe ne peut jouer correctement qu'un seul des deux rôles suivants :

celui de créatrice d'objets,
celui de classe mère.

Malheureusement, ni Java ni les autres langages actuels ne permettent de faire clairement la différence entre ces deux rôles. De plus, par défaut toute classe peut jouer les deux rôles et c'est au programmeur d'interdire explicitement l'un ou l'autre usage, ce qu'il ne fait généralement pas.

En pratique, il est toutefois très utile de distinguer clairement deux types de classes correspondant aux rôles ci-dessus :

Une classe instanciable est une classe dont le (seul) rôle est de permettre la création d'objets. Pour empêcher son utilisation dans le rôle de classe mère, il est conseillé d'empêcher la définition de sous-classes en la déclarant finale.
Une classe héritable est une classe dont le (seul) rôle est de servir de classe mère. Pour empêcher son utilisation en tant que productrice d'objets, il est conseillé de la déclarer abstraite, même si elle ne l'est pas réellement, c-à-d même si elle ne possède pas de méthode abstraite. C'est p.ex. ce qui a été fait avec ForwardingSet.

Règle des classes : Lorsque vous écrivez une classe, décidez s'il s'agit d'une classe héritable ou instanciable. Rendez-la abstraite dans le premier cas, finale dans le second.

La documentation d'une classe héritable doit être bien plus détaillée que celle d'une classe instanciable, et décrire tous les aspects de sa mise en œuvre susceptibles d'influencer le comportement des sous-classes, p.ex. le fait qu'une méthode en utilise une autre.

Les collections Java sont un exemple réel de hiérarchie dans laquelle la distinction entre ces différents types de classes est relativement bien faite. Par exemple, la hiérarchie liée à la classe ArrayList est illustrée ci-dessous :

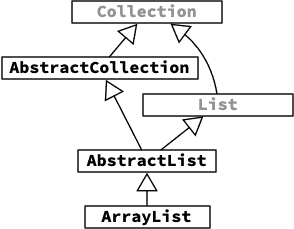
Dans cette hiérarchie, les classes AbstractCollection et AbstractList sont héritables et fournissent des mises en œuvre par défaut de la plupart des méthodes de Collection ou List. La classe ArrayList, quant à elle, est instanciable et représente la mise en œuvre des listes au moyen d'un tableau « redimensionnable ». Malheureusement, elle n'est pas finale, erreur historique qu'il est difficile de corriger actuellement pour des raisons de compatibilité.

5. Le patron Composite

5.1. Illustration du problème

On désire améliorer le programme de dessin vectoriel 2D pour offrir à l'utilisateur la possibilité de grouper plusieurs formes. Bien entendu, un groupe doit se comporter comme une forme normale, à laquelle il est possible d'appliquer des transformation, ou qu'il est possible de placer dans un groupe plus grand. Comment faire ?

Une solution consiste à définir une pseudo-forme qui représente un groupe :

public final class Group implements Shape {
  private final List<Shape> shapes;
  public Group(List<Shape> shapes) { … }
  public boolean contains(Point p) {
    for (Shape s: shapes)
      if (s.contains(p))
	return true;
    return false;
  }
  // … autres méthodes
}

Les classes impliquées dans cet exemple sont représentée dans le diagramme de classes ci-dessous :

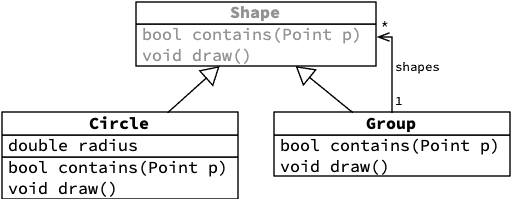
5.2. Généralisation

Lorsque les objets d'un programme peuvent être composés entre eux pour former des macro-objets, il est judicieux de faire en sorte que ceux-ci aient le même type que les objets qu'ils composent. De la sorte, il est possible de traiter les objets et les macro-objets de manière uniforme.

Cela implique entre autres que les macro-objets peuvent être composés d'autre macro-objets, de manière récursive.

Cette idée est décrite par le patron Composite.

5.3. Diagramme de classes

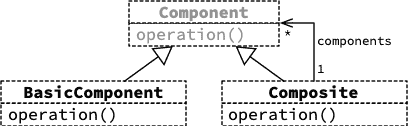
5.4. Exemples réels

5.4.1. Entrées/sorties Java

La classe SequenceInputStream prend deux flots d'entrée et produit un flot composite qui fournit d'abord les valeurs du premier puis celles du second.

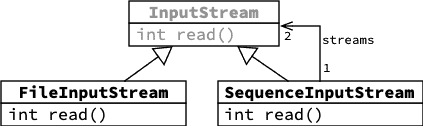
5.4.2. Interfaces graphiques

Les interfaces graphiques sont construites en combinant des composants de base — boutons, champs textuels, menus, etc.

Certains composants sont des conteneurs, c-à-d que leur rôle principal est de contenir d'autres composants. Par exemple, un panneau à onglets permet d'organiser une interface complexe en plusieurs onglets séparés.

Les composants conteneurs sont eux aussi des composants, et il est dès lors possible de placer des conteneurs dans d'autres conteneurs.

6. Composite et Decorator

La différence entre Decorator et Composite est minime et se résume au fait que le premier référence un seul objet de son propre type, le second plusieurs. Cela est visible en comparant les deux diagrammes de classes correspondant à BufferedInputStream et SequenceInputStream.

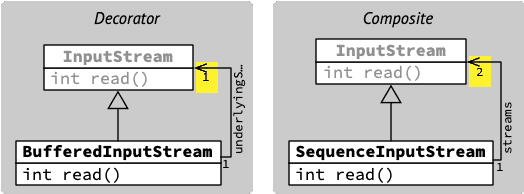
Les patrons Decorator et Composite sont très souvent utilisés ensemble pour permettre la création d'objets complexes par composition — au sens large, incluant la décoration — d'objets plus simples.

Cette approche, très puissante, est parfois qualifiée de compositionnelle ou d'algébrique. En effet, la manière dont les décorateurs et composites permettent d'obtenir de nouveaux objets à partir d'objets existants rappelle la manière dont les opérateurs algébriques — la négation, l'addition, etc. — permettent d'obtenir de nouveaux objets mathématiques à partir d'objets existants.

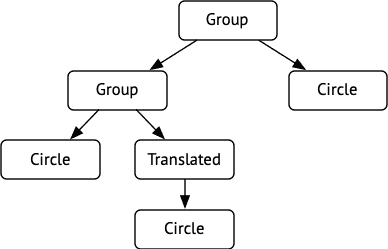
En mémoire, les objets résultant d'une telle organisation forment une structure en arbre dont les feuilles sont les objets de base et les nœuds les décorateurs — s'ils ont un seul fils — ou les composites — s'ils en ont plusieurs.

Par exemple, un dessin vectoriel pourrait ressembler à ceci :

7. Références

Design Patterns: Elements of Reusable Object-Oriented Software de Erich Gamma, Richard Helm, Ralph Johnson et John Vlissides.
Effective Java (3rd ed.) de Joshua Bloch, en particulier :
- la règle 18, Favor composition over inheritance sur les dangers de l'héritage et l'intérêt du patron Decorator,
- la règle 19, Design and document for inheritance or else prohibit it sur l'intérêt de rendre les classes instanciables finales.