État d'un joueur
tCHu – étape 4
1. Introduction
Le but principal de cette étape est d'écrire deux classes liées à la représentation de l'état d'un joueur au cours du jeu.
La première de ces classes contient toutes les informations représentant l'état d'un joueur à proprement parler — ses billets, cartes, etc. —, tandis que la seconde représente de manière efficace la connectivité de son réseau, dans le but de déterminer la valeur de ses billets.
2. Concepts
2.1. État d'un joueur
L'état d'un joueur de tCHu est constitué des informations suivantes :
- ses billets,
- ses cartes wagon/locomotive,
- les routes dont il s'est emparé,
- le nombre de wagons encore en sa possession,
- le nombre de points de construction qu'il a déjà gagné,
- le nombre de points que ses billets lui rapportent.
Il faut toutefois noter que les trois dernières informations sont redondantes et peuvent être calculées en fonction des trois autres :
- le nombre de wagons encore en possession d'un joueur est simplement égal au nombre de wagons initial (40) moins la somme de la longueur des routes dont il s'est emparé,
- le nombre de points de construction est simplement égal à la somme des points de construction de chacune de ces mêmes routes,
- le nombre de points que rapportent les billets se détermine en fonction des billets eux-même et des routes dont le joueur s'est emparé.
Certaines parties de l'état d'un joueur — les billets et cartes qu'il possède, ainsi que le nombre de points que ces billets lui rapportent — sont privées, dans le sens où l'adversaire ne doit pas les connaître avant la fin de la partie. Le reste de l'état est public et connu de l'adversaire.
2.2. Connectivité d'un réseau
Pour déterminer le nombre de points qu'un billet rapporte — ou fait perdre — à un joueur, il faut déterminer lesquels des trajets de ce billet sont réalisables avec son réseau, c-à-d les routes dont il s'est emparé. Il est donc intéressant d'avoir à disposition un moyen de déterminer, si possible rapidement, si deux gares quelconques sont reliées par le réseau d'un joueur.
Pour ce faire, on pourrait imaginer effectuer une recherche exhaustive dans le réseau du joueur pour déterminer s'il est possible d'atteindre la seconde gare à partir de la première. C'est grosso modo ce qu'un joueur humain fait.
Il existe toutefois une solution plus simple et plus efficace, qui est celle que nous allons utiliser. Elle consiste à partitionner — donc à découper en sous-ensembles disjoints — l'ensemble de toutes les gares afin de placer dans un même sous-ensemble toutes les gares reliées entre elles par le réseau du joueur.
Par exemple, imaginons qu'à un instant du jeu, le joueur 1 possède le réseau bleu figurant dans l'image ci-dessous.
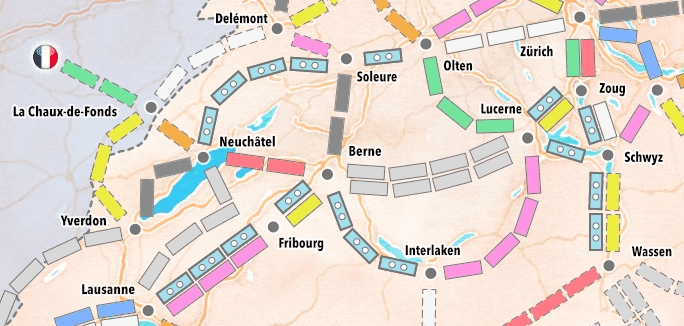
Dans ce réseau, Lausanne est par exemple connectée à Fribourg, Berne et Interlaken. Ces quatre gares appartiennent donc au même sous-ensemble de la partition. La partition des gares dont le nom est visible sur l'image ci-dessus est composée des sous-ensembles suivants (dans un ordre arbitraire) :
- { Lausanne, Fribourg, Berne, Interlaken },
- { Neuchâtel, Soleure, Olten },
- { Lucerne, Zoug, Schwyz, Wassen },
- { Delémont },
- { La Chaux-de-Fonds },
- { Yverdon },
- { Zürich }.
Une fois cette partition construite, il devient trivial de déterminer si un trajet est réalisable, puisqu'il suffit de regarder si les deux gares qu'il relie appartiennent au même sous-ensemble.
Par exemple, le trajet Lucerne - Wassen est réalisable avec le réseau ci-dessus, car les deux villes appartiennent au même sous-ensemble (le 3). Par contre, le trajet Neuchâtel - Lausanne ne l'est pas, puisque ces deux villes appartiennent à des sous-ensembles différents (le 2 et le 1 respectivement).
2.2.1. Représentation d'une partition
Ayant décidé de représenter la connectivité du réseau d'un joueur par une partition des gares, il reste encore à savoir comment représenter effectivement, par exemple en Java, une partition.
Pour ce projet, nous allons utiliser une technique connue de représentation des partitions, qui a l'avantage d'être simple, élégante et efficace. Elle consiste à choisir, pour chacun des sous-ensemble de la partition, un unique élément pour jouer le rôle de représentant (representative) du sous-ensemble. Comme son nom l'indique, cet élément représente tous les éléments du sous-ensemble auquel il appartient.
Pour notre exemple, on pourrait ainsi choisir la gare d'Interlaken comme représentant de son sous-ensemble, la gare de Neuchâtel comme représentant du sien, etc. Chaque sous-ensemble ne contenant qu'une gare n'a qu'un représentant possible, par contre pour tous les autres sous-ensembles il y en a plusieurs, et le choix exact importe peu. Seul compte le fait que chaque sous-ensemble ait exactement un représentant.
Ainsi, la partition correspondant au réseau plus haut pourrait être représentée par les sous-ensembles ci-dessous, où les représentants sont en gras :
- { Lausanne, Fribourg, Berne, Interlaken },
- { Neuchâtel, Soleure, Olten },
- { Lucerne, Zoug, Schwyz, Wassen },
- { Delémont },
- { La Chaux-de-Fonds },
- { Yverdon },
- { Zürich }.
Avec cette représentation, déterminer si un trajet entre deux gares est possible revient à déterminer si les représentants des sous-ensembles contenant les deux gares sont identiques ou non.
Par exemple, déterminer si le trajet Lucerne - Wassen est possible revient à déterminer si les représentants des sous-ensemble les contenant (ici Zoug et Zoug resp.) sont identiques, ce qui est bien le cas. De même, déterminer si le trajet Neuchâtel - Lausanne est possible revient à déterminer si les représentants des sous-ensembles les contenant (ici Neuchâtel et Interlaken resp.) sont identiques, ce qui n'est pas le cas.
Une question subsiste toutefois encore : comment obtenir facilement le représentant du sous-ensemble auquel un élément quelconque appartient ? Simplement en s'assurant que chaque élément référence le représentant du sous-ensemble auquel il appartient ! Visuellement, ces liens peuvent être représentés par des flèches allant des éléments vers le représentant de leur sous-ensemble, et notre réseau d'exemple peut donc être visualisé ainsi :
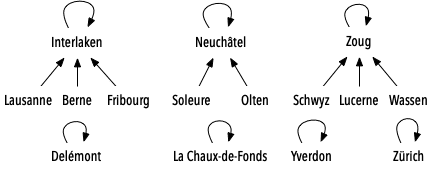
Comme cette image l'illustre, les représentants se référencent eux-mêmes, et c'est à cela qu'on les reconnaît.
2.2.2. Stockage des liens dans un tableau
La discussion ci-dessus semble indiquer que les liens allant d'un élément à son représentant — les flèches du diagramme — sont stockés dans les éléments eux-mêmes. Dans notre cas, cela signifierait que chaque gare, c-à-d chaque instance de Station, devrait contenir une référence vers la gare la représentant.
Même si une telle solution serait envisageable, elle n'est pas forcément idéale, car elle implique de stocker directement dans les gares une information qui est plutôt liée à une partition de gares qu'à la gare elle-même. De plus, une telle organisation implique qu'une gare ne peut faire partie que d'une seule partition, puisqu'elle ne peut avoir qu'une seule référence vers le représentant de son sous-ensemble.
Il est donc préférable de stocker les liens non pas de manière interne aux gares, mais de manière externe. Cela est même particulièrement simple car nous avons pris soin de numéroter toutes les gares du réseau en leur affectant à chacune une identité allant de 0 au nombre de gares moins un.
Grâce à cette identité, il est possible de représenter les liens au moyen d'un simple tableau d'entiers, contenant autant d'éléments qu'il y a de gares. À chaque position du tableau correspond donc une gare, et l'élément stocké dans chacune de ces positions est l'index du représentant du sous-ensemble auquel la gare en question appartient. Autrement dit, à chaque élément du tableau correspond une flèche de la figure ci-dessus, l'index de l'élément étant l'identité de la gare au départ de la flèche, l'élément lui-même étant l'identité de la gare à l'arrivée de la flèche.
Par exemple, admettons que les gares du réseau ci-dessus soient numérotées dans l'ordre alphabétique, ainsi :
| Gare | Id |
|---|---|
| Berne | 0 |
| Delémont | 1 |
| Fribourg | 2 |
| Interlaken | 3 |
| La Chaux-de-Fonds | 4 |
| Lausanne | 5 |
| Lucerne | 6 |
| Neuchâtel | 7 |
| Olten | 8 |
| Schwyz | 9 |
| Soleure | 10 |
| Wassen | 11 |
| Yverdon | 12 |
| Zoug | 13 |
| Zürich | 14 |
Dans ce cas, la partition présentée plus haut est représentée par le tableau d'entiers suivant :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 1 | 3 | 3 | 4 | 3 | 13 | 7 | 7 | 13 | 7 | 13 | 12 | 13 | 14 |
Grâce à ce tableau, déterminer si Lucerne (index 6) et Wassen (index 11) sont connectées revient à regarder si la valeur qui se trouve aux deux index correspondants du tableau (à savoir 13 et 13) sont identiques, ce qui est bien le cas.
2.2.3. Construction d'une partition
À ce stade, la manière dont nous représenterons les partitions de gares devrait être claire. Ce qui ne l'est toutefois pas encore est comment construire ces partitions à partir du réseau d'un joueur.
Le réseau d'un joueur n'est rien d'autre que l'ensemble des routes dont il s'est emparé. La partition des gares qui correspond peut s'obtenir en deux étapes :
- une représentation, dite profonde, de cette partition est construite,
- cette représentation profonde est aplatie afin d'obtenir celle décrite ci-dessus.
La représentation profonde d'une partition est très similaire à celle ci-dessus. La seule différence est que les éléments ne sont pas forcément liés directement au représentant de leur sous-ensemble. Au lieu de cela, ils sont liés entre eux de manière à ce que, en suivant les références, on finisse par arriver au représentant. Comme avant, celui-ci se reconnaît au fait qu'il se référence lui-même.
L'image ci-dessous montre une possibilité de représentation profonde de la partition décrite plus haut. On voit par exemple que Lausanne n'est plus liée directement au représentant de son sous-ensemble (Interlaken), mais est liée à Berne, qui est elle liée à Interlaken.
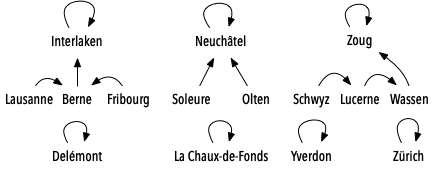
La représentation profonde a l'avantage d'être très facile à construire à partir du réseau d'un joueur. En effet, il suffit de partir d'une partition maximale des gares, c-à-d d'une partition dans laquelle chaque gare appartient à son propre sous-ensemble, qui ne contient donc qu'elle. Ensuite, les routes dont le joueur s'est emparé sont parcourues, et les sous-ensembles contenant chacune des deux gares reliées par la route sont joints.
Joindre deux sous-ensembles se fait très facilement dans la représentation profonde : il suffit de déterminer les représentants des deux sous-ensembles et d'en choisir arbitrairement un comme représentant du sous-ensemble joint. Pour ce faire, il suffit de faire en sorte que l'autre représentant le référence comme son propre représentant, et le tour est joué !
Par exemple, pour construire la représentation profonde du réseau d'exemple plus haut, on commence avec la partition maximale des gares de ce réseau, dans laquelle chaque gare est dans son propre sous-ensemble :
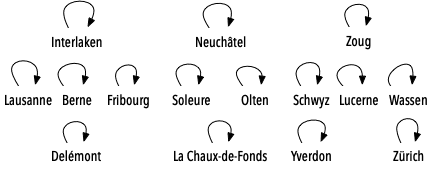
On parcourt ensuite les routes du réseau dans un ordre quelconque. Admettons que la première soit Fribourg - Berne. On modifie alors la partition afin de joindre les sous-ensembles contenant Fribourg et Berne. Pour ce faire, on cherche les représentants de ces sous-ensembles, qui sont simplement Fribourg et Berne. Ensuite, on en choisit arbitrairement un comme nouveau représentant, disons Berne, et on fait en sorte que l'autre représentant (Fribourg) le référence lui. On obtient donc la partition représentée ainsi, la référence modifiée étant indiquée par une flèche grasse :
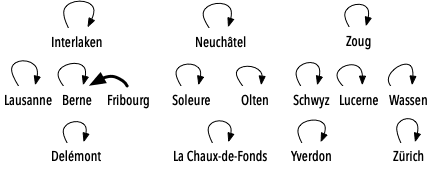
Admettons que la seconde route parcourue soit Lausanne - Fribourg. Là encore, on recherche les représentants des sous-ensembles correspondants, qui sont respectivement Lausanne et Berne. On en choisit arbitrairement un comme nouveau représentant, disons Berne, et on fait donc en sorte que l'autre (Lausanne) le référence. On obtient alors :
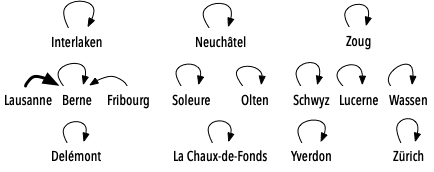
Et ainsi de suite jusqu'à ce que toutes les routes du réseau aient été parcourues, et les sous-ensembles correspondants joints.
Une fois la représentation profonde construite, il ne reste plus qu'à l'aplatir. Pour cela, il suffit de parcourir tous les éléments de la partition, de déterminer le représentant de chacun, et de lier directement l'élément à son représentant.
2.2.4. Vidéo d'exemple
La vidéo ci-dessous présente un exemple de construction et d'aplatissement d'une partition de gare, et peut être utile aux personnes auxquelles les explications ci-dessus ne suffiraient pas.
3. Mise en œuvre Java
3.1. Type énuméré PlayerId
Le type énuméré PlayerId, du paquetage ch.epfl.tchu.game, représente l'identité d'un joueur. Comme tCHu se joue à deux joueurs, ce type énuméré ne contient que deux éléments qui sont, dans l'ordre :
PLAYER_1, qui représente l'identité du joueur 1, etPLAYER_2, qui représente l'identité du joueur 2.
En plus de ces deux éléments, PlayerId offre des attributs ALL et COUNT, définis comme d'habitude, ainsi que la méthode publique suivante :
PlayerId next(), qui retourne l'identité du joueur qui suit celui auquel on l'applique, c-à-dPLAYER_2pourPLAYER_1, etPLAYER_1pourPLAYER_2.
3.2. Classe StationPartition
La classe StationPartition du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente une partition (aplatie) de gares. Elle implémente l'interface StationConnectivity, car ses instances ont pour but d'être passées à la méthode points de Ticket.
La seule méthode publique offerte par StationPartition est la mise en œuvre de la méthode connected de StationConnectivity.
En plus de cette méthode, elle offre un constructeur privé, qui prend en argument le tableau d'entiers contenant les liens liant chaque élément au représentant de leur sous-ensemble. Ce constructeur étant privé, la seule manière de construire une instance de StationPartition est d'utiliser le bâtisseur décrit à la section suivante.
Prenez garde au fait que la méthode connected doit également accepter des gares dont l'identité est hors des bornes du tableau passé à son constructeur. Lorsqu'au moins une des gares qu'on lui passe est ainsi hors bornes, elle ne retourne vrai que si les deux gares ont la même identité.
Notez que malgré la longue explication donnée à la §2.2, la classe StationPartition est triviale à écrire : le constructeur et la méthode connected s'écrivent en quelques lignes. Ne cherchez donc pas midi à quatorze heure !
3.3. Classe StationPartition.Builder
La classe Builder imbriquée statiquement dans la classe StationPartition, publique et finale, représente un bâtisseur de partition de gare. Il construit la version profonde de la partition, qu'il aplatit juste avant d'appeler le constructeur de StationPartition, dans la méthode build.
La classe Builder offre un unique constructeur public :
Builder(int stationCount), qui construit un bâtisseur de partition d'un ensemble de gares dont l'identité est comprise entre 0 (inclus) etstationCount(exclus), ou lèveIllegalArgumentExceptionsistationCountest strictement négatif (< 0).
Elle offre de plus les méthodes publiques suivantes :
Builder connect(Station s1, Station s2), qui joint les sous-ensembles contenant les deux gares passées en argument, en « élisant » l'un des deux représentants comme représentant du sous-ensemble joint ; retourne le bâtisseur (this),StationPartition build(), qui retourne la partition aplatie des gares correspondant à la partition profonde en cours de construction par ce bâtisseur.
3.3.1. Conseils de programmation
Il est fortement recommandé d'équiper le bâtisseur d'une méthode privée nommée p.ex. representative prenant en argument le numéro d'identification d'une gare et retournant celui du représentant du sous-ensemble la contenant. Une fois cette méthode définie, les méthodes connect et build sont relativement simples à écrire.
3.4. Classe PublicPlayerState
La classe PublicPlayerState du paquetage ch.epfl.tchu.game, publique et immuable, représente la partie publique de l'état d'un joueur, à savoir le nombre de billets, de cartes et de wagons qu'il possède, les routes dont il s'est emparé, et le nombre de points de construction qu'il a ainsi obtenu.
Cette classe offre un unique constructeur public :
PublicPlayerState(int ticketCount, int cardCount, List<Route> routes), qui construit l'état public d'un joueur possédant le nombre de billets et de cartes donnés, et s'étant emparé des routes données ; lèveIllegalArgumentExceptionsi le nombre de billets ou le nombre de cartes est strictement négatif (< 0).
En plus de ce constructeur, elle offre les méthodes publiques suivantes :
int ticketCount(), qui retourne le nombre de billets que possède le joueur,int cardCount(), qui retourne le nombre de cartes que possède le joueur,List<Route> routes(), qui retourne les routes dont le joueur s'est emparé,int carCount(), qui retourne le nombre de wagons que possède le joueur,int claimPoints(), qui retourne le nombre de points de construction obtenus par le joueur.
3.4.1. Conseils de programmation
Pour éviter de recalculer le nombre de wagons que possède un joueur, ou le nombre de points de construction qu'il a obtenus, stockez ces informations dans des attributs de la classe.
3.5. Classe PlayerState
La classe PlayerState du paquetage ch.epfl.tchu.game, publique, finale et immuable, représente l'état complet d'un joueur. Elle hérite de PublicPlayerState et offre un unique constructeur public :
PlayerState(SortedBag<Ticket> tickets, SortedBag<Card> cards, List<Route> routes), qui construit l'état d'un joueur possédant les billets, cartes et routes donnés.
En plus de ce constructeur public, PlayerState offre une méthode de construction statique :
PlayerState initial(SortedBag<Card> initialCards), qui retourne l'état initial d'un joueur auquel les cartes initiales données ont été distribuées ; dans cet état initial, le joueur ne possède encore aucun billet, et ne s'est emparé d'aucune route. LèveIllegalArgumentExceptionsi le nombre de cartes initiales ne vaut pas 4.
En dehors de cette méthode de construction, la classe PlayerState offre les méthodes publiques suivantes :
SortedBag<Ticket> tickets(), qui retourne les billets du joueur,PlayerState withAddedTickets(SortedBag<Ticket> newTickets), qui retourne un état identique au récepteur, si ce n'est que le joueur possède en plus les billets donnés,SortedBag<Card> cards(), qui retourne les cartes wagon/locomotive du joueur,PlayerState withAddedCard(Card card), qui retourne un état identique au récepteur, si ce n'est que le joueur possède en plus la carte donnée,PlayerState withAddedCards(SortedBag<Card> additionalCards), qui retourne un état identique au récepteur, si ce n'est que le joueur possède en plus les cartes données,boolean canClaimRoute(Route route), qui retourne vrai ssi le joueur peut s'emparer de la route donnée, c-à-d s'il lui reste assez de wagons et s'il possède les cartes nécessaires,List<SortedBag<Card>> possibleClaimCards(Route route), qui retourne la liste de tous les ensembles de cartes que le joueur pourrait utiliser pour prendre possession de la route donnée, dans le même ordre que celui utilisé par la méthodepossibleClaimCardsdeRoute, ou lèveIllegalArgumentExceptionsi le joueur n'a pas assez de wagons pour s'emparer de la route,List<SortedBag<Card>> possibleAdditionalCards(int additionalCardsCount, SortedBag<Card> initialCards, SortedBag<Card> drawnCards), qui retourne la liste de tous les ensembles de cartes que le joueur pourrait utiliser pour s'emparer d'un tunnel, trié par ordre croissant du nombre de cartes locomotives, sachant qu'il a initialement posé les cartesinitialCards, que les 3 cartes tirées du sommet de la pioche sontdrawnCards, et que ces dernières forcent le joueur à poser encoreadditionalCardsCountcartes ; lèveIllegalArgumentExceptionsi le nombre de cartes additionnelles n'est pas compris entre 1 et 3 (inclus), si l'ensemble des cartes initiales est vide ou contient plus de 2 types de cartes différents, ou si l'ensemble des cartes tirées ne contient pas exactement 3 cartes,PlayerState withClaimedRoute(Route route, SortedBag<Card> claimCards), qui retourne un état identique au récepteur, si ce n'est que le joueur s'est de plus emparé de la route donnée au moyen des cartes données,int ticketPoints(), qui retourne le nombre de points — éventuellement négatif — obtenus par le joueur grâce à ses billets,int finalPoints(), qui retourne la totalité des points obtenus par le joueur à la fin de la partie, à savoir la somme des points retournés par les méthodesclaimPointsetticketPoints.
3.5.1. Conseils de programmation
Une manière de déterminer les cartes additionnelles possibles dans la méthode possibleAdditionalCards est de procéder en trois étapes, ainsi :
- calculer le multiensemble de toutes les cartes utilisables parmi celles qui restent au joueur une fois les cartes initiales retirées de sa main — c-à-d les locomotives et les cartes de même couleur qu'une initiale,
- déterminer tous les sous-ensembles de ce multiensemble contenant le nombre de cartes additionnelles requis,
- trier cette liste de sous-ensembles par ordre croissant de nombre de cartes locomotives.
Par exemple, admettons qu'un joueur possède en main trois cartes vertes, deux bleues et deux locomotives et qu'il essaie de s'emparer d'un tunnel de couleur verte et de longueur 1 au moyen d'une de ses cartes vertes. Admettons de plus que les trois cartes tirées de la pioche impliquent l'ajout de deux cartes additionnelles. Le calcul des cartes additionnelles possibles peut se faire ainsi :
- les cartes utilisables sont au nombre de quatre : les deux vertes (le joueur en a trois en main, mais une est déjà utilisée comme carte initiale) et les deux locomotives,
- les sous-ensembles de taille 2 de ce multiensemble de taille 4 sont :
- deux vertes,
- deux locomotives,
- une verte et une locomotive,
- une fois triés par ordre croissant de nombre de cartes locomotives, ces sous-ensembles sont :
- deux vertes,
- une verte et une locomotive,
- deux locomotives.
Le calcul des sous-ensembles de la bonne taille (point 2) peut se faire au moyen de la méthode subsetsOfSize de SortedBag. Cette méthode retourne un ensemble, dont le contenu doit être placé dans une liste pour pouvoir être trié (point 3). Le tri de cette liste se fait facilement, mais comme il utilise une notion qui n'a pas encore été vue au cours — une lambda —, nous vous donnons directement le code à écrire :
List<SortedBag<Card>> options = …; // point 2 options.sort( Comparator.comparingInt(cs -> cs.countOf(Card.LOCOMOTIVE)));
Vous pouvez lire ce code de la manière suivante : la liste options doit être triée par ordre croissant (sort), en comparant (comparingInt) le nombre de locomotives (countOf(Card.LOCOMOTIVE)) de chaque élément cs.
La méthode ticketPoints doit construire la partition des gares correspondant au joueur, et pour cela doit savoir quelle valeur passer au constructeur de StationPartition.Builder. Pour cela, il lui suffit de parcourir les routes dont le joueur s'est emparé, de déterminer l'identité maximum de ces gares, et d'ajouter 1 à cette valeur.
3.6. Tests
Comme d'habitude, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.
4. Résumé
Pour cette étape, vous devez :
- écrire les classes et types énumérés
PlayerId,StationPartition,StationPartition.Builder,PublicPlayerStateetPlayerStateselon les indications données ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 19 mars 2021 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 20 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !