Modélisation du Soleil et des planètes

Le calcul de la position d'un objet céleste se fait au moyen de ce que nous appellerons un modèle de cet objet. Un modèle n'est rien d'autre qu'un ensemble d'équations mathématiques permettant de déterminer la position approximative d'un objet à un instant donné.

Tous les modèles utilisés en astronomies sont inexacts, dans le sens où il n'est pas possible de définir un modèle capable de donner la position exacte d'un objet céleste à un instant quelconque. De manière générale, plus un modèle est précis — et plus il le reste dans une plage temporelle importante —, plus il est mathématiquement complexe.

Nous avons fait le choix d'utiliser presque systématiquement les modèles les plus simples donnés dans le livre de référence pour ce projet, afin de ne pas le compliquer inutilement et éviter qu'il ne se résume à une simple traduction en Java de formules obscures. Ces modèles devraient néanmoins avoir une précision suffisante pour être utilisables lors d'observations à l'œil nu ou à la jumelle, dans une plage d'une dizaine d'années. Les groupes désirant utiliser des modèles plus précis pourront le faire dans le cadre de leur étape bonus — mais surtout pas avant !

Comme beaucoup de modèles astronomiques, ceux que nous utiliserons se basent sur la position observée de l'objet à une époque donnée, ici J2010. Ils estiment ensuite le chemin parcouru par cet objet entre l'époque et l'instant d'observation, et en déduisent sa position approximative à ce moment-là.

Beaucoup d'objets célestes parcourent une orbite elliptique autour d'un autre objet, qui se trouve dans l'un des deux foyers de l'ellipse. Par exemple, les planètes du système solaire suivent toutes des orbites elliptiques autour du Soleil, et ce dernier occupe un des foyers de l'ellipse.

Dans un tel cas, une technique souvent utilisée pour estimer la position de l'objet sur son orbite consiste à calculer dans un premier temps la position qu'il occuperait si son orbite était circulaire, puis à effectuer les corrections nécessaires pour tenir compte du fait que son orbite est en réalité elliptique. La première de ces positions est souvent appelée « moyenne », car elle est celle que l'objet occuperait s'il se déplaçait sur une orbite circulaire à une vitesse moyenne identique à sa vitesse réelle, tandis que la seconde est appelée « vraie ».

Le Soleil est l'objet céleste dont la position est la plus simple à calculer. Pour simplifier les choses, le modèle décrit plus bas fait l'hypothèse que le Soleil orbite autour de la Terre — alors que c'est en réalité l'inverse qui se produit.

La table 1 ci-dessous donne la valeur d'un certain nombre de constantes utilisées dans le calcul de la position du Soleil. Ces valeurs sont valides pour l'époque astronomique J2010 et servent de point de départ aux calculs, comme décrit plus haut. Leur signification exacte ne sera pas systématiquement décrite ici, afin d'alléger la présentation. Les personnes intéressées par les détails se reporteront au livre de référence.

Tableau 1 : Constantes solaires pour l'époque J2010

Nom	Valeur	Signification
\(\varepsilon_g\)	279.557208°	Longitude du Soleil à J2010
\(\varpi_g\)	283.112438°	Longitude du Soleil au périgée
\(e\)	0.016705	Excentricité de l'orbite Soleil/Terre

Notez que les angles donnés dans cette table et dans les suivantes sont exprimés en degrés, voir en secondes d'arc. Les formules font par contre l'hypothèse que les angles sont en radians, car c'est l'unité que nous utilisons systématiquement dans le code.

Au moyen des valeurs de la table 1, il est possible de déterminer la position approximative du Soleil en coordonnées écliptiques géocentriques — c-à-d celles utilisant le centre de la Terre comme origine — à un instant donné. Pour ce faire, on détermine successivement la valeur d'un certain nombre de variables, résumées dans la table 2 ci-dessous.

Tableau 2 : Variables utilisées dans le calcul de la position du Soleil

Nom	Unité	Signification
\(D\)	jour	Jours depuis l'époque J2010
\(M_{☉}\)	radian	Anomalie moyenne du Soleil
\(\nu_{☉}\)	radian	Anomalie vraie du Soleil
\(\lambda_{☉}\)	radian	Longitude écliptique géocentrique du Soleil
\(\phi_{☉}\)	radian	Latitude écliptique géocentrique du Soleil

La première valeur à calculer est le nombre \(D\) de jours écoulés depuis l'époque J2010 jusqu'à l'instant pour lequel on désire déterminer la position du Soleil. Une fois cette valeur connue, on peut l'utiliser pour déterminer ce que l'on nomme l'anomalie moyenne (mean anomaly) du Soleil, \(M_{☉}\), donnée par :

\[ M_{☉} = \frac{\tau}{365.242191}\times D + \varepsilon_g - \varpi_g \]

La valeur \(\tfrac{\tau}{365.242191}\) représente la vitesse angulaire moyenne de rotation de la Terre autour du Soleil, 365.242191 jours étant le temps qu'il lui faut pour effectuer un tour — durée que l'on nomme une année tropique (tropical year).

Cette anomalie moyenne peut ensuite être corrigée pour tenir compte du fait que l'orbite est en réalité elliptique, afin d'obtenir ce que l'on nomme l'anomalie vraie (true anomaly) du Soleil, \(\nu_{☉}\) :

\[ \nu_{☉} = M_{☉} + 2\,e\sin M_{☉} \]

Cela permet finalement d'obtenir la longitude écliptique du Soleil. Sa latitude écliptique vaut 0 par définition, le plan de référence étant celui de l'écliptique dans lequel se trouvent la Terre et le Soleil :

\begin{align*} \lambda_{☉} &= \nu_{☉} + \varpi_g\\ \phi_{☉} &= 0 \end{align*}

Un exemple de calcul de la position du Soleil est donné dans le livre de référence, à la §46, p. 105.

Référence : Practical Astronomy with your Calculator or Spreadsheet, §46

La taille angulaire du Soleil vu depuis la Terre varie un peu étant donné que la distance entre la Terre et le Soleil varie également — l'orbite étant elliptique et non pas circulaire. Elle peut se calculer ainsi :

\[ \theta = \theta_0\left[\frac{1 + e\,\cos\nu_{☉}}{1 - e^2}\right] \]

où \(\theta_0 = 0.533128°\).

Référence : Practical Astronomy with your Calculator or Spreadsheet, §48

Le calcul de la position des planètes est un peu plus compliqué que celui de la position du Soleil, pour deux raisons principales : premièrement, les planètes n'orbitent pas dans le plan de l'écliptique, mais dans un plan qui leur est propre ; et deuxièmement, nous désirons déterminer la position de la planète en coordonnées écliptiques géocentriques, et il faut donc connaître à la fois la position de la planète et celle de la Terre.

La stratégie de calcul consiste donc à procéder en quatre étapes :

1. la position de la planète sur sa propre orbite est déterminée selon un principe similaire à celui utilisé pour le Soleil,
2. la position de la planète est projetée sur le plan de l'écliptique puis exprimée en coordonnées écliptiques héliocentriques, c-à-d dans un repère utilisant le centre du Soleil comme origine,
3. la position de la Terre est déterminée dans ce même repère,
4. la position de la Terre et de la planète sont combinées pour obtenir la position de cette dernière en coordonnées écliptiques géocentriques.

Tout comme pour le Soleil, un certain nombre de constantes sont nécessaires aux calculs. Elles sont données dans les tables 4 et 5 plus bas, et le nom et une brève description de chacune d'entre elles apparaît dans la table 3. Le contenu de ces tables provient du livre de référence (table 8, p. 123).

L'abréviation UA signifie unité astronomique (astronomical unit, AU en anglais), qui est une … unité astronomique de distance, qui correspond à la distance moyenne entre le Soleil et la Terre.

Tableau 3 : Constantes planétaires

Nom	Unité	Signification
\(T_p\)	année tropique	Période de révolution
\(\varepsilon\)	degré/radian	Longitude à J2010
\(\varpi\)	degré/radian	Longitude au périgée
\(e\)	—	Excentricité de l'orbite
\(a\)	UA	Demi grand-axe de l'orbite
\(i\)	degré/radian	Inclinaison de l'orbite à l'écliptique
\(\Omega\) 1	degré/radian	Longitude du nœud ascendant

La table 4 ci-dessous donne la valeur des quatre premières constantes pour les planètes du système solaire.

Tableau 4 : Constantes planétaires pour l'époque J2010, partie 1

Planète	\(T_p\)	\(\varepsilon\)	\(\varpi\)	\(e\)
Mercure	0.24085	75.5671	77.612	0.205627
Vénus	0.615207	272.30044	131.54	0.006812
Terre	0.999996	99.556772	103.2055	0.016671
Mars	1.880765	109.09646	336.217	0.093348
Jupiter	11.857911	337.917132	14.6633	0.048907
Saturne	29.310579	172.398316	89.567	0.053853
Uranus	84.039492	271.063148	172.884833	0.046321
Neptune	165.84539	326.895127	23.07	0.010483

La table 5 ci-dessous donne la valeur des trois dernières constantes pour ces mêmes planètes.

Tableau 5 : Constantes planétaires pour l'époque J2010, partie 2

Planète	\(a\)	\(i\)	\(\Omega\)
Mercure	0.387098	7.0051	48.449
Vénus	0.723329	3.3947	76.769
Terre	0.999985	—	—
Mars	1.523689	1.8497	49.632
Jupiter	5.20278	1.3035	100.595
Saturne	9.51134	2.4873	113.752
Uranus	19.21814	0.773059	73.926961
Neptune	30.1985	1.7673	131.879

Ces constantes étant connues, il est possible de procéder aux calculs. La table 6 ci-dessous résume les différentes variables utilisées dans ces calculs.

Tableau 6 : Variables utilisées dans le calcul de la position des planètes

Nom	Unité	Signification
\(D\)	jour	Jours depuis J2010
\(M\)	radian	Anomalie moyenne
\(\nu\)	radian	Anomalie vraie
\(r\)	UA	Rayon (distance au Soleil)
\(l\)	radian	Longitude héliocentrique
\(r^\prime\)	UA	Projection du rayon sur l'écliptique
\(l^\prime\)	radian	Longitude écliptique héliocentrique
\(\psi\)	radian	Latitude écliptique héliocentrique
\(\lambda\)	radian	Longitude écliptique (géocentrique)
\(\beta\)	radian	Latitude écliptique (géocentrique)

Tout comme pour le Soleil, on commence par déterminer l'anomalie moyenne puis l'anomalie vraie :

\begin{align*} M &= \frac{\tau}{365.242191}\times\frac{D}{T_p} + \varepsilon - \varpi\\[0.5em] \nu &= M + 2\,e\sin M \end{align*}

On en détermine le rayon et la longitude de la planète dans le plan de son orbite, ainsi que sa latitude écliptique héliocentrique :

\begin{align*} r &= \frac{a\left(1 - e^2\right)}{1 + e\cos\nu}\\[0.5em] l &= \nu + \varpi\\[0.5em] \psi &= \arcsin\left[\sin(l - \Omega)\,\sin i\right] \end{align*}

Le rayon et la longitude sont ensuite projetés sur le plan de l'écliptique :

\begin{align*} r^\prime &= r\cos\psi\\[0.5em] l^\prime &= \arctan\left[\frac{\sin\left(l - \Omega\right)\cos i}{\cos\left(l - \Omega\right)}\right] + \Omega \end{align*}

Une fois l'ensemble de ces valeurs déterminé, on peut les utiliser pour calculer les coordonnées écliptiques géocentriques de la planète. Il faut toutefois distinguer deux cas : celui des planètes orbitant plus près du Soleil que la Terre, et celui des planètes orbitant plus loin.

Pour déterminer la taille angulaire d'une planète, on divise simplement sa taille angulaire à une distance de 1 UA, \(\theta_0\), par la distance qui la sépare de la Terre, \(\rho\) :

\[ \theta = \frac{\theta_0}{\rho} \]

La table ci-dessous donne la taille angulaire des planètes — Terre exceptée — à une distance de 1 UA, exprimée en secondes d'arc (!).

Tableau 7 : Taille angulaire des planètes à 1 UA

	Mercure	Vénus	Mars	Jupiter	Saturne	Uranus	Neptune
\(\theta_0\)	6.74	16.92	9.36	196.74	165.60	65.80	62.20

La distance séparant une planète de la Terre se calcule quant à elle grâce à l'équation suivante :

\[ \rho^2 = R^2 + r^2 - 2\,R\,r \cos\left(l - L\right)\cos\psi \]

dans laquelle toutes les distances sont exprimées en UA.

Référence : Practical Astronomy with your Calculator or Spreadsheet, §57

La magnitude d'une planète peut s'estimer en calculant tout d'abord sa phase \(F\) qui, pour mémoire, est la portion illuminée de son disque tel qu'on le voit depuis la Terre :

\[ F = \frac{1 + \cos\left(\lambda - l\right)}{2} \]

Une fois la phase connue, on peut obtenir une approximation de sa magnitude \(m\) au moyen de la formule suivante :

\[ m = V_0 + 5\log_{10}\left(\frac{r\,\rho}{\sqrt{F}}\right) \]

où \(V_0\) est la magnitude de la planète vue d'une distance de 1 UA. Les valeurs de cette constante pour les différentes planètes du système solaire sont données dans la table suivante :

Tableau 8 : Magnitude des planètes à 1 UA

	Mercure	Vénus	Mars	Jupiter	Saturne	Uranus	Neptune
\(V_0\)	-0.42	-4.40	-1.52	-9.40	-8.88	-7.19	-6.87

Référence : Practical Astronomy with your Calculator or Spreadsheet, §58 et §60

Même à l'œil nu, plusieurs milliers d'étoiles sont visibles depuis la Terre, et l'utilisation d'instruments d'observation — jumelles, lunettes ou télescopes — augmente grandement ce nombre. La question de savoir comment les désigner se pose donc.

Les étoiles les plus brillantes ont généralement un nom commun — p.ex. Rigel, Bételgeuse ou Bellatrix, toutes trois dans la constellation d'Orion —, mais les étoiles les moins brillante n'en ont pas.

Pour résoudre ce problème, de nombreux projets, individuels ou collectifs, ont eu pour but de cataloguer un aussi grand nombre d'étoiles que possible, et de leur donner ainsi une identité.

Par exemple, au début du quinzième siècle, l'astronome Johann Bayer a établi le premier atlas précis du ciel. Dans cet atlas, chaque étoile est nommée au moyen d'une lettre grecque suivie du nom latin de la constellation à laquelle elle appartient. Ainsi, dans l'atlas de Bayer, Rigel se nomme β Orionis.

Plus récemment, au début des années 1990, le projet Hipparcos de l'Agence Spatiale Européenne a tenté de répertorier et de mesurer les caractéristiques principales d'un aussi grand nombre d'étoiles que possible. Un résultat de ce projet est le catalogue Hipparcos, qui décrit un très grand nombre d'étoiles et leur attribue un numéro d'identification unique. Ainsi, Rigel y porte le numéro d'identification (HIP) 24436.

Une caractéristique des étoiles est qu'elles ont toutes une couleur qui, dans de bonnes conditions d'observation, est perceptible à l'œil nu. Ainsi, Rigel est bleutée, tandis que Bételgeuse est rougeâtre.

Cette couleur est due à certaines caractéristiques physiques de chaque étoile. En astronomie, elle est décrite par l'indice de couleur B-V (B-V color index). Sans rentrer dans les détails, une étoile dont l'indice est petit est plutôt bleue, tandis qu'une étoile dont l'indice est grand est plutôt rouge. Ainsi, l'indice de couleur de Rigel est d'environ –0.03, tandis que celui de Bételgeuse est d'environ 1.50.

A partir de cet indice, il est possible de déterminer approximativement la température de couleur (color temperature) \(T\) de l'étoile, au moyen de la formule suivante, où \(c\) est l'indice de couleur :

\[ T = 4600 \left[\frac{1}{0.92\,c + 1.7} + \frac{1}{0.92\,c + 0.62} \right]\]

Cette température de couleur, exprimée en degrés Kelvin, correspond à la température de ce que l'on appelle un corps noir (black body), qui est un objet émettant de la lumière uniquement en raison de la température à laquelle il se trouve.

La température de couleur est souvent utilisée pour décrire la couleur de la lumière émise par une source lumineuse, p.ex. une ampoule. La correspondance entre température de couleur et couleur effective est illustrée par l'image ci-dessous.

Ainsi, en appliquant la formule ci-dessus à l'indice de couleur de Rigel, on obtient une température d'environ 10500°K, tandis qu'on obtient environ 3800°K pour Bételgeuse. En consultant l'image ci-dessus pour ces deux températures, on constate qu'elles correspondent bien au fait que Rigel est plutôt bleue, Bételgeuse plutôt rouge.

On appelle astérisme (asterism) une figure dessinée par un groupe d'étoiles particulièrement brillantes. Dans le langage courant, on les désigne souvent par le terme de constellation, même si cela n'est pas strictement correct.

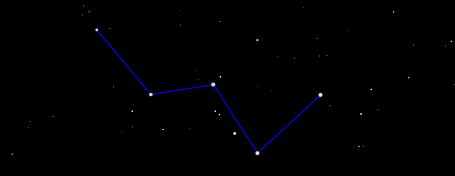
Sur les cartes du ciel, les astérismes sont souvent représentés en reliant les étoiles qui les constituent par des segments de droites, qui constituent une aide précieuse à l'observation. Par exemple, l'image ci-dessous montre un astérisme bien connu, le « W » formé par cinq étoiles de la constellation de Cassiopée.

La classe Star du paquetage ….astronomy, publique, finale et immuable, représente une étoile. Elle hérite de CelestialObject car, dans le cadre de ce projet en tout cas, les étoiles sont fixes dans le repère équatorial et n'ont donc pas de modèle associé.

La classe Star offre un constructeur public :

• Star(int hipparcosId, String name, EquatorialCoordinates equatorialPos, float magnitude, float colorIndex), qui construit une étoile avec le numéro Hipparcos, le nom, la position équatoriale, la magnitude et l'indice de couleur donnés ; lève IllegalArgumentException si le numéro Hipparcos est négatif, ou si l'indice de couleur n'est pas compris dans l'intervalle [-0.5, 5.5].

Ce constructeur doit passer 0 comme taille angulaire au constructeur de CelestialObject, car les étoiles sont tellement distantes de la Terre qu'elles sont perçues comme de simples points.

En plus de ce constructeur, la classe Star offre deux méthodes d'accès publiques, qui sont :

• int hipparcosId(), qui retourne le numéro Hipparcos de l'étoile,
• int colorTemperature(), qui retourne la température de couleur de l'étoile, en degrés Kelvin, arrondie par défaut (c-à-d à l'entier inférieur le plus proche).

La classe Asterism du paquetage ….astronomy, publique, finale et immuable, représente un astérisme.

Dans le cadre de ce projet, un astérisme n'est rien d'autre qu'une liste d'étoiles, et cette classe est donc presque triviale, ne contenant qu'un constructeur :

• Asterism(List<Star> stars), qui construit un astérisme composé de la liste d'étoiles données, ou lève IllegalArgumentException si celle-ci est vide,

et une méthode d'accès permettant d'obtenir la liste d'étoiles :

• List<Star> stars(), qui retourne la liste des étoiles formant l'astérisme.

L'interface CelestialObjectModel du paquetage ….astronomy, publique, représente un modèle d'objet céleste, c-à-d une manière de calculer les caractéristiques de cet objet à un instant donné.

Cette interface est générique, et son paramètre de type O représente le type des objets modélisés par le modèle. Elle ne possède qu'une seule méthode, publique et abstraite :

• O at(double daysSinceJ2010, EclipticToEquatorialConversion eclipticToEquatorialConversion), qui retourne l'objet modélisé par le modèle pour le nombre (éventuellement négatif) de jours après l'époque J2010 donné, en utilisant la conversion donnée pour obtenir ses coordonnées équatoriales à partir de ses coordonnées écliptiques.

Le type énuméré SunModel du paquetage ….astronomy, public et immuable, contient un seul élément nommé SUN et représentant un modèle du Soleil. Ce type énuméré implémente l'interface CelestialObjectModel<Sun>.

Il peut sembler étrange de définir un type énuméré pour le modèle du Soleil, sachant qu'il n'en existe qu'un : à quoi bon utiliser un type énuméré pour un unique objet ?

L'avantage de cette solution est qu'elle nous simplifie les choses, car les membres d'un type énuméré possèdent automatiquement plusieurs caractéristiques désirables pour le modèle du Soleil. Ainsi, Java garantit qu'il n'existe qu'une seule instance du modèle, lui ajoute une méthode toString utile, etc.

La seule méthode publique de SunModel est la méthode at de l'interface CelestialObjectModel.

Le type énuméré PlanetModel du paquetage ….astronomy, public et immuable, contient les modèles des huit planètes du système solaire. Il implémente l'interface CelestialObjectModel<Planet>. Ses éléments sont nommés, dans l'ordre, MERCURY, VENUS, EARTH, MARS, JUPITER, SATURN, URANUS et NEPTUNE.

Ce type énuméré possède un constructeur — qui, pour mémoire, ne peut être ni public ni protégé pour un type énuméré — prenant en arguments le nom français de la planète suivi des paramètres suivants, dans l'ordre :

• les 4 paramètres de la table 4,
• les 3 paramètres de la table 5,
• la taille angulaire à 1 UA provenant de la table 7,
• la magnitude à 1 UA provenant de la table 8.

Attention : ces paramètres doivent être acceptés dans les mêmes unités que celles utilisées dans ces tables, mais les angles doivent tous être convertis en radians avant d'être stockés ou utilisés, conformément à la convention utilisée dans ce projet.

Pour vous éviter une fastidieuse copie des tables données plus haut, nous vous fournissons ci-dessous la définition des 8 membres du type énuméré, que vous pouvez simplement copier dans votre projet.

MERCURY("Mercure", 0.24085, 75.5671, 77.612, 0.205627, 0.387098, 7.0051, 48.449, 6.74, -0.42), VENUS("Vénus", 0.615207, 272.30044, 131.54, 0.006812, 0.723329, 3.3947, 76.769, 16.92, -4.40), EARTH("Terre", 0.999996, 99.556772, 103.2055, 0.016671, 0.999985, 0, 0, 0, 0), MARS("Mars", 1.880765, 109.09646, 336.217, 0.093348, 1.523689, 1.8497, 49.632, 9.36, -1.52), JUPITER("Jupiter", 11.857911, 337.917132, 14.6633, 0.048907, 5.20278, 1.3035, 100.595, 196.74, -9.40), SATURN("Saturne", 29.310579, 172.398316, 89.567, 0.053853, 9.51134, 2.4873, 113.752, 165.60, -8.88), URANUS("Uranus", 84.039492, 271.063148, 172.884833, 0.046321, 19.21814, 0.773059, 73.926961, 65.80, -7.19), NEPTUNE("Neptune", 165.84539, 326.895127, 23.07, 0.010483, 30.1985, 1.7673, 131.879, 62.20, -6.87);

PlanetModel offre un attribut public et statique nommé ALL, de type List<PlanetModel> et contenant une liste immuable constituée des huit modèles de planètes, dans leur ordre de déclaration (MERCURY, VENUS, etc.).

La seule méthode publique offerte par PlanetModel est la méthode at de l'interface CelestialObjectModel.

Comme d'habitude, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.

Pour écrire vos tests, nous vous conseillons une fois encore de vous reporter au livre de référence, Practical Astronomy with your Calculator or Spreadsheet. Lisez néanmoins ce qui suit avant de vous baser sur les valeurs qui s'y trouvent.

Il semble que le livre utilise une conversion entre les coordonnées écliptique et les coordonnées équatoriales différente de la nôtre, et les valeurs obtenues après conversion sont donc légèrement différentes.

Nous vous conseillons donc soit de faire vos tests sur les coordonnées écliptiques — ce qui impose d'exposer à vos tests une méthode package-private les calculant —, soit de prendre les coordonnées écliptiques données dans le livre, les convertir avec votre conversion (supposée correcte) en coordonnées équatoriales, puis de comparer celles-ci avec les coordonnées que vous obtenez.