Conversions de coordonnées
Rigel – étape 3
1 Introduction
Le but principal de cette troisième étape est d'écrire les classes permettant de faire deux types de conversion de coordonnées :
- des coordonnées écliptiques aux coordonnées équatoriales,
- des coordonnées équatoriales aux coordonnées horizontales.
Pour pouvoir les faire, il faut toutefois connaître quelques concepts liés au temps, qui sont introduits ci-dessous.
2 Concepts
2.1 Époque astronomique
En astronomie, la stratégie couramment utilisée pour prédire la position d'un objet, p.ex. la Terre, à un instant d'observation donné, consiste à :
- consulter un ouvrage de référence astronomique pour connaître la position de l'objet, la Terre dans notre exemple, à un instant de référence choisi par les éditeurs de l'ouvrage, qui pourrait p.ex. être le 1er janvier 2000 à 12h00 UTC,
- calculer le temps écoulé entre l'instant de référence et l'instant d'observation,
- estimer, au moyen d'un modèle du mouvement de la Terre et du temps écoulé depuis l'instant de référence, la position à l'instant d'observation.
L'instant de référence utilisé, qui est un simple couple date/heure, est appelé l'époque (epoch en anglais).
En général, afin d'éviter les confusions, les astronomes essaient de ne pas multiplier les époques utilisées, mais de se limiter à un petit nombre d'époques standard. Dans le cadre de ce projet, nous en utiliserons deux, nommées J2000 et J2010 et définies ainsi :
- J2000
- le 1er janvier 2000 à 12h00 UTC,
- J2010
- le 31 décembre 2009 (!) à 0h00 UTC (que l'on peut aussi voir comme le 0 janvier 2010 à 0h00 UTC, d'où le nom donné à cette époque).
Le sigle UTC désigne le fuseau horaire utilisé, qui est celui de l'Angleterre en dehors des périodes durant lesquelles l'heure d'été est en vigueur. Pour les besoins de ce projet, on peut considérer ce fuseau comme équivalent à l'ancien GMT (pour Greenwich Mean Time).
J2000 est une époque utilisée très fréquemment en astronomie, tandis que J2010 a été choisie par les auteurs du livre de référence que nous utilisons. La quasi-totalité des formules de ce livre se basent donc sur J2010.
La raison pour laquelle J2010 est définie au moyen de la date du 0 janvier 2010 est que cela facilite quelque peu le calcul du nombre de jours écoulés depuis cette date jusqu'à une date quelconque. Cela n'aura pas vraiment d'importance pour ce projet, car la bibliothèque Java se chargera de tous les calculs liés au temps, mais il faut néanmoins que nous utilisions la définition correcte de cette époque.
2.2 Temps solaire
La durée d'un jour civil — 24 heures — a été définie en fonction du Soleil, dans le sens où un jour est le temps qu'il faut, en moyenne, pour que le Soleil se retrouve au même azimut dans le ciel. L'instant auquel un jour commence — minuit — a quant à lui été initialement défini afin que le Soleil soit, en moyenne, plein sud (azimut 180°) à midi.
Cette seconde définition a pour caractéristique d'être locale, dans le sens où l'instant auquel un jour commence n'est pas le même pour tous les endroits de la Terre, car il dépend de la longitude de l'endroit. Par exemple, le Soleil se trouve plein sud à Zürich environ 8 minutes avant qu'il ne soit plein sud à Lausanne, en raison des 2° de longitude séparant ces villes.
A l'époque où les gens ne se déplaçaient que rarement et lentement, le fait que les différentes villes d'un pays soient toutes à des heures différentes n'était pas bien gênant. Toutefois, avec l'apparition de moyens de transport et de communication de plus en plus rapides, et d'horloges de plus en plus précises, la situation est devenue intenable. Pour résoudre (partiellement) le problème, la notion de fuseau horaire a été introduite, réduisant ainsi le nombre d'heures différentes en usage, et permettant à la plupart des pays de n'utiliser qu'une seule heure sur tout leur territoire. La carte ci-dessous montre les fuseaux horaires actuels, et peut être agrandie d'un clic.
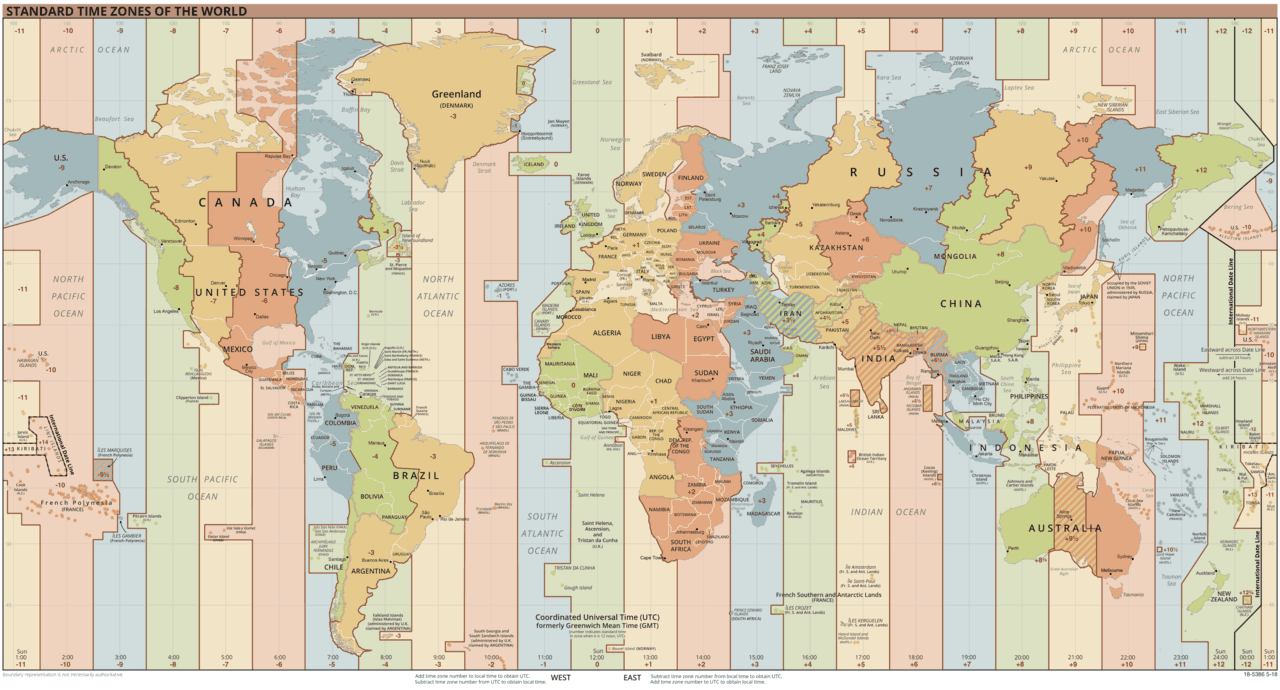
L'existence des fuseaux horaires implique qu'en la plupart des endroits de la Terre il existe une différence, plus ou moins importante, entre le temps solaire — pour lequel le Soleil est plein sud à midi — et le temps officiel. La carte ci-dessous illustre ces différences pour tous les points du monde.
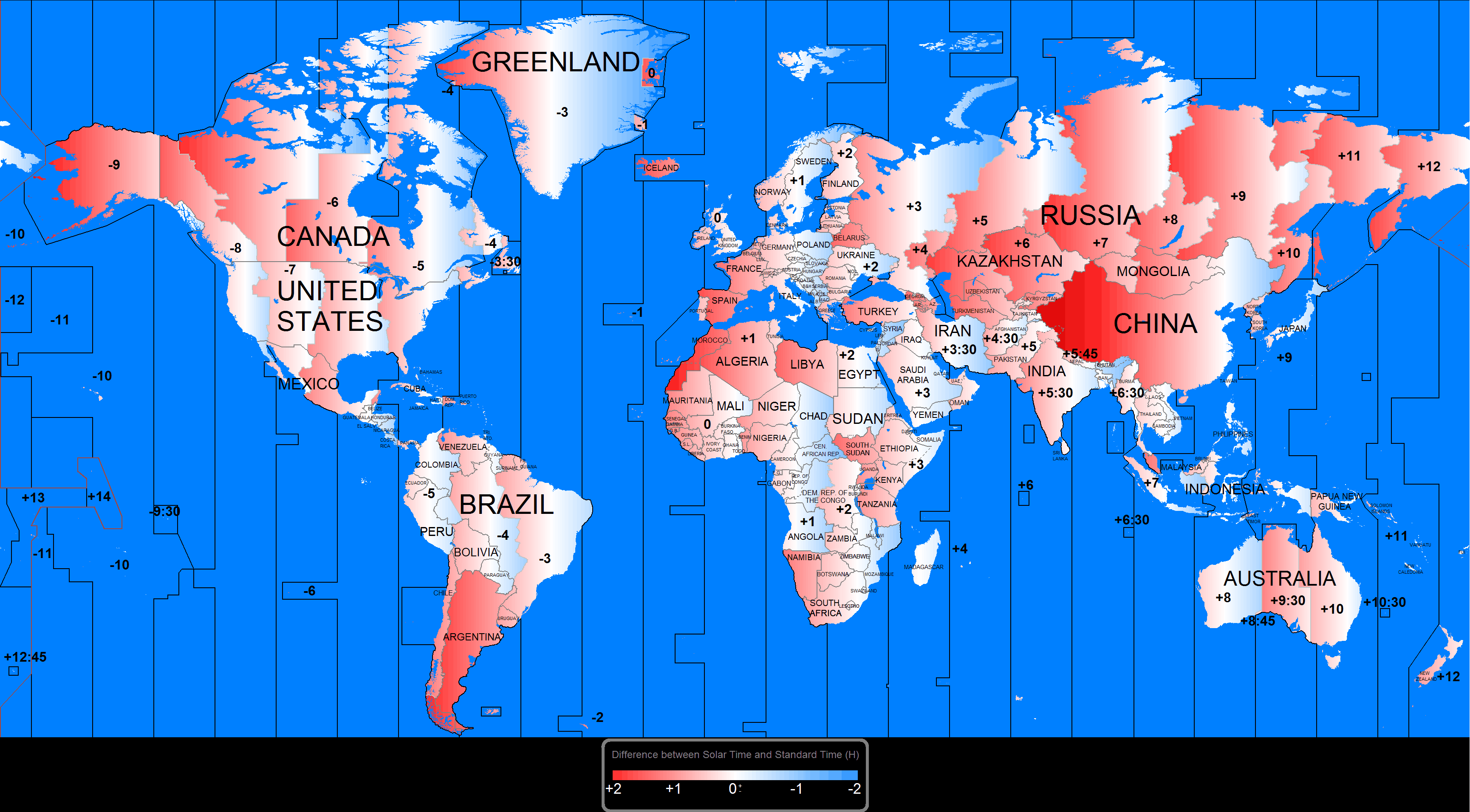
2.3 Temps sidéral
On pourrait penser que le temps qu'il faut au Soleil pour se retrouver au même azimut d'un point — qui définit la durée du jour civil — est égal au temps qu'il faut à la Terre pour faire un tour sur elle-même. Or ce n'est pas le cas, car la Terre orbite autour du Soleil en même temps qu'elle tourne sur elle-même, dans ce qu'on appelle un mouvement prograde.
Ainsi, lorsque la Terre fait un tour sur elle-même, elle avance également sur son orbite, comme illustré à la figure 3 ci-dessous. En conséquence, après avoir fait exactement un tour sur elle-même entre les points 1 et 2, elle a également changé de position par rapport au Soleil. Pour que le Soleil se retrouve à la même position dans le ciel d'un observateur situé sur la Terre, il faut donc que celle-ci continue à tourner sur elle-même durant un certain temps et atteigne point 3.
On nomme le temps qu'il faut à la Terre pour faire un tour sur elle-même le jour sidéral (sidereal day). Sa durée est d'environ 23h 56m 04s, et les 3m 56s qui manquent pour obtenir 24h correspondent au temps qu'il faut à la Terre pour passer du point 2 au point 3 dans la figure ci-dessus.
Le jour sidéral est une notion importante en astronomie, car après que la Terre ait fait un tour sur elle-même, toutes les étoiles se retrouvent aux mêmes positions dans le ciel. Par exemple, depuis l'EPFL, Rigel se trouvera à l'azimut 180° (plein sud) et à l'altitude 35.32° le 24 février 2020 à 19h 32m 33s. Dès lors, elle se retrouvera exactement à la même position un jour sidéral plus tard, c-à-d le 25 février 2020 à 19h 28m 37s.
Tout comme avec le temps solaire, il est possible de définir une origine pour le temps sidéral, c-à-d de choisir un moment auquel un jour sidéral commence. La convention retenue par les astronomes est qu'un jour sidéral commence en un endroit donné lorsque le point vernal est plein sud (azimut 180°). Pour mémoire, le point vernal est à l'intersection des plans de l'équateur et de l'écliptique, et sert d'origine à la longitude des coordonnées équatoriales (c-à-d l'ascension droite) et écliptiques (c-à-d la longitude écliptique).
Il est clair que le temps sidéral est un temps local, dans le sens où il dépend de la longitude à laquelle on se trouve sur Terre, exactement comme le temps solaire avant l'introduction des fuseaux horaires. Il n'existe par contre pas d'équivalent aux fuseaux horaires pour le temps sidéral, son usage étant limité aux calculs astronomiques.
2.4 Angle horaire
Comme rappelé ci-dessus, le point vernal sert d'origine à l'ascension droite, la coordonnée correspondant à la longitude dans le système équatorial. Or le point vernal est aussi utilisé pour définir l'origine du temps sidéral, puisque celui-ci vaut 0 quand le point vernal est plein sud.
En conséquence de cela — et du fait que l'ascension droite croît vers l'est, ce qui n'a pas été mentionné précédemment —, un objet astronomique se trouve plein sud lorsque le temps sidéral est égal à son ascension droite ! C'est d'ailleurs la raison pour laquelle l'ascension droite est généralement mesurée en heures plutôt qu'en degrés, ce qui la rend aisément comparable au temps sidéral.
Il peut paraître étrange de comparer le temps sidéral — dont le nom semble indiquer qu'il s'agit d'une unité de temps — et l'ascension droite — un angle. Mais il faut se souvenir que le temps sidéral est lié à la rotation de la Terre. Par définition, la Terre fait un tour sur elle-même, c-à-d tourne de 360°, en 24 heures de temps sidéral (mais pas 24 h de temps civil, comme expliqué plus haut). Il est donc parfaitement logique de considérer que le temps sidéral est un angle, et qu'une heure de temps sidéral correspond à 15°.
Sachant qu'un objet astronomique se trouve plein sud lorsque le temps sidéral est égal à son ascension droite, il est raisonnable de donner un nom à leur différence. Les astronomes la nomment l'angle horaire (hour angle), que nous noterons H ici :
\[ H = S_l - \alpha \]
Cette définition implique que l'angle horaire d'un objet vaut 0 quand il est plein sud.
2.5 Calcul du temps sidéral
Pour calculer le temps sidéral (local), on commence par calculer le temps sidéral de Greenwich — c-à-d celui à la longitude 0° — au moyen d'une formule approximative, puis on l'ajuste en fonction de la longitude du lieu.
Pour déterminer le temps sidéral de Greenwich pour un instant — c-à-d un couple date/heure — donné, il faut tout d'abord exprimer cet instant dans le fuseau horaire de Greenwich (UTC), avant de déterminer :
- le nombre de siècles juliens séparant l'époque J2000 et le début du jour contenant l'instant (c-à-d 0h ce jour-là), sachant qu'un siècle julien correspond à 36525 jours,
- le nombre d'heures séparant le début du jour contenant l'instant et l'instant lui-même.
En notant la première de ces valeurs T et la seconde t, on peut ensuite calculer les deux termes suivants :
\begin{align*} S_0 &= 0.000025862\,T^2 + 2400.051336\,T + 6.697374558\\ S_1 &= 1.002737909\,t \end{align*}qu'on additionne finalement pour obtenir le temps sidéral de Greenwich, \(S_g\) :
\[S_g = S_0 + S_1 \]
Attention toutefois : le résultat obtenu au moyen de cette formule est en heures, pas en radians, et il n'est pas normalisé à l'intervalle [0, 24h[.
Une fois le temps sidéral de Greenwich déterminé, le temps sidéral local propre à un endroit donné, \(S_l\) se détermine par la simple addition de la longitude λ du lieu :
\[ S_l = S_g + \lambda \]
Référence : Practical Astronomy with your Calculator or Spreadsheet, §12
2.6 Conversion écliptique vers équatoriale
Les coordonnées écliptiques et équatoriales ont été décrite à l'étape précédente.
Pour mémoire, les coordonnées écliptiques sont la longitude écliptique, notée λ, et la latitude écliptique, notée β, tandis que les coordonnées équatoriales sont l'ascension droite, notée α, et la déclinaison, notée δ. La conversion des premières vers les secondes se fait au moyen des formules suivantes :
\begin{align*} \alpha &= \arctan\left[\frac{\sin\lambda\,\cos\varepsilon - \tan\beta\,\sin\varepsilon}{\cos\lambda}\right]\\[0.5em] \delta &= \arcsin\left[\sin\beta\,\cos\varepsilon + \cos\beta\,\sin\varepsilon\,\sin\lambda\right] \end{align*}où \(\varepsilon\) est l'obliquité de l'écliptique, c-à-d l'angle entre le plan de l'équateur et celui de l'écliptique — ou, ce qui revient au même, l'angle d'inclinaison de l'axe de rotation de la Terre par rapport à l'écliptique.
Cet angle vaut environ 23.5°, mais il varie au cours du temps, et nous utiliserons donc la fonction polynomiale suivante pour déterminer sa valeur approximative avec une précision suffisante pour nos besoins :
\[ \varepsilon =\,0.00181^{\prime\prime}\,T^3 - 0.0006^{\prime\prime}\,T^2 - 46.815^{\prime\prime}\,T + 23°26^\prime21.45^{\prime\prime} \]
où \(T\) est le nombre de siècles juliens (36525 jours) écoulés depuis l'époque J2000.
Référence : Practical Astronomy with your Calculator or Spreadsheet, §27
2.7 Conversion équatoriale vers horizontale
Les coordonnées horizontales ont également été décrites à l'étape précédente. Pour mémoire, il s'agit de l'azimut, noté A, et la hauteur, notée h. Les formules suivantes permettent d'obtenir ces coordonnées à partir des coordonnées équatoriales :
\begin{align*} A &= \arctan\left[\frac{-\cos\delta\,\cos\phi\,\sin H}{\sin\delta - \sin\phi\,\sin h}\right]\\[0.5em] h &= \arcsin\left[\sin\delta\,\sin\phi + \cos\delta\,\cos\phi\,\cos H\right] \end{align*}Dans ces formules, ϕ est la latitude de l'observateur, tandis que H est l'angle horaire.
Référence : Practical Astronomy with your Calculator or Spreadsheet, §25
3 Mise en œuvre Java
Les classes et types énumérés à écrire pour cette étape appartiennent à deux sous-paquetages du paquetage ch.epfl.rigel.
Le premier, coordinates, a déjà été introduit à l'étape précédente. Le second, astronomy, contiendra un certain nombre de classes spécifiques à l'astronomie. Comme précédemment, le nom de ces paquetages est souvent abrégé ci-dessous en remplaçant tous ses composants sauf le dernier par une ellipse (…).
Avant de décrire les classes à écrire dans le cadre de cette étape, il importe toutefois de dire quelques mots au sujet du paquetage java.time de la bibliothèque Java, qui contient de nombreuses classes permettant de travailler avec le temps (civil).
3.1 Le paquetage java.time
Astronomie et temps sont intimement liés, d'une part car le temps joue un rôle essentiel en astronomie, et d'autre part car les notions temporelles que nous utilisons tous les jours sont basées sur des phénomènes astronomiques, comme nous l'avons vu plus haut avec l'exemple de la durée du jour.
Les calculs liés au temps sont généralement assez complexes. Par exemple, déterminer le temps exact séparant deux couples date/heure implique de tenir compte des fuseaux horaires utilisés, de l'éventuelle heure d'été en vigueur, des années bissextiles, etc. Il n'est dès lors pas surprenant que les concepteurs de la bibliothèque Java aient dû s'y reprendre à trois fois avant de réussir à offrir un ensemble de classes de gestion du temps qui soit de bonne qualité.
La dernière — et de loin la meilleure — version de ces classes se trouve dans le paquetage java.time, que nous allons utiliser intensivement dans ce projet. Les classes qu'il contient sont fort bien conçues, mais assez difficile à appréhender en raison de la complexité du sujet qu'elles traitent.
Nous vous suggérons donc de vous familiariser rapidement avec les classes ci-dessous, en lisant le texte de description se trouvant au sommet de leur documentation, et en regardant brièvement les méthodes qu'elles offrent :
LocalDate, qui représente une date sans information de temps ou de fuseau horaire, p.ex. « le 24 février 2020 »,LocalTime, qui représente un instant de la journée, sans information de date ni de fuseau horaire, p.ex. « 13h25 »LocalDateTime, qui représente un couple date/heure sans information de fuseau horaire, p.ex. « 24 février 2020 à 13h25 »,ZonedDateTime, qui représente un couple date/heure avec fuseau horaire, p.ex. « 24 février 2020 à 13h25 dans le fuseau horaire de Zürich ».
N'hésitez pas à écrire de petits programmes utilisant ces classes afin de mieux les comprendre.
3.2 Énumération Epoch
L'énumération (ou type énuméré) Epoch du paquetage ….astronomy représente une époque astronomique. Ses membres, nommés J2000 et J2010, représentent les deux époques décrites à la §2.1.
L'énumération Epoch offre deux méthodes publiques :
double daysUntil(ZonedDateTime when), qui retourne le nombre de jours (pas forcément entier !) entre l'époque à laquelle on l'applique (this) et l'instantwhen, les valeurs négatives correspondant à des dates antérieures à l'époque, les valeurs positives à des dates postérieures,double julianCenturiesUntil(ZonedDateTime when), qui retourne le nombre de siècles juliens entre l'époque à laquelle on l'applique etwhen, de manière similaire àdaysUntil.
Notez bien que ces deux méthodes ne retournent pas forcément des valeurs entières. Par exemple, l'extrait de programme suivant :
ZonedDateTime d = ZonedDateTime.of( LocalDate.of(2000, Month.JANUARY, 3), LocalTime.of(18, 0), ZoneOffset.UTC); System.out.println(J2000.daysUntil(d));
doit afficher 2.25, car l'écart entre J2000 et le 3 janvier 2000 à 18h00 est de 2 jours et 6h, soit 2.25 jours.
3.2.1 Notes de programmation
- Membres de types énumérés
Pour mémoire, les types énumérés Java peuvent posséder des attributs, des méthodes et des constructeurs (privés uniquement).
L'exemple ci-dessous, dont vous pouvez vous inspirer, rappelle la syntaxe :
public enum Season { SPRING("printemps"), SUMMER("été"), AUTUMN("automne"), WINTER("hiver"); private String frenchName; private Season(String frenchName) { this.frenchName = frenchName; } public String frenchName() { return frenchName; } }Pour plus de détails, reportez-vous au cours du semestre précédent, en particulier à la leçon de la semaine 10 sur les types énumérés.
- Définition de
J2010
Pour définir
J2010, vous ne pouvez pas directement utiliser la date du 0 janvier, car une expression comme celle-ci lève une exception :LocalDate.of(2010, Month.JANUARY, 0)
Pour résoudre ce problème, vous pouvez soit utiliser la date du 31 décembre 2009, soit soustraire un jour du 1 janvier 2010. Cette seconde solution nous paraît légèrement préférable, car le lien entre le nom de l'époque et sa valeur est alors plus évident. L'expression suivante permet de faire cette soustraction :
LocalDate.of(2010, Month.JANUARY, 1).minusDays(1)
- Temps écoulé entre deux dates
Pour déterminer le temps écoulé entre deux dates, comme
daysUntiletjulianCenturiesUntildoivent le faire, il faut bien entendu utiliser des méthodes offertes par le paquetagejava.time.En particulier, il faut noter que la classe
ZonedDateTimeoffre la méthodeuntilqui semble correspondre exactement à nos besoins. Elle souffre toutefois d'un petit défaut, qui est qu'elle retourne toujours une valeur arrondie par défaut, ce qui ne devrait pas être le cas des méthodes deEpoch, comme illustré plus haut.Ce problème peut toutefois être résolu assez facilement, en utilisant la méthode
untilpour déterminer le nombre de millisecondes séparant les deux dates, puis en convertissant la valeur obtenue à l'unité appropriée. Pour obtenir cette valeur, passez la constanteMILLISde l'énumérationChronoUniten second argument à la méthodeuntil.
3.3 Classe SiderealTime
La classe SiderealTime du paquetage ….astronomy, publique, finale et non instanciable, contient deux méthodes statiques permettant de calculer le temps sidéral, qui sont :
double greenwich(ZonedDateTime when), qui retourne le temps sidéral de Greenwich, en radians et compris dans l'intervalle [0, τ[, pour le couple date/heurewhen,double local(ZonedDateTime when, GeographicCoordinates where), qui retourne le temps sidéral local, en radians et compris dans l'intervalle [0, τ[, pour le couple date/heurewhenet la positionwhere.
Notez bien que ces méthodes doivent retourner une valeur en radians, alors que les formules données plus haut — provenant de notre livre de référence — travaillent en heures.
3.3.1 Conseils de programmation
Les méthodes withZoneSameInstant et truncatedTo de ZonedDateTime peuvent être utiles pour écrire les méthodes de SiderealTime.
3.4 Classe EclipticToEquatorialConversion
La classe EclipticToEquatorialConversion du paquetage ….coordinates, publique, finale et immuable, représente un changement de système de coordonnées depuis les coordonnées écliptiques vers les coordonnées équatoriales, à un instant donné. Elle implémente l'interface suivante :
Function<EclipticCoordinates, EquatorialCoordinates>
Function est définie dans le paquetage java.util.function de la bibliothèque standard Java. L'intérêt d'implémenter cette interface est expliqué à la §3.6.
La classe EclipticToEquatorialConversion offre un unique constructeur public :
EclipticToEquatorialConversion(ZonedDateTime when), qui construit un changement de système de coordonnées entre les coordonnées écliptiques et les coordonnées équatoriales pour le couple date/heurewhen.
EclipticToEquatorialConversion offre une définition de l'unique méthode abstraite de l'interface Function :
EquatorialCoordinates apply(EclipticCoordinates ecl), qui retourne les coordonnées équatoriales correspondant aux coordonnées écliptiquesecl.
Finalement, la classe EclipticToEquatorialConversion redéfinit les méthodes hashCode et equals pour qu'elles lèvent UnsupportedOperationException.
3.4.1 Conseils de programmation
- Tangente inverse
Pour calculer la tangente inverse, il vous faut utiliser la méthode
atan2de la classeMath, et non pas la méthodeatan, cette dernière n'ayant pas assez d'information pour retourner le bon résultat. - Performances
Une fois terminé, votre programme devra faire un très grand nombre de changements de système de coordonnées pour dessiner le ciel. Il est donc capital que ceux-ci puissent se faire aussi rapidement que possible.
Cela implique que votre classe
EclipticToEquatorialConversiondoit impérativement calculer toutes les valeurs qui ne dépendent pas des coordonnées à transformer au moment de sa construction, et les stocker dans des attributs privés.Par exemple, le cosinus de l'obliquité de l'écliptique ne dépend que de l'instant à laquelle la transformation est faite, et peut donc être stocké dans un attribut privé. Il en va de même d'au moins une autre valeur, que nous vous laissons le soin de découvrir.
Attention : n'ignorez pas la remarque qui précède, faute de quoi vous pourriez être sanctionnés à ce sujet au moment du rendu intermédiaire.
3.5 Classe EquatorialToHorizontalConversion
La classe EquatorialToHorizontalConversion du paquetage ….coordinates, publique, finale et immuable, représente un changement de système de coordonnées depuis les coordonnées équatoriales vers les coordonnées écliptiques, à un instant et pour un lieu donnés. Elle offre un unique constructeur public :
EquatorialToHorizontalConversion(ZonedDateTime when, GeographicCoordinates where), qui construit un changement de système de coordonnées entre les coordonnées équatoriales et les coordonnées horizontales pour le couple date/heurewhenet le lieuwhere.
De manière similaire à la classe précédente, celle-ci implémente l'interface suivante :
Function<EquatorialCoordinates, HorizontalCoordinates>
et offre donc une mise en œuvre de la méthode abstraite provenant de cette interface :
HorizontalCoordinates apply(EquatorialCoordinates equ), qui retourne les coordonnées horizontales correspondant aux coordonnées équatorialesequ.
Finalement, elle redéfinit hashCode et equals de la même manière que la classe précédente.
Notez que les remarques de la §3.4.1 au sujet de la tangente inverse et des performances s'appliquent également à cette classe.
3.6 Composition de conversions
Au moyen des deux classes de conversion définies ci-dessus, il est facile d'effectuer une conversion depuis les coordonnées écliptiques vers les coordonnées horizontales. Il suffit pour cela d'enchaîner les deux conversions, en appliquant d'abord la première conversion aux coordonnées écliptiques, pour obtenir des coordonnées équatoriales, puis de leur appliquer la seconde conversion, afin d'obtenir des coordonnées horizontales.
L'extrait de programme suivant illustre cet enchaînement d'appels, qui apparaît à la dernière ligne :
EclipticCoordinates ecl = …; // coordonnées à convertir EclipticToEquatorialConversion eclToEqu = …; // conv. 1 EquatorialToHorizontalConversion equToHor = …; // conv. 2 HorizontalCoordinates hor = equToHor.apply(eclToEqu.apply(ecl));
Toutefois, étant donné que les deux classes de conversion implémentent l'interface Function, il est possible de créer un objet représentant la combinaison des deux conversions ! Cela peut se faire au moyen de la méthode andThen, définie (par défaut) dans l'interface Function et donc héritée par les classes de conversion. L'exemple ci-dessous illustre cela :
// Composition des conversions 1 et 2! Function<EclipticCoordinates,HorizontalCoordinates> eclToHor = eclToEqu.andThen(equToHor); HorizontalCoordinates hor = eclToHor.apply(ecl);
Comme son nom l'indique, andThen enchaîne deux fonctions en appliquant d'abord la première (le récepteur), puis la seconde. Le type de l'objet eclToHor se lit « une fonction prenant un argument de type EclipticCoordinates et retournant une valeur de type HorizontalCoordinates ».
3.7 Tests
Comme pour l'étape précédente, nous ne vous fournissons plus de tests mais un fichier de vérification de signatures contenu dans une archive Zip à importer dans votre projet.
Pour écrire vos tests, nous vous conseillons fortement de vous reporter au livre de référence, Practical Astronomy with your Calculator or Spreadsheet, en particulier à :
- la §12, p. 23, qui contient un exemple de calcul du temps sidéral de Greenwich,
- la §27, p. 51, qui contient un exemple de calcul de l'obliquité de l'écliptique.
4 Résumé
Pour cette étape, vous devez :
- écrire le type énuméré
Epochet les classesSiderealTime,EclipticToEquatorialConversionetEquatorialToHorizontalConversionselon les instructions ci-dessus, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 6 mars 2020 à 17h00, via le système de rendu.
Ce rendu est un rendu testé, auquel 18 points sont attribués, au prorata des tests unitaires passés avec succès.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus. Souvenez-vous qu'aucun retard, aussi insignifiant soit-il, ne sera toléré !