Classes mathématiques
Rigel – étape 1
1 Introduction
Le but principal de cette première étape est d'écrire plusieurs classes permettant de manipuler trois concepts mathématiques utiles dans le cadre du projet : les intervalles, les fonctions polynomiales et les angles.
Comme toutes les descriptions d'étapes de ce projet, celle-ci commence par une introduction aux concepts nécessaires à sa réalisation (§2), avant de présenter leur mise en œuvre en Java (§3).
Avant de continuer, vous êtes toutefois priés de lire les guides Travailler en groupe et Synchroniser son travail qui vous donneront des informations vous permettant de bien vous organiser.
2 Concepts
2.1 Intervalles
En mathématiques, un intervalle (réel) ([real] interval en anglais) est l'ensemble de tous les nombres réels compris entre deux d'entre eux, qui constituent respectivement la borne inférieure (a ci-dessous) et la borne supérieure (b ci-dessous) de l'intervalle.
Un intervalle peut être ouvert ou fermé de chaque côté (à gauche et à droite), ce qui détermine si la borne correspondante est incluse ou non dans l'ensemble : si l'ensemble est fermé d'un côté, la borne correspondante en fait partie, sinon elle n'en fait pas partie.
Il existe donc quatre sortes d'intervalles que l'on note, définit et nomme de la manière suivante :
- \(]a,b[\,= \{ x\in\Bbb{R}\ |\ a \lt x \lt b\}\) : intervalle ouvert,
- \(]a,b]\,= \{ x\in\Bbb{R}\ |\ a \lt x \le b\}\) : intervalle semi-ouvert à gauche,
- \([a,b[\,= \{ x\in\Bbb{R}\ |\ a \le x \lt b\}\) : intervalle semi-ouvert à droite,
- \([a,b]\,= \{ x\in\Bbb{R}\ |\ a \le x \le b\}\) : intervalle fermé.
Un intervalle est de plus dit non trivial s'il contient plus d'un élément, c-à-d si a < b. La taille d'un tel intervalle est simplement la différence entre sa borne supérieure et sa borne inférieure, à savoir b – a.
Dans le cadre de ce projet, nous n'utiliserons que deux types d'intervalles, les semi-ouverts à droite et les fermés, toujours non triviaux. Nous définirons de plus deux fonctions sur ces intervalles :
- l'écrêtage, défini sur les intervalles fermés,
- la réduction, définie sur les intervalles semi-ouverts à droite.
Le but de ces deux fonctions est de ramener une valeur quelconque à la valeur de l'intervalle qui lui correspond, mais elles le font de manière différente, comme expliqué ci-après.
2.1.1 Écrêtage
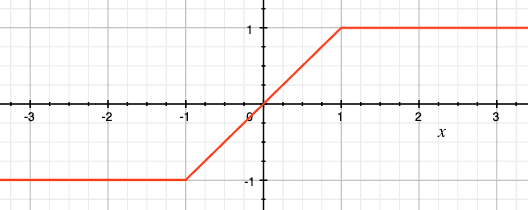
Soit un intervalle fermé \([a,b]\). La fonction d'écrêtage correspondant à cet intervalle, nommée clip, est définie ainsi :
\[ \text{clip}_{[a,b]}(x) = \begin{cases} a & \text{si \(x \le a\)}\\ b & \text{si \(x \ge b\)}\\ x & \text{sinon} \end{cases} \]
La figure 1 ci-dessous montre le graphe de cette fonction pour l'intervalle \([-1,1]\).
2.1.2 Réduction
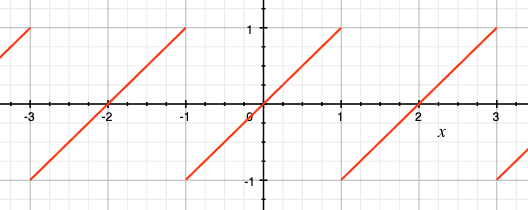
Soit un intervalle semi-ouvert à droite \([a,b[\). La fonction de réduction correspondant à cet intervalle, nommée reduce, est définie ainsi :
\[ \text{reduce}_{[a,b[}(x) = a + \text{floorMod}(x - a, b - a) \]
où floorMod est le reste de la partie entière par défaut, défini ainsi :
\[ \text{floorMod}(x, y) = x - y\left\lfloor\frac{x}{y}\right\rfloor \]
où \(\left\lfloor\cdot\right\rfloor\) dénote la partie entière par défaut (floor en anglais).
Dans ce projet, la réduction sera principalement utile pour ramener des angles quelconques à un intervalle standard. Par exemple, en réduisant l'angle 200° à l'intervalle [–180°,180°[, on obtient l'angle équivalent de –160°.
La figure 2 ci-dessous montre le graphe de cette fonction pour l'intervalle \([-1,1[\).
2.2 Fonctions polynomiales
Une fonction polynomiale de degré n est une fonction f ayant la forme suivante :
\[ f(x) = c_n\,x^n + c_{n-1}\,x^{n-1} + \cdots + c_1\,x + c_0 \]
où les \(c_j\) sont des nombres réels, appelés les coefficients de la fonction. Cette fonction peut s'écrire de manière équivalente sous la forme dite de Horner :
\[ f(x) = ((\cdots(c_n\,x + c_{n-1})\,x + \cdots) + c_1)\,x + c_0 \]
La forme de Horner présente l'avantage de ne nécessiter aucune élévation à la puissance, et d'être donc plus efficace à calculer.
2.3 Angles
Les angles peuvent être représentés au moyen de différentes unités, par exemple les radians ou les degrés, ayant chacune leurs avantages et inconvénients.
Ainsi, pour les calculs, l'unité la plus naturelle est le radian. C'est d'ailleurs la seule unité utilisée par les méthodes trigonométriques (sinus, cosinus, etc.) de Java et de la plupart des langages de programmation. Par contre, pour les êtres humains, les radians sont peu agréables à utiliser. Pour cette raison, deux autres unités leur sont souvent préférées en astronomie : les degrés et les heures.
Les sections qui suivent décrivent les trois unités d'angle susmentionnées.
2.3.1 Radians
En radians, un tour fait 2π rad.
Afin de simplifier quelque peu les formules, il a été suggéré à plusieurs reprises de définir une nouvelle constante valant 2π, par exemple τ (la lettre grecque tau). Nous adopterons cette convention dans ce projet en posant :
\[ \tau = 2\pi \]
Dès lors, en radians, un tour fait τ rad.
2.3.2 Degrés
En degrés, un tour fait 360°. On a donc l'équivalence suivante entre les degrés et les radians :
\[ 360° = τ\ \mathrm{rad} \]
Lorsqu'un angle n'est pas représentable au moyen d'un nombre entier de degrés, deux conventions existent pour représenter la partie fractionnaire :
- la notation décimale classique,
- la notation sexagésimale.
La notation décimale consiste à représenter les fractions d'angles au moyen de chiffres placés après le séparateur décimal, qui est soit le point (.), soit la virgule (,). Ainsi, l'angle « dix degrés et demi » est représenté par le nombre 10,5° ou 10.5°.
La notation sexagésimale consiste à représenter les fractions d'angles au moyen de deux autres composantes, les minutes et les secondes d'arc. Ainsi, un degré est découpé en 60 minutes d'arc (arc minutes en anglais), et chacune d'entre elles est découpée en 60 secondes d'arc (arc seconds). Les secondes d'arc ne sont pas découpées en sous-unités, et on utilise dès lors la notation décimale classique lorsqu'on désire représenter les fractions de secondes.
Lorsqu'un angle est représenté en notation sexagésimale, la composante des degrés est suivie comme d'habitude du signe des degrés (°), tandis que les minutes d'arc sont suivies du symbole prime (′) et les secondes d'arc du symbole double prime (″). Par exemple, l'angle « dix degré et demi » est représenté en notation sexagésimale comme 10° 30′.
La notation sexagésimale des angles est similaire à la notation habituelle des heures de la journée, également découpées en 60 minutes de 60 secondes chacune. Il faut toutefois prendre garde au fait qu'en astronomie, le terme heure désigne également une mesure d'angle (!), décrite à la section suivante.
2.3.3 Heures
En heures, un tour fait 24 h. On a donc les équivalences suivantes :
\begin{align*} 24\ \mathrm{h} &= 360° = \tau\ \mathrm{rad}\\ 1\ \mathrm{h} &= 15° \end{align*}Là aussi, les fractions d'heures sont représentées soit en notation décimale classique, soit en notation sexagésimale. La seule différence est que les symboles h, m et s sont utilisés en lieu et place de °, ′ et ″. Par exemple, l'angle « dix degrés et demi » peut s'écrire soit comme 0.7 h, soit comme 0h 42m.
Il faut noter que lorsqu'un angle est exprimé en heure et que la notation sexagésimale est utilisée, rien ne le distingue syntaxiquement d'une heure du jour ou d'une durée. Ainsi, la séquence de caractères « 11h 30m 20s » peut désigner aussi bien une heure du jour (un peu moins d'une demi-heure avant midi), une durée ou un angle. Le contexte permet généralement de savoir laquelle de ces interprétations est la bonne.
2.3.4 Représentation normale
Indépendamment de l'unité et de la notation utilisées, il existe toujours plusieurs manières équivalentes de représenter un angle donné. Par exemple, l'angle 120° peut aussi s'écrire –240° ou encore 360120°. De manière générale, on peut toujours ajouter ou soustraire un nombre quelconque (mais entier) de tours à un angle pour obtenir un angle équivalent.
Le fait qu'un angle ait plusieurs représentations est généralement peu agréable, et il est donc fréquent que des conventions dictent quelle représentation utiliser pour un angle, parmi toutes celles possibles. Nous appellerons cette représentation la représentation normale.
Comme nous le verrons par la suite, la convention utilisée dépend de la situation. Par exemple, un angle représentant une longitude géographique est toujours représenté au moyen de l'unique angle équivalent appartenant à l'intervalle [–180°,180°[. Pour les azimuts, par contre, c'est l'angle appartenant à l'intervalle [0°,360°[ qui est utilisé. Etc.
3 Mise en œuvre Java
Les concepts importants pour cette étape ayant été introduits, il est temps de décrire leur mise en œuvre en Java.
En plus des classes permettant de représenter les concepts mathématiques expliqués ci-dessus, une classe « utilitaire » est à réaliser : Preconditions, qui offre des méthodes de validation d'arguments.
Notez que toutes les classes et interfaces de ce projet appartiendront au paquetage ch.epfl.rigel ou à l'un de ses sous-paquetages.
Attention : jusqu'à l'étape 6 du projet (incluse), vous devez suivre à la lettre les instructions qui vous sont données dans l'énoncé, et vous n'avez pas le droit d'apporter la moindre modification à l'interface publique des classes, interfaces et types énumérés décrits. Vous pouvez par contre définir des méthodes et attributs privés si cela vous semble judicieux.
3.1 Installation de Java
Avant de commencer à programmer, il faut vous assurer que la version 11 de Java est bien installée sur votre ordinateur, car c'est celle qui sera utilisée pour ce projet.
Si vous n'avez pas encore installé cette version, rendez-vous sur le site Web du projet AdoptOpenJDK, téléchargez le programme d'installation correspondant à votre système d'exploitation (macOS, Linux ou Windows), et exécutez-le. Ensuite, si vous utilisez Eclipse plutôt qu'IntelliJ, lisez le guide Configurer Eclipse et suivez les indications qui s'y trouvent.
3.2 Classe Preconditions
Fréquemment, les méthodes d'un programme s'attendent à ce que leurs arguments satisfassent certaines conditions. Par exemple, une méthode déterminant la valeur maximale d'un tableau d'entiers s'attend à ce que ce tableau ne soit pas vide.
De telles conditions sont souvent appelées préconditions car elles doivent être satisfaites avant l'appel d'une méthode : c'est à l'appelant de s'assurer qu'il n'appelle la méthode qu'avec des arguments valides.
En Java, la convention veut que chaque méthode vérifie ses préconditions et lève une exception — souvent IllegalArgumentException — si l'une d'entre elles n'est pas satisfaite. Par exemple, une méthode max calculant la valeur maximale d'un tableau d'entiers pourrait commencer ainsi :
int max(int[] array) {
if (! (array.length > 0))
throw new IllegalArgumentException();
// … reste du code
}
(Notez au passage que la méthode max ne déclare pas qu'elle lève potentiellement IllegalArgumentException au moyen d'une clause throws, car cette exception est de type unchecked.)
La première classe à réaliser dans le cadre de ce projet a pour but de faciliter l'écriture de telles préconditions. En l'utilisant, la méthode ci-dessus pourrait être simplifiée ainsi :
import static ch.epfl.rigel.Preconditions.checkArgument;
int max(int[] array) {
checkArgument(array.length > 0);
// … reste du code
}
Cette classe est nommée Preconditions et appartient au paquetage ch.epfl.rigel. Elle est publique et finale et n'offre rien d'autre que deux méthodes statiques décrites plus bas. Elle a toutefois la particularité d'avoir un constructeur par défaut privé :
public final class Preconditions {
private Preconditions() {}
// … méthodes
}
Le but de ce constructeur privé est de rendre impossible la création d'instances de la classe, puisque cela n'a clairement aucun sens — elle ne sert que de conteneur à un ensemble de méthodes statiques. Dans la suite du projet, nous définirons plusieurs autres classes du même type, que nous appellerons dès maintenant classes non instanciables.
Les deux méthodes publiques (et statiques) de la classe Preconditions sont :
void checkArgument(boolean isTrue), qui lève l'exceptionIllegalArgumentExceptionsi son argument est faux, et ne fait rien sinon,double checkInInterval(Interval interval, double value), qui lève l'exceptionIllegalArgumentExceptionsivaluen'appartient pas àinterval, et retournevaluesinon.
Notez que pour écrire la seconde méthode, il vous faut d'abord écrire la classe Interval décrite à la §3.3.
3.3 Classe Interval
La classe Interval du paquetage ch.epfl.rigel.math, publique, abstraite et immuable, représente un intervalle. Elle a pour but de servir de classe mère aux deux classes représentant respectivement un intervalle fermé et un intervalle semi-ouvert à droite, décrites plus bas (§3.4 et §3.5).
La classe Interval possède un unique constructeur, protégé, qui prend en argument les bornes de l'intervalle et les stocke dans des attributs privés et finaux.
En plus de ce constructeur, elle offre les méthodes publiques suivantes :
double low(), qui retourne la borne inférieure de l'intervalle,double high(), qui retourne la borne supérieure de l'intervalle,double size(), qui retourne la taille de l'intervalle.
De plus, la classe Interval définit une méthode abstraite que les sous-classes doivent redéfinir :
boolean contains(double v), qui retourne vrai ssi — si et seulement si — la valeurvappartient à l'intervalle.
Finalement, la classe Interval redéfinit les méthodes hashCode et equals de Object afin qu'elles lèvent l'exception UnsupportedOperationException. Pour garantir qu'aucune sous-classe ne les redéfinira, ces méthodes sont déclarées finales.
Il peut paraître étrange de demander que la méthode equals (et hashCode, qui est liée à equals et sera examinée plus tard dans le cours) lève une exception. Après tout, n'est-il pas raisonnable de tester si deux intervalles sont égaux ?
Mathématiquement, la réponse est clairement oui : deux intervalles sont égaux si — et seulement si — ils sont du même type et leurs bornes sont égales.
En Java, les choses sont plus délicates car les bornes ne sont pas vraiment des nombres réels, mais une approximation sous forme de nombres à virgule flottante — de type float ou double. Or cette approximation a une précision limitée, qui implique que certaines valeurs mathématiquement égales ne le sont pas lorsqu'on les représente au moyen de nombres à virgule flottante.
Par exemple, mathématiquement, l'égalité suivante est vraie :
\[ 0.1 + 0.2 = 0.15 + 0.15 \]
Or en Java (et dans la plupart des langages de programmation actuels), cette même égalité est fausse ! Ainsi, l'extrait de programme suivant affiche false et pas true comme on pourrait le penser :
System.out.println(0.1 + 0.2 == 0.15 + 0.15);
Pour cette raison, dans ce projet nous avons choisi de ne jamais tester l'égalité de nombres à virgule flottante.
Une conséquence de ce choix est que la méthode equals de Interval ne peut rien faire d'autre que lever une exception, car elle n'a pas le droit de tester l'égalité des bornes des intervalles à comparer, comme elle devrait théoriquement le faire. Cela sera vrai pour de nombreuses autres classes de ce projet, à commencer par toutes celles dont au moins un attribut est un nombre à virgule flottante.
On peut se demander s'il n'aurait pas été préférable de simplement hériter les méthodes equals et hashCode de Object, sans les redéfinir. Malheureusement, cette solution n'est pas bonne non plus, car la notion d'égalité aurait alors été basée sur l'identité des objets, ce qui n'a pas vraiment de sens pour une classe immuable, comme nous le verrons ultérieurement dans le cours.
3.4 Classe ClosedInterval
La classe ClosedInterval du paquetage ch.epfl.rigel.math, publique, finale et immuable, représente un intervalle fermé. Elle hérite bien entendu de la classe Interval.
Son constructeur est privé, mais elle offre des méthodes publiques et statiques de construction permettant de créer un intervalle fermé de deux manières différentes :
ClosedInterval of(double low, double high), qui retourne un intervalle fermé allant delowàhigh, ou lèveIllegalArgumentExceptionsi la borne inférieurelown'est pas (strictement) plus petite que la borne supérieurehigh,ClosedInterval symmetric(double size), qui retourne un intervalle fermé centré en 0 et de taillesize, ou lèveIllegalArgumentExceptionsi la taille n'est pas (strictement) positive.
En plus de la définition de la méthode contains, la classe ClosedInterval définit la méthode suivante :
double clip(double v), qui écrête son argument à l'intervalle (voir §2.1.1).
Finalement, la classe ClosedInterval redéfinit la méthode toString de Object afin qu'elle retourne la représentation textuelle de l'intervalle, formée de la borne inférieure et de la borne supérieure, séparées par une virgule et entourées de crochets droits. (Voir à ce sujet les conseils de programmation qui suivent.)
3.4.1 Conseils de programmation
Pour construire la chaîne retournée par toString, il est bien entendu possible d'utiliser l'opérateur + de concaténation de chaînes. Cela dit, une autre option existe, et nous vous conseillons de l'utiliser car elle sera souvent utile dans le projet.
Cette option consiste à utiliser la méthode format de la classe String, qui accepte un nombre variable d'arguments qui sont :
- un objet décrivant les conventions de formatage spécifiques à l'utilisateur, comme p.ex. le séparateur décimal à utiliser (point ou virgule),
- une chaîne de formatage (format string), qui est une chaîne de caractères contenant généralement une ou plusieurs spécifications de format (format specifiers) qui commencent par le signe pourcent (
%), - zéro ou plusieurs valeurs dont la représentation textuelle est à insérer dans la chaîne de formatage en lieu et place des spécifications de format correspondantes, comme décrit plus bas.
Dans le cadre de ce projet, il vous est demandé de toujours passer la constante Locale.ROOT comme premier argument. Cela garantit que le point est toujours utilisé comme séparateur décimal, même si votre ordinateur est configuré pour utiliser la virgule.
Le second argument est une chaîne de formatage, dont la syntaxe est décrite en détail dans la documentation de la classe Formatter du paquetage java.util. Cette documentation est toutefois assez longue et indigeste, raison pour laquelle nous vous proposons les exemples ci-dessous qui devraient vous suffire pour ce projet.
Pour illustrer l'utilisation de la méthode format, imaginons une méthode nommée constantDescription prenant en argument un nom de constante et sa valeur (de type double), et qui retourne une chaîne décrivant la constante. Une manière d'écrire cette méthode est d'utiliser l'opérateur de concaténation de chaîne, ainsi :
String constantDescription(String name, double value) {
return "La constante " + name + " vaut " + value + ".";
}
On pourrait utiliser cette méthode pour afficher la valeur de la constante PI de la classe Math :
// Affiche "La constante π vaut 3.141592653589793."
System.out.println(constantDescription("π", Math.PI));
Au moyen de la méthode format de String, la méthode constantDescription peut s'écrire de manière tout à fait équivalente ainsi :
String constantDescription(String name, double value) {
return String.format(Locale.ROOT,
"La constante %s vaut %s.",
name,
value);
}
Comme cet exemple l'illustre, format retourne une chaîne identique à la chaîne de formatage, si ce n'est que les deux spécifications de format %s sont remplacées par la représentation textuelle des arguments donnés, à savoir name et value. C'est en effet la signification de la spécification de format %s, la lettre s voulant dire string.
Jusqu'ici l'intérêt de la méthode format semble limité, la seconde version de la méthode constantDescription étant plus longue — et pas forcément plus claire — que la première. Toutefois, imaginons maintenant que l'on désire afficher la valeur de la constante avec exactement 2 décimales. Comment adapter nos deux versions de constantDescription dans ce but ?
La première version, celle qui utilise la concaténation de chaîne, est malheureusement très pénible à adapter, et nous laissons donc cette adaptation en exercice.
La seconde version est par contre très facile à adapter, puisqu'il suffit de remplacer la seconde spécification de format (c-à-d la seconde occurrence de %s) par la spécification %.2f. Cette nouvelle spécification signifie que l'argument qui lui correspond est un nombre à virgule flottante (floating point, d'où l'utilisation de la lettre f) et qu'il doit être représenté avec exactement deux décimales, comme indiqué par le .2. On obtient alors la définition suivante :
String constantDescription(String name, double value) {
return String.format(Locale.ROOT,
"La constante %s vaut %.2f.",
name,
value);
}
En l'utilisant sur notre exemple précédent, on obtient bien le résultat escompté :
// Affiche "La constante π vaut 3.14."
System.out.println(constantDescription("π", Math.PI));
3.5 Classe RightOpenInterval
La classe RightOpenInterval du paquetage ch.epfl.rigel.math, publique, finale et immuable, représente un intervalle semi-ouvert à droite. Elle hérite bien entendu de la classe Interval.
Tout comme ClosedInterval, son constructeur est privé mais elle offre les deux mêmes méthodes de construction statiques que ClosedInterval, à savoir of et symmetric, mais qui retournent bien entendu un intervalle semi-ouvert à droite.
En plus de la définition de la méthode contains, la classe RightOpenInterval définit la méthode publique suivante :
double reduce(double v), qui réduit son argument à l'intervalle (voir §2.1.2).
Finalement, la classe RightOpenInterval redéfinit la méthode toString de Object de manière similaire à la classe ClosedInterval, la différence étant bien entendu que le crochet terminant cette chaîne est ouvrant ([) et pas fermant (]).
3.6 Classe Angle
Dans ce projet, nous avons choisi de représenter les angles au moyen de simples nombres à virgule flottante de type double, dont la valeur est celle de l'angle, généralement exprimée en radians.
Il aurait bien entendu aussi été possible de définir une classe représentant un angle. Cette solution, peut-être plus conforme à la « philosophie orientée-objet », aurait toutefois été un peu lourde à l'usage, raison pour laquelle nous ne l'avons pas retenue.
L'inconvénient principal de la solution choisie est qu'il n'y a aucun moyen de connaître l'unité utilisée pour représenter un angle donné. Dès lors, il est très important de toujours avoir en tête, lorsqu'on écrit du code manipulant des angles, l'unité dans laquelle ils sont exprimés. En effet, les erreurs d'unités peuvent avoir des conséquences fâcheuses1.
Dès lors, nous adopterons la convention suivante : dans la mesure du possible, tous les angles du projet seront représentés en radians. Lorsqu'un angle doit être représenté dans une autre unité, celle-ci sera rappelée au moyen d'un suffixe dans le nom de la variable ou méthode concernée : deg pour les angles exprimés en degrés, hr pour ceux exprimés en heures. Pensez à suivre cette convention dans votre code pour le rendre plus facile à comprendre et éviter les erreurs !
Le fait que nous ayons choisi de représenter les angles par de simples valeurs de type double implique qu'il n'existe pas de classe représentant un angle. Il est toutefois utile d'avoir à disposition des méthodes de manipulation d'angles, et nous n'avons pas d'autre choix, en Java, que de les placer dans une classe, sous forme de méthodes statiques.
Cette classe est la classe Angle du paquetage ch.epfl.rigel.math, et elle est publique, finale et non instanciable. Son seul but est, comme dit ci-dessus, de regrouper les méthodes et constantes permettant de travailler sur des angles représentés par des valeurs de type double.
Cette classe définit la constante publique, finale et statique suivante :
double TAU, qui représente la constante τ.
De plus, elle offre les méthodes publiques et statiques suivantes :
double normalizePositive(double rad), qui normalise l'angleraden le réduisant à l'intervalle [0,τ[,double ofArcsec(double sec), qui retourne l'angle correspondant au nombre de secondes d'arc donné, qui peut être quelconque (y compris négatif),double ofDMS(int deg, int min, double sec), qui retourne l'angle correspondant à l'angledeg°min′sec″, ou lèveIllegalArgumentExceptionsi les minutes données ne sont pas comprises entre 0 (inclus) et 60 (exclus), ou si les secondes ne sont pas comprises entre 0 (inclus) et 60 (exclus),double ofDeg(double deg), qui retourne l'angle correspondant à l'angle en degrés donné,double toDeg(double rad), qui retourne l'angle en degrés correspondant à l'angle donné,double ofHr(double hr), qui retourne l'angle correspondant à l'angle en heures donné,double toHr(double rad), qui retourne l'angle en heures correspondant à l'angle donné.
3.6.1 Conseils de programmation
La plupart des méthodes de la classe Angle sont triviales à écrire et tiennent en une ligne. Toutefois, il est important de les écrire de manière à ce qu'une personne lisant le code puisse être immédiatement persuadée qu'elles sont correctes.
Pour ce faire, nous vous conseillons de procéder ainsi pour chaque méthode de conversion :
- définir une constante « évidemment correcte » donnant le nombre d'unités destination par unité source,
- écrire la méthode de conversion au moyen d'une simple multiplication par cette constante.
Cette idée peut être illustrée avec la conversion de radians vers degrés. Pour commencer, définissons la constante donnant le nombre de degrés par radians :
private static final double DEG_PER_RAD = 360.0 / TAU;
Cette définition est « évidemment correcte » car la division ne fait rien d'autre que diviser la longueur d'un tour exprimé en degrés (360°) par sa longueur exprimée en radians (τ).
Une fois cette constante définie, la méthode de conversion de radians en degrés s'exprime au moyen d'une simple multiplication :
public static double toDeg(double rad) {
return rad * DEG_PER_RAD;
}
Là aussi, cette définition est « évidemment correcte » car on multiplie des radians par des degrés divisés par des radians, et le résultat est donc en degrés.
Cela dit, cette conversion-ci se fait encore plus simplement en appelant la méthode toDegrees de la classe Math, et c'est donc ce que vous devez faire ! Néanmoins, la technique illustrée ci-dessus s'applique à plusieurs autres méthodes de conversion de la classe Angle.
Sachez pour terminer que la classe Math du paquetage java.lang contient, en plus de toDegrees, d'autres méthodes et constantes qui sont très utiles ici, parmi lesquelles la constante PI et la méthode toRadians.
3.7 Classe Polynomial
La classe Polynomial du paquetage ch.epfl.rigel.math, publique, finale et immuable, représente une fonction polynomiale.
Son constructeur est privé, mais elle offre une méthode de construction publique et statique :
Polynomial of(double coefficientN, double... coefficients), qui retourne la fonction polynomiale avec les coefficients donnés, ordonnés par degré en ordre décroissant, ou lève l'exceptionIllegalArgumentExceptionsi le coefficient de plus haut degré (coefficientN) vaut 0.
Étant donné que les coefficients sont passés à la méthode of par ordre décroissant, l'appel suivant :
Polynomial.of(4, -1, 0, 2);
retourne l'objet représentant la fonction polynomiale suivante : \[ 4\,x^3 - x^2 + 2 \] En d'autres termes, le dernier coefficient est toujours celui de degré 0, l'avant-dernier celui de degré 1, et ainsi de suite.
La raison pour laquelle le premier coefficient (coefficientN) est passé séparément des autres est simplement que cela rend impossible l'appel de cette méthode avec 0 arguments, ce qui serait incorrect. Cette petite astuce est souvent utilisée en Java pour définir des méthodes acceptant un nombre variable mais non nul d'arguments, et il est bon de la connaître.
Il faut toutefois noter que même si les coefficients sont passés à la méthode of au moyen d'une paire d'arguments — coefficientN, de type double, et coefficients, de type double[] —, ils doivent être stockés dans un tableau unique par la classe Polynomial.
En plus de la méthode de construction susmentionnée, Polynomial offre la méthode publique suivante :
double at(double x), qui retourne la valeur de la fonction polynomiale pour l'argument donné. Attention : pour des raisons de performance, cette valeur doit impérativement être calculée au moyen de la forme de Horner, sans aucune élévation à la puissance.
De plus, la classe Polynomial redéfinit la méthode toString de Object pour qu'elle retourne la représentation textuelle de la fonction polynomiale. Cette chaîne doit être minimale, dans le sens où elle ne doit pas inclure de coefficient, exposant ou signe superflu. Cette contrainte complique quelque peu sa mise en œuvre, mais constitue un excellent exercice de programmation.
Finalement, la classe Polynomial redéfinit les méthodes hashCode et equals pour qu'elles lèvent l'exception UnsupportedOperationException.
3.7.1 Conseils de programmation
Comme expliqué ci-dessus, la méthode of doit collecter la totalité des coefficients dans un nouveau tableau, qui constitue l'unique attribut de la classe Polynomial. Pour effectuer la copie des éléments du tableau reçu dans le nouveau, la méthode arraycopy de la classe System est utile — et efficace, même si cela n'est pas très important ici. Notez que même si les coefficients étaient passés dans un seul tableau, celui-ci devrait être copié avant stockage, pour garantir l'immuabilité de la classe.
Pour construire la chaîne retournée par toString, il est conseillé d'utiliser la classe StringBuilder, qui est un bâtisseur de chaînes de caractères.
3.8 Tests
Pour vous aider à démarrer ce projet, nous vous fournissons exceptionnellement une archive Zip contenant des tests unitaires JUnit pour cette étape.
Pour pouvoir utiliser ces tests, il vous faut :
3.9 Documentation
Une fois les tests exécutés avec succès, il vous reste à documenter la totalité des entités publiques (classes, attributs et méthodes) définies dans cette étape, au moyen de commentaires Javadoc, comme décrit dans le guide consacré à ce sujet. Vous pouvez écrire ces commentaires en français ou en anglais, en fonction de votre préférence, mais vous ne devez utiliser qu'une seule langue pour tout le projet.
4 Résumé
Pour cette étape, vous devez :
- installer la version 11 (et ni une plus récente, ni une plus ancienne !) de Java sur votre ordinateur, ainsi que la dernière version d'IntelliJ ou d'Eclipse,
- si vous utilisez Eclipse, le configurer selon les indications données dans le document consacré à ce sujet,
- écrire les classes
Preconditions,Interval,ClosedInterval,RightOpenInterval,AngleetPolynomialselon les indications données plus haut, - vérifier que les tests que nous vous fournissons s'exécutent sans erreur, et dans le cas contraire, corriger votre code,
- documenter la totalité des entités publiques que vous avez définies,
- (optionnel mais fortement recommandé) rendre votre code au plus tard le 21 février 2020 à 17h00, via le système de rendu.
Ce premier rendu n'est pas noté, mais celui de la prochaine étape le sera. Dès lors, il est vivement conseillé de faire un rendu de test cette semaine afin de se familiariser avec la procédure à suivre.
Notes de bas de page
Ainsi, en 1999, la sonde spatiale Mars Climate Orbiter de la NASA a été détruite car deux parties de son logiciel de contrôle utilisaient des unités différentes et les ingénieurs avaient oublié d'en tenir compte. Pour éviter ce genre d'erreurs, certains langages de programmation — p.ex. F# de Microsoft — permettent de représenter les unités des valeurs manipulées. Malheureusement, ces langages sont encore trop peu nombreux, et Java n'est pas l'un d'eux.