Images continues
Série 2
Introduction
Cette série a pour thème les images, représentées de manière inhabituelle.
D'habitude, en informatique, les images sont représentées par un tableau bidimensionnel d'échantillons de couleur, appelés pixels (pour picture elements). Nous qualifierons cette représentation classique des images de discrète et finie puisque la couleur de l'image n'est connue qu'en un nombre fini de points.
La représentation que nous utiliserons ici est quant à elle continue et infinie. La mémoire d'un ordinateur étant finie, il n'est bien entendu pas possible de représenter directement une telle image par l'ensemble (infini) de ses pixels. Au lieu de cela, on utilise la technique habituellement utilisée en mathématiques, c-à-d qu'on représente une infinité de valeurs au moyen d'une fonction dont la représentation est, elle, finie.
Par exemple, la fonction mathématique \(f(x) = x^2\), dont la représentation est finie, est composée d'une infinité de paires de valeurs \((x, f(x))\), parmi lesquelles figurent p.ex. (0, 0), (1/2, 1/4) ou encore (12.3, 151.29).
De même, une image peut être vue comme une fonction à deux variables, les coordonnées x et y d'un point du plan, dont la valeur est une couleur. Par exemple, la fonction suivante est une image d'un disque rouge sur fond blanc, centré à l'origine et de rayon 1 : \[ f(x, y) = \begin{cases} \color{red}\blacksquare \text{ (rouge)} & \text{si } \sqrt{x^2 + y^2} \le 1\\ \color{white}\blacksquare \text{ (blanc)} & \text{sinon} \end{cases} \]
On peut traduire cette idée en Java en définissant une interface pour le concept d'image continue. Cette interface ne contient qu'une seule méthode abstraite, qui associe une couleur à chaque point du plan :
public interface ImageRGB {
public ColorRGB apply(float x, float y);
}
ColorRGB représente une couleur, identifiée par le triplet de ses composantes rouges, vertes et bleues (abrégé RGB pour red, green et blue), chacune comprises entre 0 et 1. La valeur 0 représente l'absence d'une composante, tandis que la valeur 1 représente la « présence maximale » de cette composante.
Une fois l'interface ImageRGB définie, il est possible d'écrire une classe l'implémentant, nommée RedDisk et représentant le disque sur fond blanc donné plus haut :
public final class RedDisk implements ImageRGB {
@Override
public ColorRGB apply(float x, float y) {
double r = Math.sqrt(x * x + y * y);
return r <= 1.0 ? ColorRGB.RED : ColorRGB.WHITE;
}
}
ColorRGB.RED et ColorRGB.WHITE sont simplement des constantes prédéfinies pour les couleurs (1, 0, 0) et (1, 1, 1), respectivement.
Cela fait, on peut encore ajouter un attribut statique à la classe RedDisk, contenant une instance de la classe.
public final class RedDisk implements ImageRGB {
public static final ImageRGB IMAGE = new RedDisk();
// … reste comme ci-dessus
}
En affichant à l'écran l'image contenue dans RedDisk.IMAGE, au moyen du programme fourni plus bas, on obtient bien ce à quoi on s'attend :

Figure 1 : Le disque rouge unitaire sur fond blanc
Notez que l'on ne représente ici qu'une portion de l'image complète, puisqu'elle est infinie. Cette portion est comprise entre –1.5 et +1.5 pour chacune des coordonnées. Le repère utilisé est donc celui illustré ci-dessous :
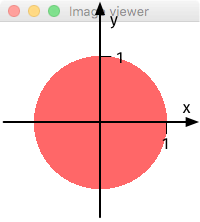
Figure 2 : Repère des images continues
Exercice 1
Créez un nouveau projet Eclipse pour cette série, puis importez-y le contenu de l'archive Zip que nous vous fournissons. Cette archive contient la définition de l'interface ImageRGB, la classe ColorRGB et un programme principal Main qui affiche une image à l'écran. En l'état, l'image qu'il affiche est celle du disque ci-dessus.
Prenez un petit moment pour vous familiariser avec la classe ColorRGB (vous pouvez ignorer tout ce qui est lié au gamma encodage). Jetez aussi un œil à la classe Main afin de trouver l'endroit, signalé par un commentaire, où l'image à afficher est créée. Vous devrez modifier l'expression de création d'image tout au long de cette série.
Une fois cela fait, et en vous inspirant de RedDisk, ajoutez à l'interface ImageRGB une seconde classe l'implémentant, nommée Chessboard et représentant un échiquier à cellules carrées du genre de celui-ci :

Figure 3 : Un échiquier aux cases noires et blanches, de largeur unitaire
Notez que la méthode floor de la classe java.lang.Math peut vous être utile. De plus, si la définition d'un échiquier ne vous paraît pas évidente, commencez par définir une image composée uniquement de bandes verticales noires et blanches de largeur unitaire. Cela devrait vous mettre sur la bonne piste.
Initialement, utilisez des valeurs fixes pour la largeur des cases (p.ex. 1) et la couleur des deux types de cases (p.ex. blanc et noir). Une fois que vous obtenez l'image attendue, modifiez votre classe pour que ces paramètres soient passés à son constructeur, et que celui-ci lève une exception si la largeur donnée n'est pas strictement positive.
Exercice 2
La notion d'image décrite plus haut, représentée par l'interface ImageRGB, peut être généralisée de manière intéressante : plutôt que de considérer qu'une image est une fonction associant une couleur à chaque point du plan, on peut considérer qu'il s'agit d'une fonction leur associant une donnée quelconque.
Cette généralisation permet, par exemple, de définir des « images » associant un nombre réel entre 0 et 1 à chaque point du plan. De telles images, appelées canal alpha dans des logiciels comme Photoshop, sont par exemple utiles pour mélanger deux images entre elles, comme nous le verrons à l'exercice suivant.
En Java, la généralisation de l'interface ImageRGB se fait naturellement au moyen de la généricité ! La nouvelle version de l'interface ImageRGB, renommée pour l'occasion en Image, ressemble à ceci :
public interface Image<T> {
public T apply(float x, float y);
}
Incorporez cette idée à votre programme en rendant l'interface ImageRGB générique, et en remplaçant toutes les utilisations de ce qui était ImageRGB par le type équivalent, à savoir Image<ColorRGB>. Notez que cela implique de modifier, de manière simple, la classe Main fournie.
Une fois cette modification faite, et après avoir vérifié que le programme fonctionne encore correctement, lisez le code de la classe Mysterious ci-dessous, qui définit une image générique à partir d'une autre image générique. Essayez de percer son mystère en comprenant ce qu'elle fait !
public final class Mysterious<T> implements Image<T> {
private final Image<T> image;
public Mysterious(Image<T> image) {
this.image = image;
}
@Override
public T apply(float x, float y) {
return image.apply(x * 2, y);
}
}
En fonction du résultat de vos réflexions, imaginez à quoi l'image ci-dessous devrait ressembler :
Image<ColorRGB> mysteriousRedDisk = new Mysterious<>(RedDisk.IMAGE);
Incluez maintenant ces deux définitions dans votre projet et vérifiez que l'image que vous obtenez correspond bien à vos attentes. Si ce n'est pas le cas, comprenez pourquoi avant de continuer !
En vous inspirant de la classe Mysterious, écrivez maintenant une classe Rotated du même genre, qui permette de tourner une image d'un certain angle, dans le sens antihoraire. Appliquée à un angle de 10° et à l'image de l'échiquier, cette classe devrait vous permettre d'obtenir l'image ci-dessous :

Figure 4 : L'échiquier de la figure 3 tourné de 10°
Si vous ne vous souvenez plus des formules à utiliser pour effectuer une rotation, consultez la page Wikipedia à ce sujet.
Exercice 3
Comme expliqué à l'exercice précédent, la notion généralisée d'image permet de définir ce que certains logiciels nomment un canal alpha (alpha channel) et que nous nommerons un masque. Un masque n'est rien d'autre qu'une image dont les valeurs sont un nombre réel compris entre 0 et 1.
La fonction ci-dessous, que nous appellerons masque dégradé horizontal pour des raisons qui deviendront claires plus tard, est un exemple de masque :
\[ f(x, y) = \begin{cases} 0 & \text{si }x \lt -1\\ 1 & \text{si }x \gt +1\\ \frac{x + 1}{2} & \text{sinon} \end{cases} \]
Définissez ce masque dans une classe nommée HorizontalGradientMask implémentant l'interface Image, instanciée comme il se doit.
Cela fait, définissez une dernière classe, nommée Composed, qui permette de composer deux images colorées, l'arrière-plan et l'avant-plan, au moyen d'un masque, pour produire une image finale. Dans cette image finale, la couleur de chaque point est obtenue en mélangeant la couleur de l'arrière-plan avec celle de l'avant-plan, selon la proportion donnée par le masque.
Par exemple, admettons qu'en un point P, l'arrière-plan soit rouge (1, 0, 0), l'avant-plan noir (0, 0, 0) et le masque égal à 0.2. Dès lors, l'image composée en ce point P a une couleur égale à un mélange de 80% de rouge et 20% de noir, soit (0.8, 0, 0).
Notez que ce mélange de couleurs peut se faire très simplement au moyen de la méthode mixWith de la classe ColorRGB fournie.
En utilisant cette classe de composition pour mélanger le disque rouge sur fond blanc (arrière-plan) avec l'échiquier tourné de la figure 4 (avant-plan) au moyen du masque dégradé horizontal, vous devriez obtenir l'image ci-dessous.

Figure 5 : L'échiquier masqué