Vecteurs de bits
Gameboj – Étape 7

Cette étape est la première de la seconde partie du projet, durant laquelle vous serez plus libres et moins guidés que durant la première. En particulier, vous avez maintenant le droit de modifier ou augmenter l'interface publique des classes et interfaces proposées, pour peu bien entendu que vous ayez une bonne raison de le faire. De plus, nous nous attendons à ce que vous lisiez et compreniez la documentation des parties de la bibliothèque Java que vous devez utiliser.

1 Introduction

Le but de cette étape est d'écrire une classe représentant les vecteurs de bits de taille (presque) quelconque. Elle sera utile pour représenter les images affichées sur l'écran du Game Boy, sujet de l'étape suivante.

Afin de comprendre l'utilité de cette classe, une rapide introduction à la représentation des images du Game Boy s'impose.

1.1 Images Game Boy

L'écran du Game Boy est capable d'afficher une image de 160 par 144 pixels en 4 teintes de gris — noir, gris foncé, gris clair ou blanc. D'après les standards actuels, une telle image est très petite (et peu colorée), comme l'illustre la copie d'écran du jeu Super Mario Land ci-dessous.

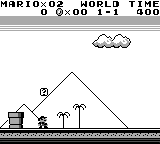
Figure 1 : Super Mario Land en résolution réelle

L'image affichée à l'écran n'est toutefois qu'une petite portion d'une image carrée de 256 pixels de côté, stockée dans une partie de la mémoire du Game Boy que l'on nomme la mémoire graphique. La figure ci-dessous montre à quoi ressemble l'image complète présente dans la mémoire graphique lorsque l'image ci-dessus est affichée à l'écran. La zone invisible à l'écran est teintée en bleu pour faciliter son identification.

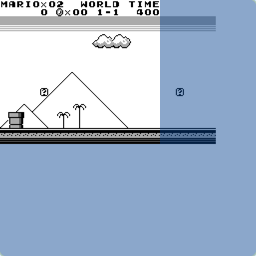
Figure 2 : Contenu de la mémoire vidéo pour l'image de la figure précédente

En comparant les deux images, on constate que le personnage de Mario manque sur la seconde. Cela est dû au fait qu'il est dessiné séparément, au moyen de ce que l'on nomme un sprite, notion qui sera décrite dans une étape ultérieure.

La raison pour laquelle l'écran du Game Boy n'affiche qu'une petite portion d'une image stockée en mémoire est que cela facilite la réalisation de certains effets. Par exemple, pour faire défiler le paysage lorsque le personnage de Mario se déplace, il suffit — dans un premier temps en tout cas — de changer la portion de l'image affichée à l'écran. Cela peut se faire par une simple modification d'un registre du contrôleur d'écran, comme nous le verrons plus tard.

1.2 Représentation des images dans le simulateur

Dans le simulateur, nous représenterons les images du Game Boy par une liste de lignes. Chaque ligne sera composée soit de 256 pixels — si l'image dont elle fait partie est celle stockée en mémoire — soit de 160 pixels — si l'image dont elle fait partie est celle affichée à l'écran.

Etant donné que l'écran n'est capable d'afficher que quatre couleurs, deux bits suffisent pour représenter la couleur d'un pixel. Dès lors, une ligne d'une image de 256 pixels peut être représentée au moyen de 512 bits, tandis qu'une ligne d'une image de 160 pixels peut l'être au moyen de 320 bits.

La question qui se pose est de savoir comment organiser ces bits en mémoire. La solution la plus naturelle serait probablement de placer côte à côte les 2 bits d'un pixel donné. Toutefois, sur le Game Boy, une organisation différente est utilisée, et nous nous en inspirerons pour notre simulateur. Elle consiste à stocker séparément les bits de poids fort et les bits de poids faible de chaque pixel.

Cette organisation est illustrée par la figure ci-dessous, qui montre la représentation d'une ligne composée de 4 pixels dont la couleur est — de gauche à droite — 0 (blanc), 1 (gris clair), 2 (gris foncé) et 3 (noir). Les 8 bits nécessaires à la représentation de la couleur de chacun des 4 pixels sont séparés en deux vecteurs de 4 bits chacun : MSB (pour most-significant bits) contient les bits de poids fort, tandis que LSB (pour least-significant bits) contient ceux de poids faible.

Figure 3 : Représentation d'une ligne de 4 pixels de couleur 0, 1, 2 et 3

Comme nous le verrons ultérieurement, nous ajouterons généralement un troisième vecteur de bits aux deux contenant les bits de poids faible et de poids fort. Ce troisième vecteur contiendra l'opacité de chacun des pixels, et sera utile pour superposer deux images.

En conclusion, une image du Game Boy sera représentée dans notre simulateur par une liste de lignes, chacune d'entre elles étant constituée d'une paire ou d'un triplet de vecteurs de 256 ou 160 bits. En conséquence, il importe de savoir comment représenter de tels vecteurs de bits.

1.3 Vecteurs de bits de taille variable

Les vecteurs de bits utilisés jusqu'à présent dans ce projet avaient une taille de 8, 16 ou 32 bits. Ils pouvaient donc très facilement être représentés au moyen du type int de Java qui, pour mémoire, est un vecteur de 32 bits.

Malheureusement, ni le type int, ni même le type long (64 bits) de Java ne suffisent pour représenter directement un vecteur de 256 ou 160 bits. Il faut donc trouver comment représenter de tels vecteurs de plus grande taille, et c'est le but de cette étape.

L'idée consiste simplement à utiliser un tableau de valeurs de type int pour représenter un vecteur de n bits, chaque élément du tableau contenant donc 32 bits. Pour faciliter les choses, nous ferons l'hypothèse que n est toujours un multiple de 32, ce qui se trouve être le cas des vecteurs de 256 (32×8) et 160 (32×5) bits qui nous intéressent.

La plupart des opérations dont nous aurons besoin sur ces vecteurs sont classiques et correspondent aux opérateurs fournis par Java : complément (~), conjonction (&), disjonction (|), décalage (<< et >>), etc. Une opération importante, que nous nommerons extraction généralisée, échappe toutefois à cette règle et mérite d'être décrite en détail.

1.3.1 Extraction généralisée

Comme son nom l'indique, l'extraction généralisée est une généralisation de l'opération d'extraction « normale » décrite à l'étape 1 et mise en œuvre — pour les vecteurs de 32 bits — par la méthode extract de la classe Bits.

L'opération d'extraction « normale » exige que les index des bits qu'on lui demande d'extraire soient compris entre 0 et la taille du vecteur (exclue). Par exemple, la méthode extract de Bits lève une exception si on lui passe une valeur négative comme index de départ (start).

L'idée de l'extraction généralisée est de supprimer cette contrainte, en considérant que les bits à extraire proviennent d'un vecteur de longueur infinie, obtenu à partir du vecteur sur lequel on désire effectuer l'extraction, et appelé son extension (infinie). La question qui se pose est de savoir comment calculer cette extension.

On peut imaginer de nombreuses manières de calculer l'extension infinie d'un vecteur, mais pour ce projet nous n'en aurons besoin que de deux :

l'extension par 0, qui consiste à étendre le vecteur original en ajoutant un nombre infini de 0 à sa gauche et à sa droite,
l'extension par enroulement, qui consiste à étendre le vecteur original en lui ajoutant un nombre infinie de copies de lui-même à sa gauche et à sa droite.

Ces deux techniques d'extensions peuvent s'illustrer au moyen d'un exemple. Soit un vecteur de 4 bits, abcd, où a, b, c et d sont les bits individuels :

Bit	3	2	1	0
Valeur	`a`	`b`	`c`	`d`

L'extension par 0 de ce vecteur est un vecteur infini valant :

Bit	…	5	4	3	2	1	0	-1	-2	…
Valeur	`0`	`0`	`0`	`a`	`b`	`c`	`d`	`0`	`0`	`0`

tandis que l'extension par enroulement est un vecteur infini valant :

Bit	…	5	4	3	2	1	0	-1	-2	…
Valeur	…	`c`	`d`	`a`	`b`	`c`	`d`	`a`	`b`	…

L'extraction généralisée consiste (conceptuellement en tout cas) à extraire des vecteurs de bits de taille finie de ces extensions infinies. Par exemple, en extrayant le sous-vecteur de 4 bits commençant au bit d'index -2 de l'extension par 0 ci-dessus, on obtient :

Bit	3	2	1	0
Valeur	`c`	`d`	`0`	`0`

tandis qu'en extrayant le même sous-vecteur de l'extension par enroulement, on obtient :

Bit	3	2	1	0
Valeur	`c`	`d`	`a`	`b`

Notez que le premier de ces deux vecteurs est aussi celui qu'on obtient en effectuant un décalage à gauche de 2 bits du vecteur original, tandis que le second est celui qu'on obtient en effectuant une rotation à gauche de 2 bits ! L'extraction généralisée peut donc également être vue comme une généralisation des opérations de décalage et de rotation.

2 Mise en œuvre Java

A partir de cette étape, la mise en œuvre Java est moins guidée qu'auparavant. En particulier, l'interface publique des classes et interfaces est décrite de manière plus succincte.

Les noms des classes, interfaces et méthodes donnés ne sont dorénavant que des propositions, libre à vous d'en choisir d'autres. Cela dit, afin de ne pas compliquer inutilement le processus de correction, il vous est demandé de ne pas trop vous éloigner de la mise en œuvre que nous vous proposons.

2.1 Classe `BitVector`

La classe BitVector, du paquetage ch.epfl.gameboj.bits, publique, finale et immuable, représente un vecteur de bits dont la taille est un multiple de 32 strictement positif.

Cette classe offre deux constructeurs publics : le premier prend une taille (en bits) et une valeur initiale (sous forme d'un booléen) et construit un vecteur de bits de la taille donnée, dont tous les bits ont la valeur donnée ; le second ne prend qu'une taille en argument et initialise tous les bits à 0. Ces deux constructeurs lèvent une exception si la taille n'est pas un multiple de 32 strictement positif.

De plus, la classe BitVector offre des méthodes publiques permettant de :

connaître la taille du vecteur, en bits (size),
déterminer si le bit d'index donné est vrai ou faux (testBit),
calculer le complément du vecteur de bits (not),
calculer la conjonction et la disjonction bit à bit avec un autre vecteur de même taille (and, or),
extraire un vecteur de taille donnée de l'extension par 0 du vecteur (extractZeroExtended),
extraire un vecteur de taille donnée de l'extension par enroulement du vecteur (extractWrapped),
décaler le vecteur d'une distance quelconque, en utilisant la convention habituelle qu'une distance positive représente un décalage à gauche, une distance négative un décalage à droite (shift).

N'oubliez pas que cette classe est immuable, ce qui implique que les méthodes not, and, or, shift et les deux variantes de extract retournent un nouveau vecteur de bits.

Finalement, étant donné que la classe BitVector est immuable, elle redéfinit les méthodes equals et hashCode afin que ses instances soient comparées de manière structurelle. En d'autres termes, deux vecteurs de bits sont considérés comme égaux si et seulement si ils ont la même taille et leurs bits sont égaux deux à deux.

Il est également conseillé de redéfinir la méthode toString, qui peut p.ex. retourner une représentation du vecteur sous la forme d'une chaîne composée uniquement de caractères 0 et 1.

2.1.1 Exemple

L'exemple ci-dessous illustre l'utilisation de quelques méthodes de la classe BitVector, en admettant que les noms proposés plus haut aient été choisis :

BitVector v1 = new BitVector(32, true);
BitVector v2 = v1.extractZeroExtended(-17, 32).not();
BitVector v3 = v2.extractWrapped(11, 64);
for (BitVector v: List.of(v1, v2, v3))
  System.out.println(v);

En exécutant cet extrait de programme, les trois lignes ci-dessous, correspondant aux vecteurs v1 à v3, sont affichées sur la console :

11111111111111111111111111111111
00000000000000011111111111111111
1111111111100000000000000011111111111111111000000000000000111111

2.1.2 Conseils de programmation

Certains aspects de la classe BitVector ne sont pas évidents à mettre en œuvre, et quelques conseils vous sont donc donnés ci-après.

Constructeurs

En plus des deux constructeurs publics, il est conseillé d'en définir un privé, qui prenne en argument un tableau de type int[] contenant les éléments du vecteur, et qui se contente de le stocker — sans le copier — dans un attribut de l'instance. Ce constructeur facilite la définition des constructeurs publics, de nombreuses méthodes de la classe BitVector, ainsi que celle de la méthode build du bâtisseur décrit plus bas.
Classe Arrays

Plusieurs méthodes de la classe Arrays de la bibliothèque Java peuvent faciliter la mise en œuvre de la classe BitVector. En particulier, fill peut être utile dans l'un des constructeurs, tandis que hashCode et equals peuvent l'être dans les méthodes du même nom — mais de BitVector.
Méthodes d'extraction

L'écriture des méthodes d'extraction n'est pas triviale et demande de très bien réfléchir avant de commencer à programmer. Il est fortement conseillé de s'aider de dessins pour cela, qui facilitent beaucoup la compréhension.

Pour commencer, il est important de constater que les deux méthodes d'extraction sont quasi-identiques, seule change la manière dont l'extension infinie du vecteur est calculée. Dès lors, il est possible d'écrire une seule méthode d'extraction générale, privée et nommée p.ex. extract, prenant un argument supplémentaire décrivant le type d'extraction à effectuer. Elle peut ensuite être utilisée pour mettre en œuvre (trivialement) les deux méthodes d'extraction spécifiées plus haut.

Dans les grandes lignes, la méthode extract procède ainsi : elle crée un tableau de type int[] destiné à contenir les groupes de bits du vecteur résultant de l'extraction, remplit un à un les éléments de ce tableau, et finalement construit et retourne le vecteur dont les bits sont ceux du tableau. La plupart de ces opérations sont triviales, le principal problème étant de calculer les éléments du tableau.

Avant de considérer ce problème-là, posons-nous toutefois la question de savoir comment prendre en compte le fait que l'extraction se fait sur l'extension infinie du vecteur et pas sur le vecteur lui-même.

Une idée naïve serait de représenter effectivement cette extension infinie sous la forme d'un vecteur, mais cela n'est bien entendu pas possible car il faudrait avoir une quantité infinie de mémoire à disposition.

Une meilleure idée consiste à définir une méthode privée qui, étant donné le type d'extension désiré et un index, retourne l'élément du tableau de l'extension infine se trouvant à cet index. Notez bien que les éléments dont il est question ici sont des groupes de 32 bits représentés par des valeurs de type int.

Reste maintenant à déterminer comment effectuer l'extraction proprement dite. Avant de considérer le problème dans toute sa généralité, il est utile d'en considérer un cas particulier : celui dans lequel le premier bit à extraire a un index qui est un multiple de 32, p.ex. 0, 64 ou -32. Dans ce cas, chaque élément du tableau à remplir est simplement une copie d'un élément du tableau correspondant à l'extension infinie du vecteur original.

La figure ci-dessous illustre cela au moyen d'un exemple dans lequel un vecteur de 96 bits est extrait à partir du bit d'index -32 de l'extension par 0 d'un autre vecteur de 96 bits dont les 32 premiers bits sont désignés par A, les 32 suivants par B et les 32 derniers par C.

Figure 4 : Extraction d'un vecteur de 96 bits à partir du bit -32

Ce cas particulier mérite d'être traité séparément dans le code, d'une part car il peut être mis en œuvre de manière plus efficace que le cas général, et d'autre part car la définition du cas général s'en trouve simplifiée.

Le cas général est un peu plus complexe, mais pas beaucoup. Ce qu'il faut constater, c'est que lorsque le premier bit à extraire a un index qui n'est pas un multiple de 32, alors chaque élément du tableau s'obtient en combinant exactement deux éléments du tableau correspondant à l'extension infinie du vecteur original.

La figure ci-dessous illustre ce cas au moyen d'un exemple similaire au précédent mais où l'extraction se fait à partir du bit d'index -8.

Figure 5 : Extraction d'un vecteur de 96 bits à partir du bit -8

Il reste encore à savoir comment calculer l'index des deux éléments à combiner, ainsi que le décalage à appliquer à ces éléments avant de les combiner. Assez naturellement, ces valeurs s'obtiennent au moyen d'une division entière par 32, et de son reste, de l'index du premier bit à extraire. Attention toutefois : pour que les calculs soient corrects également avec les index négatifs, il est impératif d'utiliser les méthodes floorDiv et floorMod de la classe Math en lieu et place des opérateurs / et %.
Méthode de décalage

Une fois les méthodes d'extraction définies, la méthode de décalage (shift) est triviale à mettre en œuvre, et s'écrit en une ligne. En effet, comme nous l'avons vu plus haut, un décalage est équivalent à une extraction effectuée sur l'extension par 0 du vecteur.

2.2 Classe `BitVector.Builder`

La classe Builder, publique et finale, est imbriquée statiquement dans BitVector et représente un bâtisseur de vecteur de bits. Son but principal est de permettre la construction d'une vecteur de bits de manière incrémentale, octet par octet.

Le constructeur de la classe Builder prend en argument la taille du vecteur de bits à construire, qui doit être un multiple de 32 strictement positif. La totalité des bits du vecteur à construire valent initialement 0. En plus de ce constructeur, la classe Builder offre deux méthodes publiques permettant de :

définir la valeur d'un octet désigné par son index (setByte),
construire le vecteur de bits (build).

La méthode setByte lève IndexOutOfBoundsException si l'index de l'octet qu'on lui donne est invalide. De plus, elle retourne le bâtisseur afin de pouvoir chaîner les appels.

(La raison pour laquelle ce bâtisseur n'offre que la méthode setByte pour modifier les bits du vecteur en construction est que cela suffit aux besoins de ce projet. Il aurait bien entendu aussi été possible de définir d'autres méthodes permettant p.ex. de modifier les bits individuellement, ou alors 32 à la fois, etc.)

2.2.1 Exemple

L'exemple ci-dessous illustre l'utilisation du bâtisseur pour construire un vecteur de 32 bits :

BitVector v = new BitVector.Builder(32)
  .setByte(0, 0b1111_0000)
  .setByte(1, 0b1010_1010)
  .setByte(3, 0b1100_1100)
  .build();
System.out.println(v);

En exécutant cet extrait de programme, la ligne suivante est affichée sur la console :

11001100000000001010101011110000

2.2.2 Conseils de programmation

La méthode build doit appeler directement le constructeur privé de la classe BitVector en lui passant le tableau contenant les bits du vecteur en construction.

Pour mémoire, ce constructeur ne copie pas le tableau qu'on lui passe, pour des raisons de performance. Dès lors, pour garantir l'immuabilité de la classe BitVector, il faut s'assurer que l'utilisateur du bâtisseur n'ait plus la possibilité de modifier ce tableau une fois la méthode build appelée.

Cela implique que l'appel à la méthode build rende le bâtisseur invalide, et que tout appel ultérieur à setByte ou à build lève une exception — en général, IllegalStateException est utilisée dans cette situation.

Une technique simple pour mettre en œuvre ce comportement consiste à s'assurer que build stocke null dans l'attribut du bâtisseur contenant le tableau des bits du vecteur en construction, une fois celui-ci passé au constructeur de BitVector. Ensuite, setByte et build peuvent simplement détecter cette situation et lever une exception.

2.3 Tests

A partir de cette étape, aucun fichier de vérification de signatures ne vous est fourni, étant donné que la signature des différentes méthodes n'est plus spécifiée en détail.

Pour la même raison, aucun test unitaire ne sera plus fourni à l'avenir, à vous d'écrire les vôtres. Notez que cela est fortement recommandé en général, et en particulier pour cette étape-ci, car la classe BitVector est à la base de toute la partie graphique de ce projet. La moindre erreur dans l'une de ses méthodes provoquera des erreurs d'affichage dont l'origine sera très difficile à déterminer.

3 Résumé

Pour cette étape, vous devez :

écrire la classe BitVector (ou équivalent) en fonction des indications données plus haut,
tester votre code,
documenter la totalité des entités publiques que vous avez définies.

Aucun rendu n'est à faire pour cette étape avant le rendu final. N'oubliez pas de faire régulièrement des copies de sauvegarde de votre travail en suivant nos indications à ce sujet.

Vecteurs de bits Gameboj – Étape 7