Modèles HGT et profils altimétriques
Etape 4
1 Introduction
Le but de cette quatrième étape est d'écrire les classes représentant :
- un modèle numérique du terrain discret provenant d'un fichier binaire,
- un profil altimétrique.
Avant de décrire la mise en œuvre Java de ces deux classes, le format des fichiers binaires utilisés doit être présenté, de même que quelques notions liées aux profils altimétriques.
1.1 Fichiers HGT
Les modèles numériques du terrain que nous utiliserons pour ce projet sont stockés dans des fichiers binaires, dans un format nommé HGT (pour height).
Un fichier HGT couvre toujours une zone de 1° de côté en longitude et en latitude. Le nom du fichier donne les coordonnées, en degrés, du coin sud-ouest de cette zone. Par exemple, un fichier HGT nommé N46E007.hgt couvre la zone dont le coin sud-ouest a les coordonnées (+7°, +46°). Son coin nord-est a donc les coordonnées (+8°, +47°). L'image ci-dessous montre la zone couverte par ce fichier.
Figure 1 : Zone couverte par le fichier nommé N46E007.hgt
Un fichier HGT contient les altitudes d'un certain nombre de points séparés les uns des autres par une distance angulaire constante d'une seconde d'arc.
Un degré étant composé de 60 minutes d'arc, composées chacune de 60 secondes, un seul fichier contient l'altitude de (60 × 60 + 1)2 = 12 967 201 points. Le +1 dans cette formule provient du fait qu'il y a chevauchement entre les fichiers HGT voisins, chacun partageant une ligne avec son voisin du dessus, une avec son voisin du dessous, une colonne avec son voisin de gauche et une avec son voisin de droite. Les altitudes sont données en mètres, sous forme de valeurs entières occupant deux octets successifs.
La première altitude figurant dans un fichier HGT est celle de son coin haut-gauche (!). La seconde est celle de son voisin de droite, et ainsi de suite jusqu'à la fin de la première ligne. Viennent ensuite les altitudes de la seconde ligne, de gauche à droite, et ainsi de suite. Le point dont l'altitude figure en premier dans le fichier HGT de la figure ci-dessus est donc le point mis en évidence en rouge. Attention : ce point n'est pas celui qui donne son nom au fichier !
1.1.1 Fichiers fournis
Nous mettons à votre disposition une archive Zip contenant 18 fichiers HGT couvrant la zone allant de 6° à 12° de longitude, et de 45° à 48° de latitude. Cette archive est à importer dans votre projet comme d'habitude. La zone couverte par les fichiers qu'elle contient est illustrée ci-dessous.
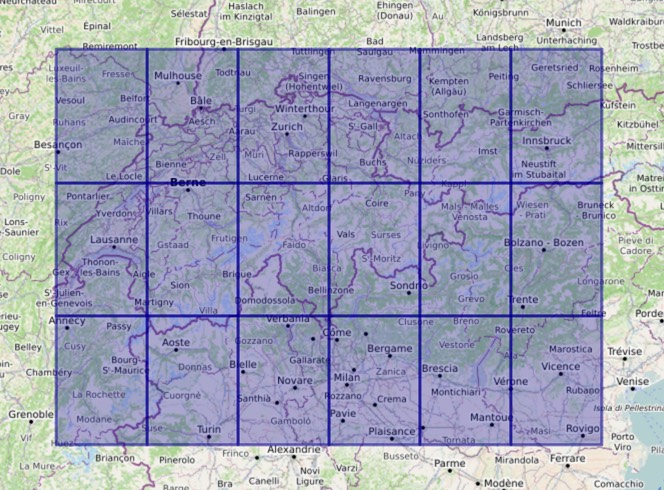
Figure 2 : Zone couverte par les fichiers fournis (carte OpenStreetMap)
Tous ces fichiers HGT proviennent du site Viewfinder Panoramas de Jonathan de Ferranti. Les personnes intéressées à en télécharger d'autres les trouveront sur la page de téléchargement.
1.2 Profil altimétrique
Un profil altimétrique donne l'altitude de la surface de la Terre le long d'un tracé déterminé. Par exemple, l'image ci-dessous représente le profil altimétrique de l'arc de grand cercle partant des Pierres du Niton à Genève et se terminant à la gare de la Chaux-de-Fonds. Il a été obtenu grâce à l'outil de mesure du site map.geo.admin.ch.
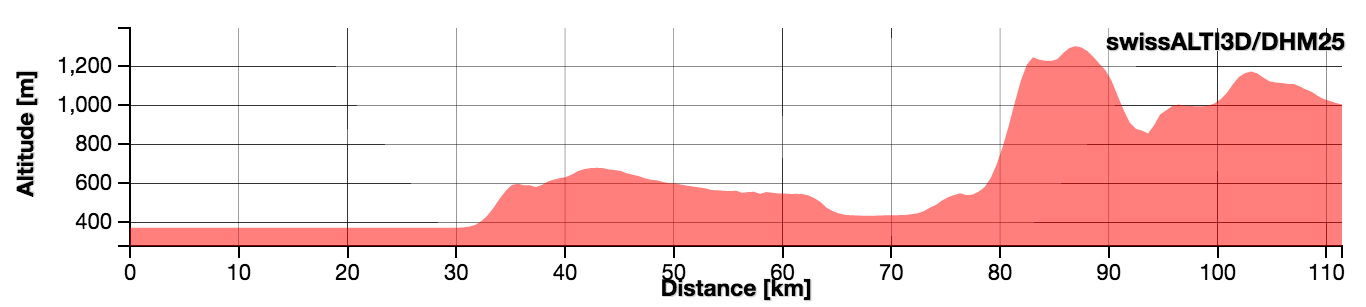
Figure 3 : Profil altimétrique (voir sur map.geo.admin.ch)
En termes mathématiques, un profil altimétrique est une fonction continue à une variable. Son argument est la distance depuis le point de départ, le long du tracé, et son résultat est l'altitude de la surface terrestre au point correspondant.
Dans le cas général, un profil altimétrique peut être établi le long d'un tracé quelconque, par exemple le long d'une route. Dans le cadre de ce projet, nous ne nous intéresserons toutefois qu'à un seul type de profil : ceux dont le tracé est un arc de grand cercle. Le profil ci-dessus est de ce type.
1.3 Coordonnées des points d'un grand cercle
Pour construire un profil altimétrique dont le tracé est un arc de grand cercle, il faut pouvoir calculer les coordonnées d'un point quelconque sur un tel arc.
Les formules ci-dessous permettent de déterminer les coordonnées \((\lambda, \varphi)\) du point situé à une distance de \(x\) radians (!) d'un point de coordonnées \((\lambda_O, \varphi_O)\), dans la direction \(\alpha\), le long d'un arc de grand cercle.
\begin{align*} \varphi &= \arcsin(\sin\varphi_O\,\cos x + \cos\varphi_O\,\sin x\,\cos \alpha)\\ \lambda &= \left[\lambda_O - \arcsin\left(\frac{\sin \alpha\,\sin x}{\cos\varphi}\right) + \pi\right] \bmod 2\pi - \pi \end{align*}Attention : dans ces formules, la distance \(x\) est en radians, pas en mètres, et la direction \(\alpha\) est donnée par ce que nous avons appelé un angle mathématique, pas un azimut.
Par exemple, admettons que l'on désire calculer les coordonnées du point situé à exactement 10240 mètres du point de coordonnées (6°, 46°), en direction du nord-est, correspondant à un azimut de 45°. On obtient :
\begin{align*} \sin\varphi_O &= \sin 46° \approx 0.71934\\ \cos\varphi_O &= \cos 46° \approx 0.69466\\ \sin x &\approx \sin 0.09209° \approx 0.00161\\ \cos x &\approx \cos 0.09209° \approx 1.00000\\ \sin \alpha &= \sin 315° \approx -0.70711\\ \cos \alpha &= \cos 315° \approx 0.70711\\ \varphi &\approx \arcsin(0.71934 + 0.00079) \approx 46.06508°\\ \arcsin\left(\frac{\sin a\,\sin x}{\cos\varphi}\right) &\approx -0.09385°\\ \lambda &\approx 6.09385° \end{align*}En d'autres termes, le point recherché a les coordonnées approximatives (6.09385°, 46.06508°).
2 Mise en œuvre Java
La mise en œuvre Java de cette étape consiste en deux classes, la première (HgtDiscreteElevationModel) représentant un MNT discret provenant d'un fichier HGT, la seconde (ElevationProfile) représentant un profil altimétrique. Toutes deux font partie du paquetage ch.epfl.alpano.dem.
2.1 Classe HgtDiscreteElevationModel
La classe HgtDiscreteElevationModel, publique et immuable (donc finale), représente un MNT discret obtenu d'un fichier au format HGT. Etant donné qu'elle représente un MNT discret, elle implémente l'interface DiscreteElevationModel.
Cette classe offre un unique constructeur public :
HgtDiscreteElevationModel(File file), qui construit un MNT discret dont les échantillons proviennent du fichier HGT passé en argument, ou lève l'exceptionIllegalArgumentExceptionsi le nom du fichier est invalide ou si sa longueur n'est pas celle attendue ; la classeFile, représentant un fichier, provient de la bibliothèque Java et est décrite plus bas.
Pour être valide, le nom d'un fichier HGT doit être composé de exactement 11 caractères, dont la signification est la suivante (dans l'ordre) :
- la lettre
N(pour north) ou la lettreS(pour south) indiquant si la latitude qui suit est positive (N) ou négative (S), - la latitude du coin sud-ouest, en degrés, exprimée avec 2 chiffres,
- la lettre
E(pour east) ou la lettreW(pour west) indiquant si la longitude qui suit est positive (E) ou négative (W), - la longitude du coin sud-ouest, en degrés, exprimée avec 3 chiffres,
- l'extension
.hgt.
Pour être valide, la longueur d'un fichier HGT doit être de 25 934 402 octets, étant donné qu'un tel fichier contient 12 967 201 échantillons d'altitude, occupant chacun 2 octets.
Les seules méthodes publiques offertes par HgtDiscreteElevationModel sont celles de l'interface DiscreteElevationModel.
Notez que pour charger les données du fichier HGT, cette classe doit utiliser une technique d'entrée/sortie particulière, désignée par l'anglicisme mappage, décrite à la section 2.1.3 ci-dessous.
2.1.1 Classe File
La classe File du paquetage java.io représente un fichier. Elle possède un certain nombre de méthodes permettant d'obtenir des informations sur le fichier, dont deux sont utiles à cette étape :
getName, qui retourne le nom du fichier sous forme de chaîne de caractères,length, qui retourne la longueur du fichier, en octets.
La classe File possède plusieurs constructeurs, mais le seul utile à cette étape est celui prenant le nom du fichier en argument, sous la forme d'une chaîne de caractères.
Notez qu'une instance de la classe File peut être passée à l'un des constructeurs de la classe FileInputStream pour créer un flot d'entrée d'octets pour ce fichier, comme l'illustre l'exemple de la section 2.1.4 ci-dessous.
2.1.2 Analyse du nom de fichier
2.1.3 Mappage de fichier
Le « mappage » d'un fichier en mémoire est une opération permettant — conceptuellement en tout cas — de charger d'un coup la totalité de son contenu en mémoire afin d'y accéder comme à un tableau, c'est-à-dire dans un ordre quelconque. Le mappage offre donc un accès aléatoire au contenu d'un fichier, contrairement aux flots qui y offrent un accès séquentiel.
Comparé à un véritable tableau contenant les octets d'un fichier, un fichier mappé en mémoire (memory mapped file) possède toutefois deux avantages importants :
- le contenu du fichier n'est lu que lorsque le programme l'utilise effectivement,
- les écritures faites en mémoire sont automatiquement répercutées sur le contenu du fichier stocké sur disque.
Le premier de ces deux avantages peut être intéressant pour ce projet, étant donné que les fichiers HGT sont gros mais que seul un petit sous-ensemble de leurs valeurs est généralement nécessaire pour le dessin d'un panorama donné.
Pour mapper un fichier en mémoire en Java, il faut tout d'abord obtenir un canal (de type FileChannel) pour ce fichier. Un moyen simple d'y parvenir consiste à d'abord obtenir un flot d'entrée sur le fichier, de type FileInputStream, puis d'utiliser la méthode getChannel de cette classe.
Une fois le canal obtenu, on peut utiliser sa méthode map pour mapper le fichier correspondant en mémoire. Cette méthode retourne un objet de type ByteBuffer qui représente (en gros) un tableau d'octets, ceux du fichier mappé.
Un tableau d'octet de type ByteBuffer peut être vu comme un tableau d'entiers de 16 bits de type ShortBuffer au moyen de sa méthode asShortBuffer, très utile ici étant donné que les fichiers HGT sont composés de tels entiers. Une fois cette vue obtenue, on peut l'utiliser pour lire un entier de 16 bits dont on connaît l'index au moyen de la méthode get.
2.1.4 Exemple
Le programme d'exemple suivant mappe en mémoire le fichier HGT nommé N46E007.hgt et en affiche les onze premières altitudes, lues sous la forme de valeurs de type short. Etant donné ce qui a été dit ci-dessus, ces valeurs sont les altitudes des points aux coordonnées :
Tous ces points se trouvant dans le lac de Neuchâtel, et ce dernier étant à une altitude de 429 m, cette valeur est imprimée onze fois par le programme.
import java.io.File;
import java.io.IOException;
import java.io.FileInputStream;
import java.nio.ShortBuffer;
import java.nio.channels.FileChannel.MapMode;
public class MemMapExample {
public static void main(String[] args)
throws IOException {
File f = new File("N46E007.hgt");
long l = f.length();
try (FileInputStream s = new FileInputStream(f)) {
ShortBuffer b = s.getChannel()
.map(MapMode.READ_ONLY, 0, l)
.asShortBuffer();
for (int i = 0; i <= 10; ++i)
System.out.println(b.get(i));
}
}
}
2.2 Classe ElevationProfile
La classe ElevationProfile, publique et immuable (donc finale), représente un profil altimétrique suivant un arc de grand cercle. Elle est dotée d'un unique constructeur public :
ElevationProfile(ContinuousElevationModel elevationModel, GeoPoint origin, double azimuth, double length), qui construit un profil altimétrique basé sur le MNT donné et dont le tracé débute au pointorigin, suit le grand cercle dans la direction donnée parazimuth, et a une longueur delengthmètres ; lève l'exceptionIllegalArgumentExceptionsi l'azimuth n'est pas canonique, ou si la longueur n'est pas strictement positive ; lève l'exceptionNullPointerExceptionsi l'un des deux autres arguments estnull.
En plus de ce constructeur, la classe ElevationProfile offre les méthodes publiques suivantes :
double elevationAt(double x), qui retourne l'altitude du terrain à la position donnée du profil, ou lève l'exceptionIllegalArgumentExceptionsi cette position n'est pas dans les bornes du profil, c-à-d comprise entre 0 et la longueur du profil,GeoPoint positionAt(double x), qui retourne les coordonnées du point à la position donnée du profil, ou lève l'exceptionIllegalArgumentExceptionsi cette position n'est pas dans les bornes du profil,double slopeAt(double x), qui retourne la pente du terrain à la position donnée du profil, ou lève l'exceptionIllegalArgumentExceptionsi cette position n'est pas dans les bornes du profil.
2.2.1 Interpolation de la position
Les méthodes elevationAt, slopeAt et positionAt doivent toutes trois calculer les coordonnées (longitude et latitude) d'un point à une position donnée du profil. Pour ce faire, elles pourraient bien entendu appliquer simplement les formules données à la section 1.3.
Malheureusement, ces formules sont assez coûteuses à calculer, car elles utilisent un grand nombre de fonction trigonométriques. Ce coût ne serait pas perceptible par l'utilisateur final si les méthodes susmentionnées n'étaient utilisées que rarement par le programme. Malheureusement, comme nous le verrons plus tard, tel n'est pas le cas. Par exemple, le dessin du panorama donné en exemple dans le document d'introduction au projet nécessite plus de 20 millions d'appels à la méthode positionAt.
Dès lors, il peut être utile d'optimiser ces méthodes. Une manière simple de le faire consiste à utiliser les formules de la section 1.3 pour calculer une fois pour toutes, à la construction d'un profil, la position d'un certain nombre de points régulièrement espacés (p.ex. tous les 4 km environ) le long de la trajectoire du grand cercle correspondant, puis d'interpoler linéairement entre ces positions par la suite.
Par exemple, imaginons qu'une instance de ElevationProfile soit construite ainsi :
ContinuousElevationModel dem = …; GeoPoint origin = new GeoPoint(toRadians(6), toRadians(46)); double azimuth = toRadians(45); double length = 100_000; ElevationProfile profile = new ElevationProfile(dem, origin, azimuth, length);
Le constructeur de ElevationProfile calcule, au moyen des formules de la section 1.3, la position (longitude et latitude) de points régulièrement espacés de 4096 m les uns des autres. Etant donné que la longueur du profil est de 100 km, il y en a 26. La table ci-dessous donne la position des quatre premiers et du dernier point ainsi calculés :
| Id | x (m) | Lon (°) | Lat (°) |
|---|---|---|---|
| 0 | 0 | 6.00000 |
46.00000 |
| 1 | 4096 | 6.03751 |
46.02604 |
| 2 | 8192 | 6.07506 |
46.05207 |
| 3 | 12288 | 6.11265 |
46.07809 |
| … | … | … | … |
| 25 | 102400 | 6.94857 |
46.64729 |
Une fois ces valeurs calculées et stockées, la méthode positionAt — qui est aussi appelée par elevationAt et slopeAt — les utilise pour déterminer, par interpolation linéaire, la position des points intermédiaires. Par exemple, pour l'appel suivant :
double e = profile.elevationAt(10240);
le résultat est calculé par interpolation linéaire entre les positions des points d'index 2 et 3, étant donné que 10240 se trouve entre 8192 et 12288. Comme 10240 se trouve exactement au milieu de 8192 et 12288, les coordonnées sont déterminées ainsi par l'interpolation :
\begin{align*} \varphi &= \tfrac{1}{2}(6.07506 + 6.11265) \approx 6.09386\\ \lambda &= \tfrac{1}{2}(46.05207 + 46.07809) \approx 46.06508\\ \end{align*}Comme on peut le voir en comparant ces valeurs à celles obtenues au moyen des formules exactes à la section 1.3, l'erreur introduite par l'interpolation est très faible, de l'ordre du mètre.
Notez que l'espacement des points choisi, 4096 m, est un peu arbitraire mais convient bien pour nos latitudes, dans le sens où il permet de beaucoup accélérer les calculs sans que l'erreur due à l'interpolation ne soit visible sur les images finales. De plus, 4096 est une puissance de deux, ce qui permet d'optimiser encore la méthode positionAt en remplaçant une division par un appel à la méthode scalb, passablement plus rapide. Vous êtes libres de mettre en œuvre cette optimisation si vous le désirez — et si vous la comprenez.
2.3 Tests
Comme d'habitude, nous vous fournissons un fichier de vérification de noms contenu dans une archive Zip à importer dans votre projet.
De plus, nous vous conseillons une fois encore de vérifier que vos classes se comportent correctement en générant des images au moyen de petits programmes de déboguage. Nous vous en proposons deux ci-dessous, un pour dessiner le contenu des fichiers HGT, l'autre pour dessiner un profil altimétrique.
2.3.1 Dessin de fichier HGT
Pour vérifier que les données des fichiers HGT sont bien chargées, une technique consiste à générer une image se basant sur les altitudes des points et de voir si elle correspond à la réalité. Une telle image est similaire à celle produite par le programme DrawDEM de l'étape précédente.
Le programme ci-dessous fait exactement cela, en générant une image carrée de 300 pixels de côté représentant une zone d'un demi degré dont le coin sud-ouest a les coordonnées (6.25°, 46.25°) et le coin nord-est les coordonnées (6.75°, 46.75°). L'extrait de carte ci-dessous montre cette zone.
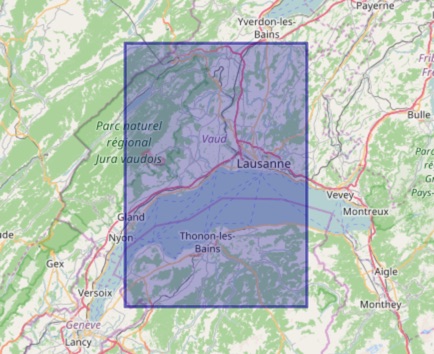
Figure 4 : Zone dessinée par DrawHgtDEM (carte OpenStreetMap)
Notez que la raison pour laquelle cette zone apparaît rectangulaire ici mais carré plus bas est que cette carte utilise la projection de Mercator alors que le programme plus bas utilise une projection dite « plate carrée ».
Pour alléger la présentation du programme, les énoncés d'importation (import) ont été omis mais sont similaires à ceux du programme d'exemple de l'étape précédente. Pour la même raison, la méthode gray, en tout point identique à celle de l'étape précédente, a également été omise.
final class DrawHgtDEM {
final static File HGT_FILE = new File("N46E006.hgt");
final static double ORIGIN_LON = toRadians(6.25);
final static double ORIGIN_LAT = toRadians(46.25);
final static double WIDTH = toRadians(0.5);
final static int IMAGE_SIZE = 300;
final static double MIN_ELEVATION = 200;
final static double MAX_ELEVATION = 1_500;
public static void main(String[] as) throws Exception {
DiscreteElevationModel dDEM =
new HgtDiscreteElevationModel(HGT_FILE);
ContinuousElevationModel cDEM =
new ContinuousElevationModel(dDEM);
double step = WIDTH / (IMAGE_SIZE - 1);
BufferedImage i = new BufferedImage(IMAGE_SIZE,
IMAGE_SIZE,
TYPE_INT_RGB);
for (int x = 0; x < IMAGE_SIZE; ++x) {
double lon = ORIGIN_LON + x * step;
for (int y = 0; y < IMAGE_SIZE; ++y) {
double lat = ORIGIN_LAT + y * step;
GeoPoint p = new GeoPoint(lon, lat);
double el =
(cDEM.elevationAt(p) - MIN_ELEVATION)
/ (MAX_ELEVATION - MIN_ELEVATION);
i.setRGB(x, IMAGE_SIZE - 1 - y, gray(el));
}
}
dDEM.close();
ImageIO.write(i, "png", new File("dem.png"));
}
}
En exécutant ce programme, on obtient l'image ci-dessous, sur laquelle le Léman est bien visible dans la moitié inférieure. On devine aussi le lac de Joux en haut à gauche, et les vallées creusées par les principaux cours d'eau apparaissent clairement.
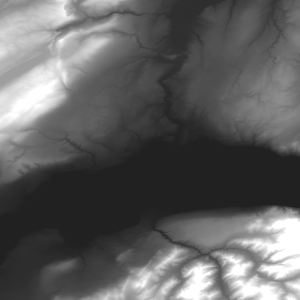
Figure 5 : Relief dans la région lémanique
2.3.2 Dessin de profil altimétrique
Pour vérifier le calcul des profils altimétriques, il est aussi possible de les dessiner.
Le programme ci-dessous dessine le même profil que celui de la figure 3 — qui part des Pierres du Niton et va jusqu'à la gare de la Chaux-de-Fonds — mais en utilisant les données des fichiers HGT fournis. Une fois encore, les énoncés d'importation ont été omis pour alléger la présentation.
final class DrawElevationProfile {
final static File HGT_FILE = new File("N46E006.hgt");
final static double MAX_ELEVATION = 1_500;
final static int LENGTH = 111_000;
final static double AZIMUTH = toRadians(27.97);
final static double LONGITUDE = toRadians(6.15432);
final static double LATITUDE = toRadians(46.20562);
final static int WIDTH = 800, HEIGHT = 100;
public static void main(String[] as) throws Exception {
DiscreteElevationModel dDEM =
new HgtDiscreteElevationModel(HGT_FILE);
ContinuousElevationModel cDEM =
new ContinuousElevationModel(dDEM);
GeoPoint o =
new GeoPoint(LONGITUDE, LATITUDE);
ElevationProfile p =
new ElevationProfile(cDEM, o, AZIMUTH, LENGTH);
int BLACK = 0x00_00_00, WHITE = 0xFF_FF_FF;
BufferedImage i =
new BufferedImage(WIDTH, HEIGHT, TYPE_INT_RGB);
for (int x = 0; x < WIDTH; ++x) {
double pX = x * (double) LENGTH / (WIDTH - 1);
double pY = p.elevationAt(pX);
int yL = (int)((pY / MAX_ELEVATION) * (HEIGHT - 1));
for (int y = 0; y < HEIGHT; ++y) {
int color = y < yL ? BLACK : WHITE;
i.setRGB(x, HEIGHT - 1 - y, color);
}
}
dDEM.close();
ImageIO.write(i, "png", new File("profile.png"));
}
}
En l'exécutant, on obtient l'image ci-dessous, qui a été redimensionnée ici pour des questions de présentation mais est également disponible en taille réelle.

Figure 6 : Profil des Pierres du Niton à La Chaux-de-Fonds
En comparant ce profil avec celui obtenu sur map.geo.admin.ch, présenté à la figure 3 plus haut, on constate que les deux sont généralement assez similaires, avec toutefois deux différences importantes :
- le nôtre s'arrête brusquement à environ 100 km, car le fichier HGT utilisé ne couvre pas la totalité de la zone couverte par le profil,
- leur profil est nettement plus lisse que le nôtre, car :
- leurs MNT sont plus précis que les nôtres, et
- ils appliquent probablement un filtre de lissage pour rendre leur profil plus doux.
Néanmoins, les ressemblances sont assez importantes pour nous donner confiance en notre programme.
3 Résumé
Pour cette étape, vous devez :
- écrire les classes
HgtDiscreteElevationModeletElevationProfileen fonction des indications données plus haut, - tester ces classes,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 17 mars à 16h30, via le système de rendu.
N'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus et aucun retard, aussi insignifiant soit-il, ne sera toléré !