Ensemble de Mandelbrot
Série 10
Introduction
Le but de cette série est de vous familiariser avec la création d'interfaces utilisateur graphiques en complétant un programme d'exploration de l'ensemble de Mandelbrot.
Pour mémoire, l'ensemble de Mandelbrot — déjà décrit à la série 4 — est l'ensemble des points \(c\) du plan complexe tels que la suite complexe définie par :
\begin{align*} z_0 &= 0\\ z_{n+1} &= z_n^2 + c \end{align*}est bornée.
Dans le cas général, il n'est pas possible de déterminer avec certitude les points pour lesquels cette suite est bornée, et une technique approximative est donc utilisée. Elle consiste à calculer les termes de la suite jusqu'à ce que l'un d'eux ait un module supérieur à 2, ou que l'on ait calculé un nombre maximum (et prédéfini) \(M\) de termes, p.ex. 500.
Dans le premier cas, on peut conclure avec certitude que le point ne fait pas partie de l'ensemble de Mandelbrot. Dans le second, on fait l'hypothèse qu'il en fait partie ; cela n'est toutefois pas certain, car le calcul d'un plus grand nombre de termes pourrait révéler qu'il n'en fait en réalité pas partie.
A partir de cette technique de calcul (approximative), on peut obtenir une image intéressante en coloriant chaque point du plan complexe avec une couleur dépendant du nombre d'éléments de la suite de Mandelbrot dont le calcul a été nécessaire pour lui : tous les points faisant partie de l'ensemble sont coloriés en noir, les autres en une teinte de gris reflétant le nombre d'itérations.
En dessinant ainsi une portion du plan complexe située autour de l'origine, on obtient l'image ci-dessous.
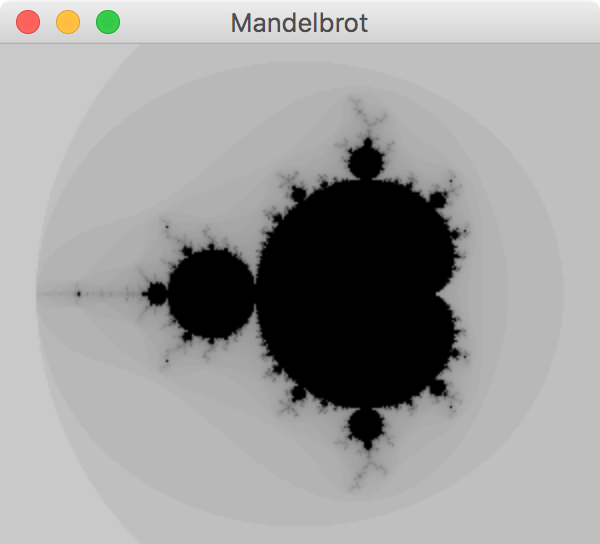
Figure 1 : Image de l'ensemble de Mandelbrot
Pour commencer cette série, créez un nouveau projet Eclipse et importez-y l'archive Zip que nous vous fournissons. Cette archive contient les quatre classes suivantes :
Main, la classe principale construisant l'interface graphique et que vous devrez améliorer,Mandelbrot, une classe représentant un bean JavaFX sachant calculer une image de l'ensemble de Mandelbrot selon la technique décrite plus haut,RectangleetPoint, deux classes immuables représentant respectivement un rectangle et un point.
Avant de continuer, familiarisez-vous rapidement avec ces classes en lisant leur code. Même si vous n'avez pas besoin de comprendre en détail la classe Mandelbrot, il est important que vous sachiez que les propriétés width et height donnent la largeur et la hauteur, en pixels, de l'image, tandis que les propriétés frameCenter et frameWidth donnent respectivement la position du centre et la largeur de la zone du plan dessinée sur l'image. La hauteur de cette zone est déterminée automatiquement afin que l'image finale ne soit pas déformée.
Exercice 1
En lançant l'application fournie, vous devriez voir apparaître une fenêtre similaire à celle de la figure 1. Toutefois, en redimensionnant cette fenêtre, vous devriez constater que l'image, elle, conserve une taille fixe, ce qui est dommage.
Le but de ce premier exercice est de corriger ce problème en faisant en sorte que l'image se redimensionne automatiquement pour toujours occuper la totalité de la fenêtre.
Notez que cela peut se faire très facilement au moyen de liens (bindings) JavaFX et demande un total de 4 lignes de code. Ne cherchez donc pas midi à quatorze heures, et pensez simplement aux différentes propriétés qui devraient être liées pour que le redimensionnement se fasse correctement. En particulier, sachez que les propriétés fitWidth et fitHeight de la classe ImageView font partie de celles à lier.
Exercice 2
Pour permettre l'exploration de l'ensemble de Mandelbrot, ajoutez au programme la possibilité de zoomer en double-cliquant sur l'image.
Pour ce faire, attachez — au moyen de la méthode setOnMouseClicked — un gestionnaire d'événements souris à l'instance de ImageView contenant l'image. Ce gestionnaire commence par vérifier, au moyen de la méthode getClickCount, que l'utilisateur a bien effectué un clic double. Si tel est le cas, elle change la zone du plan dessinée sur l'image de manière à ce que :
- la largeur de la nouvelle zone soient égale à la moitié de celle de l'ancienne zone, ce qui correspond à un facteur de zoom de 2,
- le point P sur lequel le pointeur de la souris se trouvait au moment du clic — dont les coordonnées s'obtiennent au moyen des méthodes
getXetgetY— se retrouve au même endroit à l'écran après le zoom.
Ce comportement correspond, entre autres, à celui des systèmes de cartographie en ligne comme OpenStreetMap ou Google Maps. Une solution raisonnablement simple pour l'obtenir consiste à transformer le rectangle contenant la zone du plan dessinée en trois étapes successives :
- premièrement, le rectangle est translaté afin de placer son coin bas-gauche sur le point P,
- deuxièmement, le rectangle est redimensionné du facteur voulu (ici ½), en conservant la position de son coin bas-gauche,
- troisièmement, le rectangle est à nouveau translaté afin de replacer le point P à sa position initiale.
Les méthodes translatedBy et scaledBy de la classe Rectangle permettent d'effectuer les translations et redimensionnements requis. La principale difficulté ici est de correctement déterminer les paramètres des deux translations. Faites un dessin pour vous faciliter le travail, et ayez bien en tête les deux repères entrant en jeu dans cet exercice : celui du plan, dans lequel le bean de Mandelbrot travaille, et celui du nœud JavaFX contenant l'image. Souvenez-vous que ce dernier a son origine dans le coin haut-gauche de l'image, que son axe des abscisses est dirigé vers la droite et celui des ordonnées vers le bas.
Exercice 3
Améliorez encore le programme en ajoutant les deux fonctionnalités suivantes :
- un double clic effectué lorsque la touche contrôle (ctrl) est enfoncée zoom vers l'arrière plutôt que vers l'avant,
- un clic effectué avec le bouton droit de la souris translate la zone du plan affichée de manière à ce que le point se trouvant sous le pointeur de la souris se retrouve au centre de l'image.
Les méthodes isControlDown et getButton de MouseEvent vous seront utiles pour cela.
Ces ajouts effectués, vérifiez que votre programme se comporte correctement en explorant l'ensemble de Mandelbrot. Vous devriez y découvrir de nombreuses images intéressantes, comme celle ci-dessous.

Figure 2 : Zoom dans l'ensemble de Mandelbrot