Etape 2 – Plateau de jeu
1 Introduction
Le but de cette étape est de définir les classes permettant de représenter le plateau de jeu et son contenu.
1.1 Blocs
Comme cela a été expliqué à l'étape précédente, le plateau de jeu est constitué d'un certain nombre de cases. Chacune de ces cases est occupée par exactement un bloc, p.ex. un mur ou un bonus. Il existe trois sortes de blocs :
- Les blocs libres, sur lesquels les joueurs peuvent se déplacer, des bombes peuvent être posées, et qui n'arrêtent pas les explosions.
- Les murs (au sens large), qui peuvent être soit indestructibles, soit destructibles. Ces derniers s'écroulent lorsqu'ils sont touchés par une explosion et, après s'être écroulés, font place soit à un bloc libre, soit à un bonus.
- Les bonus, sur lesquels les joueurs peuvent se déplacer librement comme sur les blocs libres, mais qui arrêtent les explosions comme les murs. Lorsqu'un joueur atteint la sous-case centrale d'une case contenant un bonus, il consomme celui-ci (qui est remplacé par un bloc libre) et gagne un pouvoir en conséquence.
A chaque type de bloc correspond une image distincte. Dans la version originale de XBlast, de nombreuses images existent pour les différents types de blocs, afin que chaque niveau puisse avoir un style qui lui est propre. Pour ce projet, nous n'utiliserons qu'une seule image par type de bloc. Ces images, extraites de la version originale de XBlast, sont présentées ci-dessous :
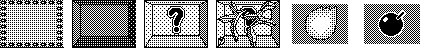
Figure 1 : Représentation graphique des blocs (© Oliver Vogel)
De gauche à droite, elles correspondent à :
- un bloc libre,
- un mur indestructible,
- un mur destructible,
- un mur destructible en train de s'écrouler,
- un bonus augmentant la portée des bombes,
- un bonus augmentant le nombre maximum de bombes.
1.2 Plateau
En première approximation, le plateau n'est rien d'autre qu'un tableau bidimensionnel de blocs, composé de 13 lignes de 15 colonnes chacune. Il est toutefois important de noter que les plateaux typiques de XBlast ne sont pas quelconques, pour deux raisons :
- ils sont généralement murés, c-à-d entourés d'un mur continu indestructible qui arrête les joueurs et explosions,
- ils possèdent généralement un, et plus souvent deux, axes de symétrie.
L'intérêt d'un plateau possédant deux axes de symétrie est qu'il permet de placer initialement chacun des quatre joueurs dans un coin différent du plateau, tout en s'assurant qu'aucun d'entre eux n'est favorisé par son placement.
La figure ci-dessous illustre un plateau muré et symétrique selon deux axes. Sur cette figure, le mur extérieur est représenté en bleu et les cases se trouvant sur l'un des axes de symétrie sont grisées. Les blocs d'un certain nombre de cases centrales sont représentés par les lettres A à I afin de faciliter la compréhension de la symétrie.
Figure 2 : Plateau muré doté de deux axes de symétrie
Comme cette image le montre, un plateau muré et doté de deux axes de symétrie est caractérisé par seulement 42 blocs (6 lignes, 7 colonnes), coloriés ici en rouge. Un exemple d'un tel plateau est celui donné dans l'introduction, comme l'image suivante l'illustre :

Figure 3 : Symétrie et murage du niveau par défaut
Le fait que les plateaux de jeu soient souvent murés et symétriques implique que la création de tels plateaux doit être simple. Par exemple, le plateau ci-dessus devrait pouvoir être créé en ne spécifiant que les 42 blocs rouges.
1.3 Gestion du temps
La gestion du temps est une composante cruciale — et souvent difficile à mettre en œuvre correctement — des jeux d'action.
Pour ce projet, nous adopterons une solution simple, consistant à représenter le temps par un entier, valant 0 en début de partie et progressant unité par unité. La totalité de l'état du jeu (p.ex. la position des joueurs) évolue de manière discrète : l'état au temps \(t + 1\) est calculé en fonction des règles du jeu, de l'état au temps \(t\) et des actions effectuées par les joueurs, p.ex. le dépôt d'une bombe.
Il est très important de comprendre que cette notion de temps est abstraite, et n'a, a priori, pas de lien avec le temps « réel » dans lequel nous vivons. Dès lors, pour éviter toute confusion, nous n'utiliserons plus dans ce qui suit le terme « temps » pour parler de cette notion, mais plutôt les termes de « coup d'horloge » (tick en anglais) ou « pas ».
Tous les aspects temporels du jeu sont ainsi exprimés en un nombre entier de pas. Par exemple, un joueur en mouvement se déplace d'une sous-case par pas ; une explosion se déplace d'une case par pas, donc 16 fois plus vite qu'un joueur ; au début d'une de ses vies, un joueur est invincible durant 64 pas ; et ainsi de suite.
Comme nous le verrons par la suite, l'évolution discrète de l'état facilite beaucoup la programmation. Par exemple, étant donné ce qui précède, il est clair qu'à chaque coup d'horloge, un joueur se trouve sur une et une seule sous-case : il ne lui est pas possible de se retrouver entre deux sous-cases. De même, une case est soit totalement recouverte d'une explosion, soit libre de toute explosion : il n'est pas possible d'avoir une case partiellement couverte d'une explosion. Il en découle que déterminer si un joueur est touché par une explosion est très simple et revient à vérifier si la sous-case qu'il occupe fait partie d'une case actuellement recouverte par une explosion.
Bien entendu, étant donnée qu'une partie de XBlast se déroule en temps réel, il faut, d'une manière ou d'une autre, lier les coups d'horloge au temps réel. Comme nous le verrons dans une étape ultérieure, ce lien est établi par la boucle centrale du serveur, qui fait évoluer l'état 20 fois par secondes. Ainsi, une explosion se déplace à la vitesse de 20 cases par seconde, tandis qu'un joueur se déplace à 1.25 (20/16) cases par seconde.
1.4 Evolution du plateau
Comme cela a été mentionné ci-dessus, le contenu du plateau de jeu peut évoluer. Par exemple, lorsqu'un mur destructible est touché par une explosion, il commence à s'écrouler et, au bout d'un certain nombre de coups d'horloge, fait place à un bonus ou à un bloc libre.
La figure ci-dessous évoque l'évolution temporelle d'un tel mur destructible touché par une explosion et faisant place, après n coups d'horloge, à un bonus. L'état du bloc à chaque coup d'horloge est représenté par son image, et les flèches évoquent l'évolution temporelle.
Figure 4 : Evolution d'un mur atteint par une explosion
Il faut noter que l'illustration ci-dessus fait l'hypothèse que le bloc reste un bonus pour toujours, ou en tout cas jusqu'à la fin de la partie. En pratique, ce n'est pas forcément le cas, car son évolution dépend des interactions avec d'autres éléments du jeu. Par exemple, si le bonus est atteint par une explosion, il disparaît et fait place à un bloc libre au bout d'un certain nombre de coups d'horloge. De même, si un joueur se déplace sur la sous-case centrale de la case contenant le bonus, ce dernier est consommé par le joueur et fait place immédiatement à un bloc libre. Néanmoins, cette illustration suggère une idée intéressante : l'évolution temporelle d'un élément du plateau de jeu peut être représentée par la séquence de ses états futurs.
Ainsi, plutôt que de représenter le plateau par un simple tableau bidimensionnel de blocs, comme proposé plus haut, on peut le représenter par un tableau bidimensionnel de séquences de blocs. Avec une telle représentation, déterminer le prochain état du plateau est trivial : il suffit de prendre le prochain élément de chacune de ces séquences. (On ignore ici, dans un premier temps, l'interaction avec les autres éléments du jeu.)
Cette idée est illustrée dans la figure ci-dessous, qui montre un plateau de 4 cases (2 lignes, 2 colonnes). A chaque case du plateau est associée une séquence de blocs, chaque élément de la séquence correspondant à un coup d'horloge. Par exemple, les blocs grisés et liés entre eux par une flèche constituent la séquence des blocs occupant la case sud-est du plateau. (Les flèches liant les blocs des trois autres séquences ne sont pas représentées pour ne pas alourdir l'image).
Figure 5 : Séquences de blocs d'un plateau simple
La figure ci-dessus ne montre pas de quel type sont les blocs de la séquence grisée, mais on pourrait imaginer que les deux premiers soient un mur en train de s'écrouler, et les deux derniers un bonus.
2 Mise en œuvre Java
Le gros de la mise en œuvre des concepts de cette étape consiste en l'énumération Block représentant un bloc, et la classe Board représentant le plateau. Toutefois, une interface (Ticks) et une classe (Lists) auxiliaires doivent également être écrites.
L'interface Ticks, l'énumération Block et la classe Board ne seront utilisées que par le serveur du jeu : le client, très simple, n'a pas connaissance de ces concepts. Pour cette raison, ces entités sont placées dans le sous-paquetage ch.epfl.xblast.server, réservé au code spécifique au serveur.
2.1 Interface Ticks
L'interface Ticks du paquetage ch.epfl.xblast.server définit la durée, en coups d'horloge, de différents aspects du jeu. Notez qu'il n'est pas très important, à ce stade, de bien comprendre à quoi correspondent ces différentes durées, leur signification deviendra claire lors d'étapes ultérieures.
Les constantes suivantes, publiques, statiques et de type int, sont définies :
PLAYER_DYING_TICKS, la durée de la période durant laquelle un joueur est mourant (8),PLAYER_INVULNERABLE_TICKS, la durée de la période d'invulnérabilité d'un joueur (64),BOMB_FUSE_TICKS, la durée de consommation de la mèche d'une bombe, c-à-d le temps avant qu'elle n'explose (100),EXPLOSION_TICKS, la durée d'explosion d'une bombe (30),WALL_CRUMBLING_TICKS, la durée d'écroulement d'un mur destructible (identique àEXPLOSION_TICKS),BONUS_DISAPPEARING_TICKS, la durée de disparition d'un bonus atteint par une explosion (identique àEXPLOSION_TICKS).
2.2 Enumération Block
L'énumération Block du paquetage ch.epfl.xblast.server, publique, définit les différents types de blocs, à savoir :
FREE, qui représente un bloc libre,INDESTRUCTIBLE_WALL, qui représente un mur indestructible,DESTRUCTIBLE_WALLqui représente un mur destructible,CRUMBLING_WALL, qui représente un mur (destructible) en train de s'écrouler.
Les méthodes publiques suivantes, qui permettent de tester certaines propriétés des blocs, sont définies pour cette énumération :
boolean isFree(), qui retourne vrai si et seulement si le bloc est libre, ce qui n'est vrai que pour le blocFREE,boolean canHostPlayer(), qui retourne vrai si et seulement si le bloc peut héberger un joueur, ce qui pour l'instant n'est le cas que s'il est libre,boolean castsShadow(), qui retourne vrai si et seulement si le bloc projette une ombre sur le plateau de jeu, ce qui n'est vrai que pour les murs (dont le nom se termine par_WALL).
Notez qu'il manque encore deux valeurs à cette énumération, celles représentant les blocs de type bonus. Elles seront ajoutées lors d'une étape ultérieure, une fois que la classe représentant les bonus aura été définie.
2.3 Classe Lists
La classe Lists du paquetage ch.epfl.xblast, publique, finale et non instanciable (c-à-d que son constructeur par défaut est privé et vide), contient des méthodes statiques travaillant sur les listes. Pour cette étape, la seule méthode à définir est la suivante :
<T> List<T> mirrored(List<T> l), qui retourne une version symétrique de la liste donnée, ou lève l'exceptionIllegalArgumentExceptionsi celle-ci est vide.
Par exemple, appliquée à la liste de chaînes ["k", "a", "y"], cette méthode retourne une liste contenant les chaînes ["k", "a", "y", "a", "k"]. Notez que l'élément final de la liste originale (ici la chaîne y) n'apparaît qu'une fois dans le résultat.
L'écriture de cette méthode peut être simplifiée par l'utilisation judicieuse des méthodes suivantes :
subListdeList, qui permet d'obtenir une vue sur une sous-liste de la liste à laquelle on l'applique, etreversedeCollections, qui permet d'inverser l'ordre des éléments de la liste qu'on lui passe.
2.4 Classe Sq
Avant d'examiner la mise en œuvre du plateau de jeu, il convient de décrire comment représenter les séquences de blocs, étant donné que le plateau est un tableau de telle séquences.
En regardant la figure 4, on pourrait assez logiquement penser utiliser une liste de type List<Block> pour stocker les états futurs d'un bloc. Cette idée n'est pas mauvaise, mais les listes Java ont deux inconvénients empêchant leur utilisation ici :
- elles sont finies, et il n'est donc pas possible de les utiliser pour représenter des séquences infinies comme celle de la figure 4,
- elles ne sont pas immuables, ce qui complique passablement leur utilisation.
Comme nous le verrons plus tard dans le cours, Java offre une notion de flot (stream) qui résout le premier de ces problèmes, les flots étant en quelque sorte des listes potentiellement infinies. Malheureusement, les flots Java ne sont pas immuables non plus.
Dès lors, aucune des classes de la bibliothèque Java ne semble idéale pour représenter les séquences d'état. Nous mettons donc à votre disposition la classe générique ch.epfl.cs108.Sq<T> (pour sequence) représentant une séquence, potentiellement infinie, de valeurs de type T. Dès lors, le plateau de jeu sera représenté comme un tableau bidimensionnel de séquences de blocs, c-à-d de valeurs de type Sq<Block>.
La classe Sq vous est fournie sous la forme d'un fichier JAR à télécharger et à ajouter à votre projet en suivant les indications données sur la page consacrée à ce sujet.
L'utilisation de la classe Sq n'est pas totalement triviale, mais nous la découvrirons progressivement au cours des étapes du projet. Pour l'instant, il importe de savoir qu'une séquence peut être consultée au moyen des trois méthodes suivantes :
boolean isEmpty(), qui retourne vrai si et seulement si la séquence est vide,T head(), qui retourne le premier élément (ou tête) de la séquence, ou lève l'exceptionNoSuchElementExceptionsi elle est vide,Sq<T> tail(), qui retourne la queue de la séquence, c-à-d la séquence amputée de son premier élément, ou lève l'exceptionNoSuchElementExceptionsi elle est vide.
Plusieurs méthodes existent pour construire des séquences ou les combiner entre elles, mais la seule nécessaire pour cette étape est la méthode (statique) constant. Elle permet de construire une séquence constante composée d'une valeur répétée à l'infini.
Par exemple, l'extrait de programme suivant affiche blablabla à l'écran, en affichant les trois premiers éléments de la séquence infinie dont tous les éléments sont la chaîne bla :
Sq<String> s = Sq.constant("bla");
for (int i = 0; i < 3; ++i) {
System.out.print(s.head());
s = s.tail();
}
2.5 Classe Board
La classe Board du paquetage ch.epfl.xblast.server, publique, finale et immuable, représente un plateau de jeu.
Comme expliqué ci-dessus, ce plateau est conceptuellement un tableau bidimensionnel de séquences de blocs. En réalité, pour faciliter les choses, ce tableau bidimensionnel est stocké sous la forme d'une liste unidimensionnelle. Les séquences de blocs sont stockées dans cette liste dans l'ordre de lecture (row major) décrit dans l'étape précédente. En d'autres termes, le plateau est représenté par une liste de 195 séquences de blocs. La première de ces séquences correspond à la case nord-ouest, la seconde à sa voisine de l'est, et ainsi de suite jusqu'à la dernière séquence, qui correspond à la case sud-est.
La classe Board comporte donc un unique champ privé de type List<Sq<Block>> dans lequel les séquences de blocs sont stockées. Le premier élément de cette liste, de type Sq<Block>, est la séquence de blocs de la case nord-ouest du plateau ; le premier élément de cette séquence, de type Block, est le bloc à un coup d'horloge donné, le second au coup d'horloge suivant, et ainsi de suite.
Notez qu'à ce stade du développement du jeu, la totalité des séquences de blocs constituant le plateau sont constantes, et elles peuvent donc sembler inutiles ! Leur utilité deviendra apparente plus tard, lors de l'écriture du code gérant l'interaction entre les murs destructibles et les explosions (entre autres).
La classe Board offre un unique constructeur public prenant en argument la totalité des séquences de blocs du plateau, sous la forme de liste :
Board(List<Sq<Block>> blocks), qui construit un plateau avec les séquences de blocs données, ou lève l'exceptionIllegalArgumentExceptionsi la liste passée en argument ne contient pas 195 éléments.
En plus de cet unique constructeur, la classe Board offre plusieurs méthodes permettant de construire facilement des plateaux constants, symétriques et/ou murés. Par plateau constant, on entend un plateau qui associe à chacune des cases une séquence constante (et infinie) d'un seul et même bloc.
Ces méthodes de construction de plateaux constants, statiques et publiques, sont :
Board ofRows(List<List<Block>> rows), qui construit un plateau constant avec la matrice de blocs donnée, ou lève l'exceptionIllegalArgumentExceptionsi la liste reçue n'est pas constituée de 13 listes de 15 éléments chacune,Board ofInnerBlocksWalled(List<List<Block>> innerBlocks), qui construit un plateau muré avec les blocs intérieurs donnés, ou lève l'exceptionIllegalArgumentExceptionsi la liste reçue n'est pas constituée de 11 listes de 13 éléments chacune,Board ofQuadrantNWBlocksWalled(List<List<Block>> quadrantNWBlocks), qui construit un plateau muré symétrique avec les blocs du quadrant nord-ouest donnés, ou lève l'exceptionIllegalArgumentExceptionsi la liste reçue n'est pas constituée de 6 listes de 7 éléments chacune.
A l'aide de ces méthodes, le plateau de jeu de la figure 3, symétrique et muré, pourrait se définir ainsi :
Block __ = Block.FREE;
Block XX = Block.INDESTRUCTIBLE_WALL;
Block xx = Block.DESTRUCTIBLE_WALL;
Board board = Board.ofQuadrantNWBlocksWalled(
Arrays.asList(
Arrays.asList(__, __, __, __, __, xx, __),
Arrays.asList(__, XX, xx, XX, xx, XX, xx),
Arrays.asList(__, xx, __, __, __, xx, __),
Arrays.asList(xx, XX, __, XX, XX, XX, XX),
Arrays.asList(__, xx, __, xx, __, __, __),
Arrays.asList(xx, XX, xx, XX, xx, XX, __)));
En comparant cet extrait de programme avec la partie rouge de la figure 3, on constate que grâce à la méthode ofQuadrantNWBlocksWalled et aux variables de deux lettres définies pour les différents types de blocs (__, xx et XX), la correspondance entre le code créant le plateau et la représentation graphique de ce dernier est assez évidente.
La classe Board offre également les deux méthodes publiques suivantes, qui donnent accès à son contenu :
Sq<Block> blocksAt(Cell c), qui retourne la séquence des blocs pour la case donnée,Block blockAt(Cell c), qui retourne le bloc pour la case donnée, c-à-d la tête de la séquence retournée par la méthode précédente.
Notez que les noms de ces deux méthodes ne diffère que par le fait que le premier est un pluriel, car la méthode retourne une séquence de blocs, tandis que le second est un singulier, car la méthode retourne un bloc. De telles paires de méthodes nommées de manière similaire se retrouveront dans d'autres classes.
2.5.1 Validation des matrices de blocs
Plusieurs méthodes de Board doivent valider les matrices (listes de listes) de blocs reçues en argument et lever l'exception IllegalArgumentException si elles n'ont pas la bonne forme. Pour faciliter cette vérification, nous vous conseillons d'ajouter la méthode statique et privée suivante à la classe :
void checkBlockMatrix(List<List<Block>> matrix, int rows, int columns), qui lève l'exceptionIllegalArgumentExceptionsi la matrice (liste de liste) donnée ne contient pasrowséléments, contenant chacuncolumnsblocs.
Notez que si cette méthode était utile dans d'autres parties du programme, elle pourrait être rendue générique et placées dans une classe séparée. Comme ce n'est pas le cas, elle est laissée dans la classe Board, dans un soucis de simplicité.
2.5.2 Construction des plateaux symétriques et murés
L'écriture des méthodes de construction des plateaux symétriques et murés peut être considérablement facilitée par l'utilisation judicieuse des méthodes suivantes :
- la méthode
mirroredde la classeLists(écrite précédemment), - la méthode
nCopiesde la classeCollections.
2.6 Tests
A partir de cette étape, nous ne vous fournissons plus de tests unitaires. Il vous faut donc les écrire vous-même si vous désirez en avoir, ce qui est fortement conseillé.
Nous vous fournissons néanmoins une archive Zip à importer dans votre projet, qui contient le fichier de vérification de noms correspondant à cette étape.
3 Résumé
Pour cette étape, vous devez :
- écrire l'interface
Ticks, l'énumérationBlocket les classesListsetBoarden fonction des spécifications données plus haut, - tester votre code,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre code au plus tard le 4 mars 2016 à 17h30, via le système de rendu, afin d'obtenir les 3 points associés à ce rendu mineur.
Attention : n'attendez surtout pas le dernier moment pour effectuer votre rendu, car vous n'êtes pas à l'abri d'imprévus et aucun retard, aussi insignifiant soit-il, ne sera toléré !
Notez que votre code n'a pas besoin de fonctionner ou d'être documenté pour être accepté par le système de rendu. La seule chose qui compte est que les classes et méthodes publiques de cette étape existent afin qu'aucune erreur n'apparaissent dans les fichiers de vérification de noms. Dès ce moment, vous pouvez rendre votre code et collecter les points du rendu mineur, ce que nous vous conseillons fortement de faire dès que possible. Rien ne vous empêche d'effectuer ensuite d'autre rendus pour la même étape au fur et à mesure de votre progression.