Etape 11 – Relief ombré
1 Introduction
Le but de cette dernière étape du projet est double : premièrement, écrire le code permettant de dessiner un relief ombré et de le combiner aux images de carte pour obtenir le résultat final ; deuxièmement, écrire un programme principal permettant de dessiner facilement des cartes au 1:25'000, à une résolution choisie. Ce programme principal constitue le résultat final du projet.
1.1 Relief ombré
Un relief ombré (shaded relief) est une représentation bidimensionnelle de la topographie d'une zone de la Terre.
De nombreuses techniques existent pour dessiner automatiquement un relief ombré à partir d'un modèle du terrain. Celle que nous utiliserons consiste à choisir la position d'une source lumineuse puis à dessiner en teintes claires les parties du relief y faisant face, en teintes foncées celles n'y faisant pas face.
La plupart des reliefs ombrés utilisés en cartographie sont réalisés avec une source lumineuse provenant du coin haut-gauche de la carte, c-à-d du nord-ouest. Cette source lumineuse est supposée assez éloignée pour que les rayons qu'elle projette soient tous parallèles. Dès lors, elle peut être simplement caractérisée par un vecteur \(\vec{l}\) pointant dans sa direction. Par exemple, le vecteur
\begin{displaymath} \vec{l} = \begin{pmatrix} -1\\ 1\\ 1 \end{pmatrix} \end{displaymath}correspond à une source lumineuse provenant du nord-ouest et faisant un angle d'environ 35° avec l'horizon.
Une fois le vecteur pointant vers la source lumineuse choisi, il reste à savoir comment déterminer la teinte de chaque point du relief ombré. Une idée assez naturelle consiste à utiliser le cosinus de l'angle entre le vecteur pointant vers la source lumineuse et le vecteur normal au relief en ce point pour déterminer sa teinte. En effet, lorsque cet angle est nul, le relief fait directement face à la source lumineuse, et est donc éclairé au maximum. A l'inverse, lorsque cet angle vaut 180°, le relief « tourne le dos » à la lumière et n'est donc pas illuminé du tout.
Dès lors, le niveau de gris \(g\) — compris entre 0 et 1, 0 représentant le noir, 1 le blanc — d'un point du relief ombré où le vecteur normal au terrain est \(\vec{n}\) peut s'obtenir au moyen de la formule suivante :
\begin{displaymath} g = \tfrac{1}{2}(\cos\theta + 1) \end{displaymath}où \(\theta\) est l'angle entre \(\vec{n}\) et \(\vec{l}\). Une manière simple de déterminer le cosinus de cet angle consiste à utiliser le produit scalaire, sachant qu'il possède la propriété suivante :
\begin{displaymath} \vec{u}\cdot\vec{v} = \|\vec{u}\|\,\|\vec{v}\|\cos\theta \end{displaymath}où \(\theta\) est l'angle entre les vecteurs \(\vec{u}\) et \(\vec{v}\).
L'animation ci-dessous montre l'effet du vecteur lumière utilisé sur le relief obtenu. Le vecteur utilisé ici est horizontal et sa direction est indiquée visuellement dans le coin bas-droite de l'image.

Figure 1 : Le Simmental et ses environs, éclairé sous différents angles
Un relief ombré ne doit pas forcément être dessiné en nuances de gris. Une idée intéressante, qu'Eduard Imhof utilisait souvent sur ses cartes, consiste à rendre les pentes exposées légèrement jaunes et les pentes à l'ombre légèrement bleues. Un tel ombrage a un aspect naturel, les pentes exposées au soleil étant effectivement jaunâtres dans la nature, et les pentes à l'ombre bleuâtres, comme le savent les photographes.
Un relief ombré coloré de la sorte est simple à obtenir lorsque les couleurs sont composées d'un mélange de rouge, vert et bleu. En effet, il suffit de faire en sorte que les pentes exposées aient un peu moins de bleu que de rouge et de vert, et les pentes à l'ombre un peu plus. Cet effet s'obtient facilement en réduisant l'amplitude des oscillation de la composante bleue, par exemple au moyen des formules suivantes :
\begin{align} r &= \tfrac{1}{2}\left(\cos\theta + 1\right)\\ g &= \tfrac{1}{2}\left(\cos\theta + 1\right)\\ b &= \tfrac{1}{2}\left(0.7\cos\theta + 1\right) \end{align}Avec ces formules, la couleur d'une pente faisant face à la source lumineuse, donc pour laquelle \(\cos\theta = 1\), est un jaune clair \((1, 1, 0.85)\) tandis que la couleur d'une pente lui tournant le dos, donc pour laquelle \(\cos\theta = -1\), est un bleu foncé \((0,0,0.15)\).
La figure ci-dessous montre l'image obtenue pour le même relief, d'abord en nuances de gris, ensuite en couleurs, en utilisant les formules ci-dessus.

Figure 2 : Le Simmental et ses environs, en nuances de gris et en couleur
1.2 Floutage
En raison de la résolution relativement peu élevée des MNT à notre disposition et de la technique simpliste de calcul du vecteur normal utilisée, les reliefs ombrés obtenus par l'approche décrite ci-dessus produisent un résultat peu plaisant si on les ajoute tels quels à une carte au 1:25'000. Ce défaut ne se voit pas sur les images ci-dessus, à bien plus large échelle, mais est évident dans la figure ci-dessous montrant un extrait de la carte d'Interlaken à laquelle le relief brut a été ajouté.
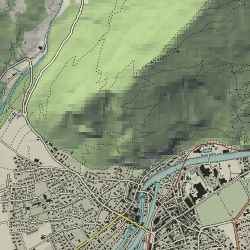
Figure 3 : Le nord d'Interlaken avec un relief brut
Une manière de résoudre ce problème consiste à flouter légèrement les images des reliefs ombrés avant de les combiner avec les images des cartes1. En utilisant cette technique sur la carte d'Interlaken ci-dessus, on obtient le résultat illustré ci-dessous, bien plus plaisant.
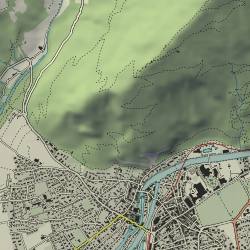
Figure 4 : Le nord d'Interlaken avec un relief adouci par floutage
La version floutée d'une image discrète s'obtient simplement en calculant, pour chaque pixel, une moyenne pondérée de sa couleur à lui et de celle d'un certain nombre de ses voisins.
Par exemple, on peut obtenir une version très légèrement floutée d'une image en calculant, pour chaque pixel de l'image originale, une moyenne pondérée de ses quatre voisins immédiats (avec un poids de 0.1) et du pixel lui-même (avec un poids de 0.6). Une telle transformation peut s'exprimer par une formule donnant la couleur \(p'_{i,j}\) du pixel d'indice \((i,j)\) de l'image transformée en fonction de la couleur \(p\) d'un certain nombre de pixels de l'image originale :
\begin{displaymath} p'_{i, j} = 0.1\,p_{i, j-1} + 0.1\,p_{i-1, j} + 0.6\,p_{i, j} + 0.1\,p_{i+1, j} + 0.1\,p_{i,j+1} \end{displaymath}Etant donné que seuls les poids varient dans cette formule, une transformation de ce genre est souvent spécifiée par une matrice les contenant, nommée noyau (kernel). Ainsi, le noyau correspondant à la formule ci-dessus est :
\begin{pmatrix} 0 & 0.1 & 0\\ 0.1 & 0.6 & 0.1\\ 0 & 0.1 & 0 \end{pmatrix}Ce noyeau est normalisé, c'est-à-dire que la somme de ses poids vaut 1. Cette propriété est importante car elle garantit que la luminosité de l'image n'est pas affectée par la transformation.
Les poids d'un noyau de floutage peuvent être obtenus par échantillonnage d'une fonction gaussienne à deux dimensions, centrée sur l'élément central du noyau, ce qui donne de bons résultats en pratique. Le floutage qui en résulte est généralement appelé flou gaussien (gaussian blur).
Pour mémoire, une fonction gaussienne à deux dimensions, symétrique et centrée à l'origine a la forme suivante :
\begin{displaymath} f(x, y) = e^{\frac{-(x^2 + y^2)}{2\sigma^2}} \end{displaymath}où \(\sigma\) est un paramètre contrôlant le diamètre du monticule illustré dans le graphe de la fonction ci-dessous : plus \(\sigma\) est grand et plus ce monticule est étendu.
Figure 5 : Gaussienne 2D avec \(\sigma = 1\) (source : Wikimedia commons)
Un problème de la fonction gaussienne est qu'elle n'est jamais nulle. En théorie, il faudrait donc utiliser un noyau de taille infinie pour effectuer un flou gaussien. En pratique, étant donné que la fonction gaussienne s'approche très vite de zéro lorsqu'on s'éloigne de son centre, il est possible de considérer comme nuls tous les poids situés au-delà d'une distance limite, souvent choisie comme valant \(3\sigma\).
Dès lors, plutôt que de paramétrer un flou gaussien directement en donnant la valeur de \(\sigma\), il est plus simple de le faire en spécifiant ce que l'on nomme son rayon \(r\), un nombre réel exprimé en pixels. Ce rayon est utilisé d'une part pour déterminer la valeur de \(\sigma\) et d'autre part pour déterminer la taille du noyau \(n\times n\), de la manière suivante :
\begin{align} \sigma &= \frac{r}{3}\\ n &= 2\lceil r\rceil + 1 \end{align}où \(\lceil x\rceil\) représente la partie entière par excès de \(x\) (fonction ceil en anglais), c-à-d le plus petit entier supérieur ou égal à \(x\).
Par exemple, si \(r\) vaut 0.9 alors \(\sigma\) vaut 0.3 et \(n\) vaut 3. Le noyau \(K\) est donc la matrice \(3\times 3\) suivante (les poids ont été arrondis à 6 décimales) :
\begin{pmatrix} 0.000015 & 0.003866 & 0.000015\\ 0.003866 & 1.000000 & 0.003866\\ 0.000015 & 0.003866 & 0.000015 \end{pmatrix}Par exemple, le poids d'indice (1, 2), noté \(K_{1,2}\) se calcule ainsi :
\begin{align} K_{1,2} &= e^{\frac{-(0^2 + (-1)^2)}{2\cdot 0.3^2}}\\ &= e^{\frac{-1}{0.18}}\\ &≈ 0.003866 \end{align}Avant d'être utilisé, ce noyau devrait encore être normalisé en divisant chacun de ses poids par leur somme. Cela n'a pas été fait ici pour simplifier la compréhension.
Le défaut des noyaux obtenus par la technique mentionnée à l'instant est qu'ils sont gros et nécessitent dès lors beaucoup de calculs. En effet, le floutage d'une image avec un noyau de taille \(n\times n\) demande le calcul de \(n^2\) valeurs par pixel.
Il est possible de diminuer ce nombre de calculs en tirant parti du fait que le flou gaussien est ce que l'on appelle séparable. Cela signifie qu'un floutage gaussien bidimensionnel est équivalent à un enchaînement de deux floutages gaussiens unidimensionnels, l'un horizontal, l'autre vertical. Chacun de ces deux floutages unidimensionnels nécessitant le calcul de \(n\) valeurs par pixels, un total de seulement \(2n\) valeurs doivent être calculées par pixels avec cette technique alternative, ce qui constitue un gain appréciable.
La figure ci-dessous illustre le floutage gaussien d'un relief par un enchaînement d'un floutage horizontal et d'un floutage vertical.

Figure 6 : Un relief brut, flouté horizontalement puis verticalement
Le noyau du filtre horizontal est une matrice ligne de taille \(n\) et le noyau du filtre vertical est sa transposée, donc une matrice colonne de taille \(n\). Les coefficients de ces noyaux se calculent au moyen de la fonction gaussienne à une dimension :
\begin{displaymath} f(x) = e^{-\frac{x^2}{2\sigma^2}} \end{displaymath}où \(\sigma\) est la même valeur que celle utilisée dans le cas bidimensionnel. Dès lors, le noyau unidimensionnel horizontal est simplement la ligne centrale du noyau bidimensionnel, tandis que le noyau unidimensionnel vertical est sa colonne centrale.
Par exemple, pour le cas du filtre gaussien de rayon \(r = 0.9\), le noyau du filtre horizontal, avant normalisation, est :
\begin{pmatrix} 0.003866 & 1.000000 & 0.003866 \end{pmatrix}Sa version normalisée, \(K_h\), s'obtient en divisant chaque poids par leur somme, et vaut donc approximativement :
\begin{displaymath} K_h = \begin{pmatrix} 0.003836 & 0.992327 & 0.003836 \end{pmatrix} \end{displaymath}et le noyau vertical normalisé, \(K_v\), est simplement sa transposée \(K_h^T\).
Sachant maintenant comment déterminer les noyaux de floutage, un problème reste encore à résoudre, celui des bords de l'image. En effet, pour calculer la valeur d'un pixel de l'image floutée au moyen d'un noyau de taille \(n\), il faut connaître la valeur de ses \(\left\lfloor\tfrac{n}{2}\right\rfloor\) voisins dans chaque direction. Or, pour tous les pixels se trouvant à moins de cette distance d'un bord, certaines de ces valeurs ne sont pas connues.
Ce problème a une solution simple dans notre cas : pour dessiner un relief flouté, on commence par dessiner un relief plus grand incluant une zone tampon dans chaque bord, dimensionnée en fonction du noyau. On floute ensuite cette image puis on en extrait la zone centrale, qui constitue le relief flouté.
Cette idée est illustrée par la figure ci-dessous, qui montre comment obtenir le relief flouté à droite en produisant d'abord un relief plus grand incluant une zone tampon — à l'extérieur du carré orange — adaptée au noyau utilisé — représenté par le carré bleu — puis en floutant ce relief pour obtenir l'image du milieu et finalement en extraire la zone centrale. Comme on le voit, les pixels de la zone tampon ne sont pas affectés par le floutage, car une partie de leurs voisins est inconnue.

Figure 7 : Utilisation d'une zone tampon lors du floutage
1.3 Combinaison
Une fois les images de la carte et du relief (flouté) obtenues, il reste à les combiner entre elles. Cela se fait par multiplication, c'est-à-dire que la couleur de chaque pixel de l'image finale est obtenu par multiplication des couleurs des pixels correspondants dans l'image de la carte et dans celle du relief.
Pour mémoire, la multiplication de deux couleurs, décrite à l'étape 7, se fait par multiplications des composantes deux à deux.
2 Mise en œuvre Java
2.1 Relief ombré
Ecrivez une classe, nommée p.ex. ReliefShader et placée dans le paquetage dédié aux modèles du terrain, permettant de dessiner un relief ombré coloré, selon la technique décrite plus haut.
Le constructeur de cette classe prend en arguments la projection à utiliser, le modèle numérique du terrain et le vecteur pointant dans la direction de la source lumineuse.
L'unique méthode publique de cette classe, nommée p.ex. shadedRelief, prend en arguments :
- les coins bas-gauche et haut-droite du relief à dessiner, en coordonnées du plan,
- la largeur et la hauteur en pixels de l'image à dessiner,
- le rayon de floutage.
Il est conseillé d'organiser cette classe au moyen des méthodes privées suivantes :
- une première permettant de dessiner un relief ombré brut (sans floutage) étant donnés sa taille en pixels et une fonction permettant de passer du repère de l'image à celui du plan,
- une seconde permettant de calculer le noyau du flou gaussien (unidimensionnel) étant donné son rayon,
- une dernière permettant de flouter une image avec un noyau donné.
Lorsque le rayon de floutage vaut zéro, seule la première de ces méthodes est utilisée. Sinon, les poids gaussiens sont d'abord calculés au moyen de la seconde méthode, ce qui permet de déterminer la largeur de la zone tampon nécessaire ; ensuite, l'image d'un relief ombré incluant la zone tampon est dessiné au moyen de la première méthode ; finalement, le relief ombré est flouté au moyen de la troisième méthode puis la région centrale (sans la zone tampon) est extraite au moyen de la méthode getSubimage et retournée.
Pour effectuer le floutage lui-même, le plus simple est d'utiliser les classes de Java2D. La classe Kernel représente un noyau, tandis que la classe ConvolveOp stocke un tel noyau et des paramètres relatifs à son application. Le plus important est celui déterminant comment calculer les valeurs des pixels situés dans la bordure de l'image destination. La valeur EDGE_NO_OP convient ici étant donné la présence de la zone tampon. Une fois une instance de ConvolveOp obtenue, il est possible d'appliquer la transformation qu'elle représente à une image au moyen de sa méthode filter. Notez qu'en passant null comme second argument à cette méthode elle se charge elle-même d'allouer l'image résultat, ce qui est appréciable.
2.2 Programme principal
La version finale du projet ne fournit aucune interface graphique. Au lieu de cela, les paramètres de la carte à dessiner sont passés directement au programme principal. Comme toujours en Java, celui-ci prend la forme d'une classe possédant une méthode statique nommée main, prenant les arguments sous la forme d'un tableau de chaînes de caractères et ne retournant rien. Cette classe doit impérativement se nommer Main et se trouver dans le paquetage ch.epfl.imhof.
Le programme principal doit accepter les huit arguments ci-dessous, dans l'ordre donné :
- le nom (chemin) d'un fichier OSM compressé avec gzip contenant les données de la carte à dessiner,
- le nom (chemin) d'un fichier HGT couvrant la totalité de la zone de la carte à dessiner, zone tampon incluse,
- la longitude du point bas-gauche de la carte, en degrés,
- la latitude du point bas-gauche de la carte, en degrés,
- la longitude du point haut-droite de la carte, en degrés,
- la latitude du point haut-droite de la carte, en degrés,
- la résolution de l'image à dessiner, en points par pouce (dpi),
- le nom (chemin) du fichier PNG à générer.
Les points bas-gauche et haut-droite sont spécifiés dans le système WGS 84, et la projection utilisée est toujours la projection suisse CH 1903. La résolution doit être un nombre entier.
La largeur \(w\) et la hauteur \(h\) de l'image en pixels sont déterminées au moyen des formules suivantes, qui garantissent que les images de cartes produites sont à une échelle de 1:25'000 :
\begin{align} h &= r \frac{1}{25\,000} (\phi_{TR} - \phi_{BL})R\\[0.5em] w &= \frac{x_{TR} - x_{BL}}{y_{TR} - y_{BL}}h \end{align}où \(r\) est la résolution de l'image, en pixels par mètres (!), \(\phi_{TR}\) et \(\phi_{BL}\) sont la latitude en radians du point haut-droite et bas-gauche, respectivement, \(x_{TR}\), \(y_{TR}\), \(x_{BL}\) et \(y_{BL}\) sont les coordonnées projetées de ces points et \(R\) est le rayon de la Terre en mètres — sa valeur est la même que celle utilisée dans l'étape 10.
Les valeurs réeles de \(w\) et \(h\) obtenues doivent être arrondies à l'entier le plus proche, via la méthode round de la classe Math.
Le rayon de floutage est constant et vaut 1.7 mm sur l'image finale. C'est au programme principal de déterminer la taille en pixels correspondante et de la passer à la méthode de dessin de relief.
Pour simplifier les choses, votre programme principal n'a pas besoin de faire de validation des arguments, et peut échouer avec une exception quelconque si l'un des arguments n'est pas valide, ou s'il n'y a pas assez d'arguments.
2.3 Tests
Pour vous permettre de tester votre programme, nous vous fournissons une archive Zip contenant un ensemble d'images correspondant à trois cartes dessinées avec le corrigé du projet. Pour chacune des cartes, trois images vous sont fournies : l'image finale, celle de la carte (sans relief) et celle du relief après floutage.
La première représente Lausanne et sa région et a été obtenue en passant les paramètres suivants au programme principal :
lausanne.osm.gz N46E006.hgt 6.5594 46.5032 6.6508 46.5459 300 lausanne.png
La seconde image représente Interlaken et sa région et a été obtenue en passant les paramètres suivants au programme principal :
interlaken.osm.gz N46E007.hgt 7.8122 46.6645 7.9049 46.7061 300 interlaken.png
La troisième et dernière image représente Berne et sa région et a été obtenue en passant les paramètres suivants au programme principal :
berne.osm.gz N46E007.hgt 7.3912 46.9322 7.4841 46.9742 300 berne.png
3 Résumé
Pour cette étape, vous devez :
- écrire la classe de dessin de relief ombré et celle du programme principal, selon les spécifications données ci-dessus,
- documenter la totalité des entités publiques que vous avez définies,
- rendre votre projet terminé selon les modalités décrites sur la page consacrée au rendu final.
Faites bien attention à ce que la classe de votre programme principal ait le bon nom, à savoir ch.epfl.imhof.Main, et qu'elle accepte les arguments décrits plus haut, dans l'ordre donné. Soyez bien conscients que la moindre erreur à ce niveau rendra impossible le dessin des cartes lors de l'évaluation automatique de votre projet et entraînera la perte de la totalité des points qui y sont attribués.
Notes de bas de page
Une autre solution, peut-être meilleure, aurait été d'utiliser une technique d'interpolation pour faire varier petit à petit le vecteur normal entre deux points du MNT.