Etape 9 – Dessin du réseau routier
1 Introduction
Le but principal de cette étape est d'écrire une classe permettant de générer un peintre pour le réseau routier, dont le dessin n'est pas des plus facile. Son but secondaire est de préparer la suite en écrivant une classe représentant les vecteurs tridimensionnels.
A la fin de cette étape, vous devriez être capables de dessiner des cartes presque complètes, auxquelles seul l'ombrage du relief manque encore ; il leur sera ajouté lors des deux dernières étapes.
1.1 Dessin des routes
Le dessin des routes n'est pas une tâche aisée, pour plusieurs raisons.
Premièrement, il existe plusieurs types de routes — autoroutes, routes principales, secondaires, etc. — et chacun d'entre-eux doit être dessiné de manière légèrement différente.
Deuxièmement, les ponts et tunnels d'un type de route donné doivent être dessinés différemment des autres parties.
Troisièmement, une route ne doit pas être dessinée avec un trait simple, mais avec une bordure (casing en anglais), généralement noire, et un intérieur d'une autre couleur. Ce dessin s'obtient simplement par superposition d'un trait pour l'intérieur, superposé à un trait plus large pour la bordure, comme l'illustre la figure ci-dessous.
Figure 1 : Dessin d'une route par superposition de traits
Pour ces trois raisons, le nombre de peintres de polylignes à combiner pour dessiner un réseau routier devient vite important. Par exemple, le style utilisé pour ce projet distingue 9 types de routes, chacun d'entre-eux nécessitant 5 peintres de polylignes différents, soit un total de 45 peintres.
Il existe toutefois une grande similarité entre ces peintres, qu'il paraît raisonnable d'exploiter en générant autant que possible ces peintres à partir d'un petit nombre de paramètres, et c'est ce que nous ferons ici.
1.2 Peintre de route
Pour un type de route donné, nous utiliserons un total de cinq peintres de polylignes :
- un peintre pour l'intérieur des ponts,
- un peintre pour la bordure des ponts,
- un peintre pour l'intérieur des routes « normales » (ni pont ni tunnel),
- un peintre pour la bordure des routes normales,
- un peintre pour les tunnels, qui n'ont pas de bordure.
Le style de ligne de chacun de ces peintres est obtenu à partir de quatre paramètres seulement — la largeur \(w_i\) et la couleur \(c_i\) du trait de l'intérieur, et la largeur \(w_c\) et la couleur \(c_c\) du trait de la bordure — de la manière suivante :
- l'intérieur des ponts a la largeur \(w_i\), la couleur \(c_i\), la terminaison round, la jointure round et le trait plein,
- la bordure des ponts a la largeur \(w_i + 2w_c\), la couleur \(c_c\), la terminaison butt, la jointure round et le trait plein,
- l'intérieur des routes normales a le même style que l'intérieur des ponts,
- la bordure des routes normales a le même style que la bordure des ponts, sauf la terminaison qui est round,
- les tunnels ont la largeur \(w_i / 2\), la couleur \(c_c\), la terminaison butt, la jointure round et une séquence d'alternance des sections opaques et transparentes de \([2\,w_i, 2\,w_i]\).
Pour différencier les ponts, tunnels et parties « normales » d'une route, il faut savoir que, dans le modèle OSM, un chemin représentant une route et possédant l'attribut bridge (peu importe sa valeur) est un pont, tandis qu'un chemin représentant une route et possédant l'attribut tunnel (peu importe sa valeur) est un tunnel.
1.3 Peintre de réseau routier
Pour obtenir le peintre composite pour un réseau routier comportant plusieurs types de routes, il faut encore savoir comment empiler les différents peintres susmentionnés correspondant à chaque type de route.
On pourrait imaginer qu'il suffit d'empiler dans un premier temps tous les peintres pour chaque type de routes, puis d'empiler ces peintres composites. Malheureusement, le peintre résultant d'une telle composition produit un dessin peu plaisant pour les jonctions entre différents types de route — p.ex. une sortie d'autoroute sur une route principale — puisque la bordure correspondant à l'un des types est visible en travers de la route. Ce problème est illustré à la figure ci-dessous pour le rond-point de la Maladière et ses environs. La version de gauche a été dessinée par un peintre composé de manière incorrecte, selon la technique décrite à l'instant.
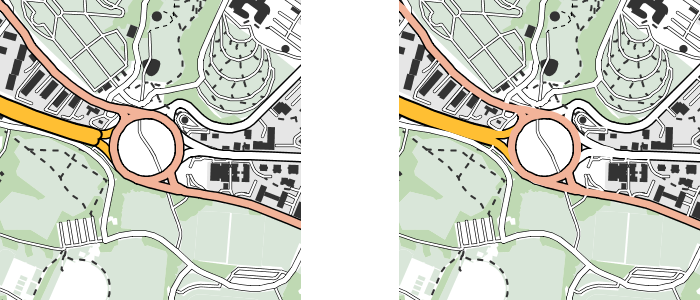
Figure 2 : La Maladière dessinée par un mauvais puis un bon peintre
Dès lors, pour obtenir le peintre composite du réseau routier, il faut générer, pour chaque type de route, les cinq peintres mentionnés plus haut avant de les empiler ainsi (de haut en bas) :
- tous les peintres d'intérieur de ponts,
- tous les peintres de bordure de ponts,
- tous les peintres d'intérieur de routes normales,
- tous les peintres de bordure de routes normales,
- tous les peintres de tunnels.
En procédant de la sorte, on obtient un peintre de réseau routier composite (presque) parfait, qui produit l'image de droite de la figure ci-dessus pour le rond-point de la Maladière.
2 Mise en œuvre Java
2.1 Générateur de peintre de réseau routier
Le générateur de peintre de réseau routier est défini sous la forme d'une classe non instanciable nommée p.ex. RoadPainterGenerator et placée dans le paquetage dédié au dessin.
Sa seule méthode publique — et bien entendu statique — nommée p.ex. painterForRoads, prend un nombre variable de spécifications de routes (concept décrit ci-après) en arguments. Elle retourne le peintre pour le réseau routier correspondant, obtenu selon la technique décrite plus haut. Notez que les peintres de chacun des cinq types donnés doivent être empilés de manière à ce que celui correspondant à la première spécification de route soit au sommet, celui correspondant à la seconde juste en dessous, et ainsi de suite.
Une spécification de route décrit le dessin d'un type de route donné. Elle est composée d'une part d'un filtre (de type Predicate<Attributed<?>>) permettant de sélectionner ce type de route, et d'autre part des quatre paramètres de style (\(w_i\), \(c_i\), \(w_c\) et \(c_c\)) à partir desquels tous les styles des peintres sont déterminés.
2.2 Peintre Suisse
Pour vous permettre de dessiner des cartes ayant le même style que les nôtres — style fortement inspiré des cartes topographiques suisses — nous vous fournissons la définition de notre peintre. Pour faciliter les choses, celui-ci vous est donné directement sous la forme d'un fichier Java, SwissPainter.java, contenant une unique classe créant le peintre et le retournant par le biais d'une méthode statique nommée painter.
Si vous avez nommé vos classes et méthodes en suivant nos suggestions dans les étapes précédentes, vous devriez pouvoir utiliser ce fichier presque tel quel dans votre projet. Si ce n'est pas le cas, n'hésitez pas à le modifier si vous ne voulez pas modifier votre code. Notez néanmoins qu'il est capital que vous ne changiez pas son comportement, car vous devez pouvoir obtenir les mêmes cartes que les nôtres à la fin du projet, une partie de l'évaluation étant basée sur ce point.
2.3 Vecteur tridimensionnel
Le dessin du relief, qui sera le sujet des dernières étapes, nécessite la manipulation de vecteurs tridimensionnels. Votre dernière tâche pour cette étape est donc d'écrire une classe immuable, nommée p.ex. Vector3 et placée dans le paquetage ch.epfl.imhof, représentant un vecteur tridimensionnel. En plus d'un constructeur permettant de créer un vecteur étant données ses trois composantes, cette classe doit offrir les méthodes publiques suivantes :
- une méthode, nommée p.ex.
norm, permettant d'obtenir la norme du vecteur, - une méthode, nommée p.ex.
normalized, permettant d'obtenir la version normalisée du vecteur (c-à-d un vecteur parallèle à celui-ci, de même direction mais de longueur unitaire), - une méthode, nommée p.ex.
scalarProduct, retournant le produit scalaire entre le récepteur et un second vecteur passé en argument.
Pour mémoire, la norme d'un vecteur tridimensionnel est donnée par :
\begin{displaymath} \left\| \begin{pmatrix} x\\ y\\ z \end{pmatrix} \right\| = \sqrt{x^2+y^2+z^2} \end{displaymath}tandis que le produit scalaire entre deux vecteurs tridimensionnels est donné par :
\begin{displaymath} \begin{pmatrix} x_1\\ y_1\\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2\\ y_2\\ z_2 \end{pmatrix} = x_1x_2 + y_1y_2 + z_1z_2 \end{displaymath}2.4 Tests
Pour vous permettre de tester votre projet, nous vous fournissons deux images de cartes obtenues au moyen du peintre suisse donné plus haut.
La première est une carte de Lausanne et sa région, de 1600 par 1060 pixels, à une résolution de 150 dpi, présentée ci-dessous. Dans le système CH1903, les coordonnées du point bas-gauche sont (532510, 150590) et celles du coin haut-droite (539570, 155260).
Comme précédemment, cette image étant redimensionnée par votre navigateur, il vous faut télécharger la version originale sur votre ordinateur pour effectuer une comparaison avec l'image que vous obtenez.
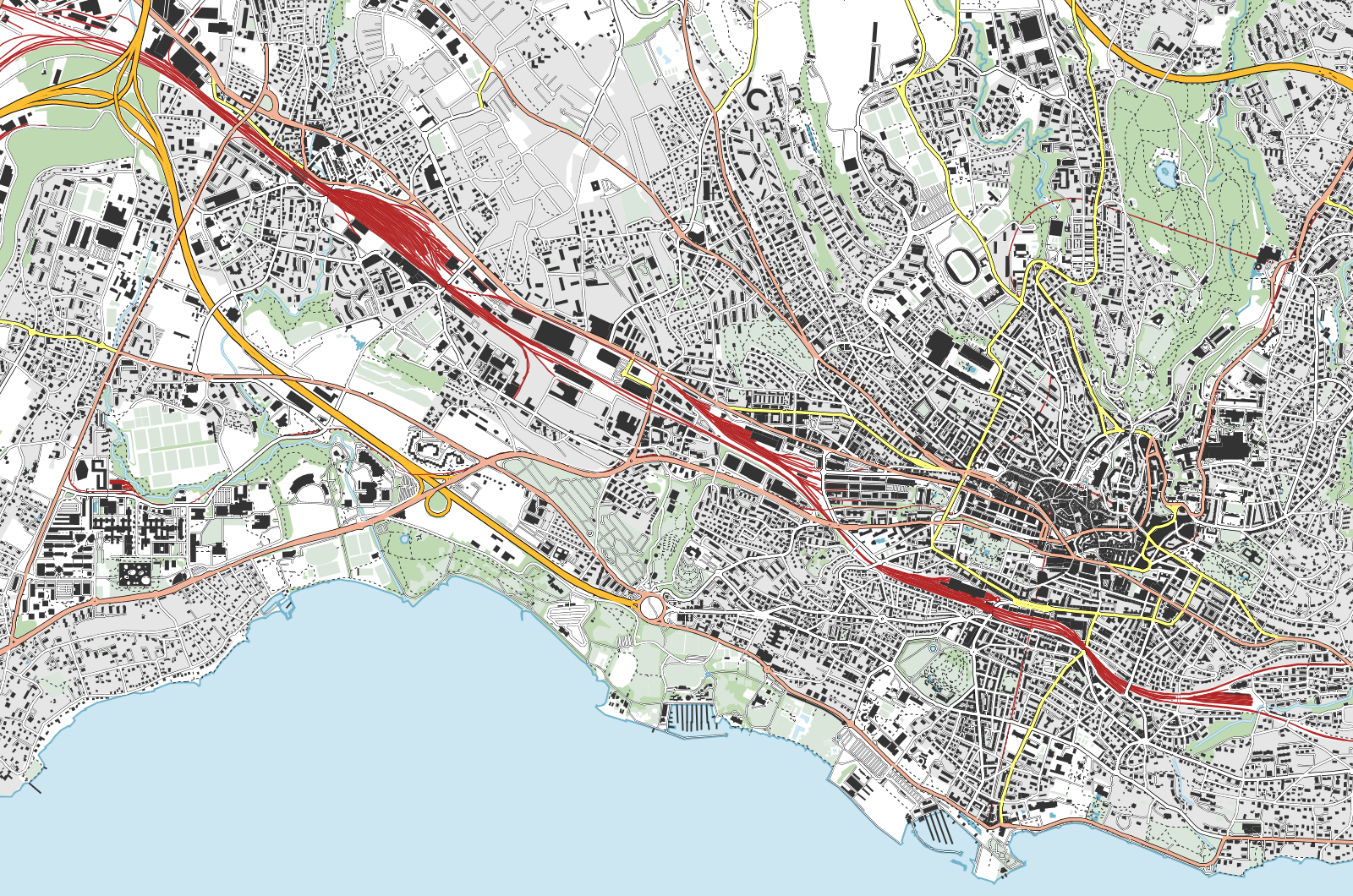
Figure 3 : Lausanne et sa région à 150 dpi
La seconde image est celle d'une carte d'Interlaken et sa région, de 800 par 530 pixels, à une résolution de 72 dpi, présentée ci-dessous et disponible également en version originale. Dans les système CH1903, les coordonnées du coin bas-gauche sont (628590, 168210) et celles du coin haut-droite sont (635660, 172870).
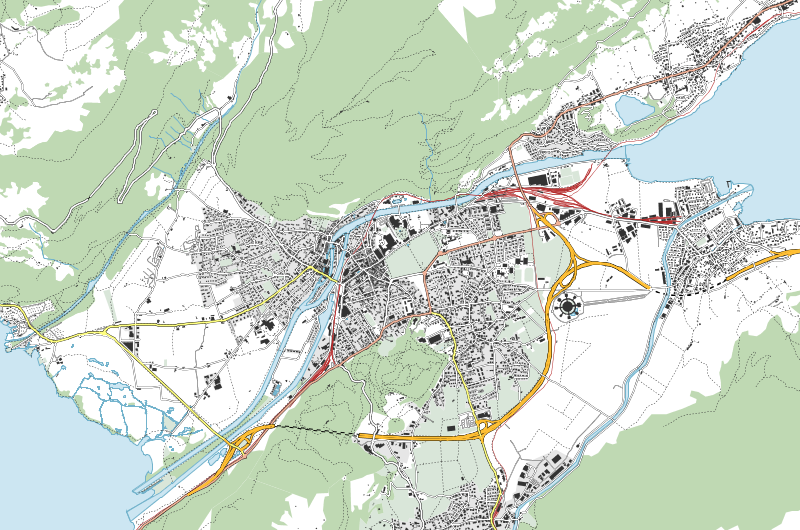
Figure 4 : Interlaken et sa région à 72 dpi
Nous avons également dessiné ces deux cartes sans activer l'anticrénelage afin de faciliter vos tests. Les résultats, fort peu plaisants, sont disponibles ci-dessous :
3 Résumé
Pour cette étape, vous devez :
- écrire les classes représentant un générateur de peintre de réseau routier et un vecteur tridimensionnel, selon les spécifications données plus haut,
- vérifier que vous obtenez les mêmes images des carte de Lausanne et Interlaken que celles que nous vous fournissons,
- documenter la totalité des entités publiques que vous avez définies.
Aucun rendu n'est à faire pour cette étape.