Etape 8 – Toiles et peintres
1 Introduction
Le but de cette étape est d'écrire les classes de dessin de carte, basées sur les notions de toile et de peintre, décrites ci-dessous. Une fois cette étape terminée, vous devriez être capables de dessiner votre première carte et voir ainsi vos efforts des semaines précédentes récompensés !
1.1 Toiles
En informatique, le terme de toile (canvas en anglais) est souvent utilisé pour désigner une surface virtuelle sur laquelle il est possible de dessiner. Contrairement aux toiles réelles, totalement passives, les toiles virtuelles sont généralement actives et savent « se dessiner dessus ». Par exemple, il suffit de dire à une toile virtuelle que l'on désire dessiner un cercle de couleur, rayon et centre donnés pour qu'elle s'exécute et mette son état à jour en fonction.
Le dessin des cartes du projet se fait sur une toile virtuelle représentant une zone rectangulaire du plan, identifiée par les coordonnées de ses coins bas-gauche et haut-droit. Au moment de sa création, une toile est uniformément colorée avec une couleur de fond donnée.
Une telle toile vierge est présentée dans la figure ci-dessous, annotée avec les axes du plan et les points PBL (pour bottom-left) et PTR (pour top-right) désignant deux coins opposés de la zone du plan couverte par la toile.
Figure 1 : Une toile vierge de couleur blanche
Les toiles de ce projet sont relativement simples, dans le sens où elles ne savent dessiner que les deux types de primitives géométriques qui nous intéressent, à savoir les polylignes et les polygones à trous. Le dessin de chacune de ces primitives est toutefois paramétrable de différentes manières, comme cela a été expliqué lors de l'étape précédente.
Toiles concrètes
Il est possible d'imaginer plusieurs mises en œuvre concrètes du concept de toile décrit ci-dessus.
Par exemple, un premier type de toile concrète pourrait directement afficher à l'écran les primitives qu'on lui demande de dessiner ; un second pourrait stocker ces primitives dans un fichier PDF pour affichage ultérieur ; et ainsi de suite.
Pour ce projet, le seul type de toile concrète qu'il vous est demandé d'écrire dessine dans une image discrète, c-à-d un tableau bidimensionnel de pixels. Dès lors, en plus des attributs mentionnés plus haut et communs à tous les types de toiles — zone du plan couverte et couleur de fond — ce type de toile possède les attributs suivants :
- les dimensions en pixels (largeur et hauteur) de l'image,
- la résolution de l'image, c-à-d le nombre de pixels par unité de longueur.
En informatique, la résolution d'une image est souvent spécifiée en points par pouces (dots per inch en anglais, communément abrégé dpi), qui donne le nombre de pixels par pouce1. Par exemple, étant donné qu'un pouce correspond à 2.54 cm, une résolution de 600 dpi correspond à environ 236 pixels par centimètre.
La résolution est nécessaire pour transformer les dimensions exprimées en unités physiques en pixels. Ainsi, même si cela n'a pas été mentionné explicitement dans l'énoncé de l'étape précédente, la largeur du trait d'une polyligne est spécifiée en points pica. Comme le point pica est une unité de longueur physique, valant un peu plus de 1/3 de mm, le nombre de pixels correspondant à un point pica dépend bien entendu de la résolution de l'image.
1.2 Peintres
En informatique, on désigne parfois par le terme de peintre (painter en anglais) l'entité chargée de dessiner sur une toile virtuelle.
On l'a vu, les toiles virtuelles sont plus actives que les toiles réelles et, pour compenser, les peintres virtuels sont moins actifs que leurs homologues réels. C'est-à-dire qu'ils ne modifient pas directement l'état de la toile sur laquelle ils dessinent, mais se contentent de lui demander de dessiner certaines primitives avec un style donné.
Les peintres de ce projet sont des peintres de carte qui, étant donnés une carte et une toile, dessinent cette première sur cette dernière selon une technique qui leur est propre.
La création de peintre de cartes se fait en utilisant une approche — parfois qualifiée de compositionnelle ou d'algébrique — similaire à celle utilisée pour créer les flots Java (interface Stream) ou les images continues de la série 5.
Dans cette approche, plutôt que de définir des peintres monolithiques sophistiqués, capables p.ex. de dessiner une carte telle que celle donnée dans le document d'introduction au projet, on définit d'une part des peintres très simples, appelés peintres de base, et d'autre part des opérations de dérivation ou de combinaison permettant d'obtenir de nouveaux peintres à partir de peintres existants. Un peintre sophistiqué s'obtient ensuite en appliquant ces opérations à des peintres simples.
Les peintres de base sont au nombre de trois :
- un peintre de polygone, qui peint l'intérieur de tous les polygones de la carte avec une couleur donnée,
- un peintre de polyligne, qui peint toutes les polylignes de la carte avec un style de ligne donné,
- un peintre de pourtour, qui peint toutes les polylignes formant les enveloppes et les trous des polygones de la carte avec un style de ligne donné.
Deux opérations, que nous qualifierons d'opérations de dérivation ou de combinaison, permettent d'obtenir un nouveau peintre à partir de peintres existants :
- le filtrage, qui consiste à obtenir un nouveau peintre à partir d'un peintre existant en ne fournissant à ce dernier qu'un sous-ensemble des entités de la carte à dessiner,
- l'empilement, qui consiste à combiner deux peintres pour en obtenir un nouveau dessinant tout d'abord la carte du premire peintre puis, par dessus, la carte du second.
En utilisant judicieusement les peintres de base et ces opérations de dérivation, il est possible d'obtenir des peintres composites ayant un comportement aussi sophistiqué que nécessaire. Par exemple, il est facile d'obtenir un peintre ne dessinant que les lacs, en bleu, et les bâtiments, en noir :
- un premier peintre de polygone paramétré avec la couleur bleue est créé,
- ce premier peintre est filtré dans le but de ne voir que les entités de la carte possédant l'attribut
naturalavec la valeurwater, - un second peintre de polygone paramétré avec la couleur noire est créé,
- ce second peintre est filtré dans le but de ne voir que les entités de la carte possédant l'attribut
building, quelle que soit la valeur associée, - le second peintre filtré est empilé sur le premier peintre filtré pour obtenir le peintre final.
En procédant de manière similaire, on peut obtenir sans trop de difficultés un peintre capable de dessiner des cartes aussi détaillées que celle d'Interlaken présentée dans le document d'introduction au projet.
2 Mise en œuvre Java
Il est conseillé de placer les classes et interfaces décrites ci-dessous dans le paquetage dédié au dessin, que l'énoncé de l'étape précédente suggérait de nommer ch.epfl.imhof.painting.
2.1 Toile
La première interface à définir, nommée p.ex. Canvas, représente une toile. Elle est extrêmement simple et ne contient que deux méthodes (abstraites) :
- une méthode, nommée p.ex.
drawPolyLine, permettant de dessiner sur la toile une polyligne donnée (de typePolyLine) avec un style de ligne donné (du type défini lors de l'étape précédente), - une méthode, nommée p.ex.
drawPolygon, permettant de dessiner sur la toile un polygone donné (de typePolygon) avec une couleur donnée (du type défini lors de l'étape précédente).
2.2 Toile Java2D
Comme cela a été dit plus haut, la seule mise en œuvre concrète de toile à écrire dessine les primitives qu'on lui demande de dessiner dans une image discrète. Ce dessin étant loin d'être trivial, il sera fait à l'aide d'une partie de la bibliothèque Java nommée Java2D et décrite rapidement à la section suivante.
Cette mise en œuvre concrète de la toile se fait naturellement dans une classe implémentant l'interface des toiles définie ci-dessus et nommée p.ex. Java2DCanvas. Son constructeur prend les arguments suivants :
- les points, en coordonnées du plan (donc les coordonnées projetées), correspondant aux coins bas-gauche et haut-droite de la toile,
- la largeur et la hauteur de l'image de la toile, en pixels,
- la résolution de l'image de la toile, en points par pouce,
- la couleur de fond de la toile.
En plus des méthodes drawPolyLine et drawPolygon, cette classe doit offrir une méthode, nommée p.ex. image, permettant d'obtenir l'image de la toile, de type BufferedImage.
Il est fortement conseillé, dans le constructeur de cette classe, d'utiliser la méthode de changement de repère écrite lors de l'étape précédente pour calculer le changement entre le repère du plan et celui de l'image, et de le stocker dans un attribut. Cela simplifie l'écriture des méthodes drawPolyLine et drawPolygon, qui peuvent l'utiliser pour transformer les coordonnées des points des lignes ou polygones qu'elles reçoivent en coordonnées à passer aux méthodes de Java2D.
2.3 Java2D
Java2D est constitué d'un ensemble de classes permettant de dessiner et manipuler des images en deux dimensions (2D). Pour des raisons historiques, ces classes se trouvent dans le paquetage nommé java.awt (AWT signifiant Abstract Window Toolkit) et ses sous-paquetages.
La plupart des concepts de Java2D sont identiques à ceux du langage de description de page PostScript, prédécesseur du format PDF développé dans les années 80 par Adobe. Ce langage offrait un modèle graphique 2D d'une très grande sophistication pour l'époque, dont l'influence a été telle qu'aujourd'hui encore la plupart des modèles graphiques 2D — p.ex. celui de SVG ou encore de l'élément canvas de HTML 5 — s'en inspirent très largement.
Seul un petit sous-ensemble de concepts de Java2D est nécessaire pour écrire la classe ci-dessus, et est décrit succinctement ci-dessous. Pour comprendre en détail le fonctionnement des différentes classes et méthodes, reportez-vous à leur documentation en suivant les liens donnés et étudiez l'exemple donné plus bas.
Images
Une image (discrète et finie, pour reprendre la terminologie de la série 5) est représentée par la classe abstraite Image. La seule sous-classe concrète qui nous intéresse ici est BufferedImage, qui représente une image stockée en mémoire sous la forme d'un tableau bidimensionnel de pixels. Pour mémoire, un pixel est un point (au sens mathématique, donc sans dimensions) dont on connaît la couleur.
Une image BufferedImage peut utiliser différentes représentations pour les couleurs des pixels, en fonction d'un paramètre passé à son constructeur. Pour ce projet, nous utiliserons uniquement celle désignée par la constante TYPE_INT_RGB. Même s'il n'est pas nécessaire que vous compreniez en détail cette représentation, sachez qu'elle consiste à stocker les trois composantes des couleurs dans un entier de type int, en plaçant la composante rouge dans les bits 23 à 16, la verte dans les bits 15 à 8, et la bleue dans les bits 7 à 0.
Le repère d'une image a son origine dans le coin haut-gauche de celle-ci, et l'axe des abscisses est dirigé vers la droite tandis que celui des ordonnées est dirigé vers le bas. De plus, les pixels sont, par convention, espacés de 1 point pica. Dès lors, le coin bas-droite d'une image a les coordonnées (w, h) où w est sa largeur en pixels, h sa hauteur en pixels. Ces conventions sont illustrées dans l'image ci-dessous, reprise de la série 5.
Figure 2 : Repère des images AWT
Contexte graphique
Un contexte graphique est un objet stockant tous les paramètres relatifs au dessin — p.ex. la couleur de dessin — et offrant d'une part des méthodes permettant de connaître et de modifier ces paramètres et d'autre part des méthodes permettant de dessiner.
Pour des raisons historiques, deux classes sont utilisées pour représenter les contextes graphiques dans Java2D, Graphics et Graphics2D. La seconde, plus récente et dotée de plus d'attributs que la première dont elle hérite, est la seule utilisée dans ce projet.
De nombreux paramètres de dessin sont définis par la classe Graphics2D, mais seul un petit sous-ensemble nous intéresse ici, composé de :
- la couleur de dessin (méthodes
getColoretsetColor), - le type de trait (méthodes
setStrokeetgetStroke), décrit à la section suivante, - la transformation géométrique (méthode
scaleet d'autres qui ne nous intéressent pas), - l'anticrénelage (méthode
setRenderingHintà laquelle il faut passer la valeurKEY_ANTIALIASINGcomme clef, et la valeurVALUE_ANTIALIAS_ONcomme valeur pour l'activer).
La transformation géométrique attachée au contexte est systématiquement appliquée aux éléments dessinés à travers lui. Par exemple, si la transformation est une rotation autour de l'origine, alors tous les éléments subissent cette rotation avant d'être dessinés. Par défaut, la transformation attachée à un contexte est l'identité, donc les éléments sont dessinés sans transformation.
L'anticrénelage (anti-aliasing en anglais), dont le principe de fonctionnement ne sera pas détaillé ici, permet d'améliorer sensiblement la qualité du dessin. Etant donné qu'il n'est pas activé par défaut, il faut impérativement le faire dès le contexte graphique créé.
En plus des méthodes permettant d'accéder aux paramètres de dessin, la classe Graphics2D offre un grand nombre de méthodes de dessin. Seules les méthodes suivantes nous seront utiles :
- la méthode
fillRect, permettant de remplir un rectangle au moyen de la couleur de dessin actuelle, - la méthode
draw, permettant de dessiner le pourtour d'une forme (concept décrit plus bas) avec la couleur de dessin et le trait actuels, - la méthode
fill, permettant de remplir une forme avec la couleur de dessin actuelle.
Pour dessiner dans une image de type BufferedImage, il faut obtenir un contexte graphique pour elle, ce qui peut se faire au moyen de sa méthode createGraphics.
Traits
L'interface Stroke représente une manière de dessiner le pourtour d'une forme géométrique.
Dans le cadre de ce projet, la seule implémentation de cette interface qui nous intéresse est la classe BasicStroke. Cette classe permet de dessiner le pourtour d'une forme géométrique au moyen des mêmes paramètres que ceux que nous avons regroupés dans le style de dessin des polylignes à l'étape précédente.
A noter que deux paramètres peu importants de BasicStroke n'ont pas d'équivalent dans le style de dessin défini à l'étape précédente. Il s'agit de ceux nommés miterlimit et dashPhase (voir le constructeur principal de BasicStroke), pour lesquels vous utiliserez les valeurs par défaut de 10.0 et 0, respectivement.
Formes
L'interface Shape représente une forme géométrique. Deux types de formes suffisent pour dessiner les polylignes et les polygones à trous, qui sont représentées par deux classes implémentant cette interface :
Path2D(et sa sous-classePath2D.Double), qui représente un chemin, c-à-d une séquence de points qui ressemble à ce que nous avons nommé une polyligne, etArea, qui représente une surface, p.ex. un polygone à trous.
Pour obtenir le chemin correspondant à une polyligne, il suffit de créer un nouveau chemin, d'appeler la méthode moveTo pour ajouter le point initial de la polyligne, puis d'appeler la méthode lineTo pour les autres points. Finalement, si la polyligne est fermé, il faut fermer le chemin au moyen de la méthode closePath.
Pour obtenir la surface correspondant à un polygone à trous, il suffit de transformer l'enveloppe en chemin puis de la passer au bon constructeur de Area, puis ensuite de soustraire chacun des trous au moyen de la méthode subtract.
Résolution
Comme cela a été mentionné plus haut, l'espacement entre les pixels de la classe BufferedImage est fixé à 1 point pica. Etant donné qu'il y a 72 points pica par pouce, cela revient à fixer la résolution de ces images à 72 dpi.
Cette résolution fixe ne nous convient pas, car nous désirons pouvoir produire une images à une résolution quelconque. Malheureusement, Java2D n'offre pas de moyen direct de changer la résolution d'une image BufferedImage, mais il est possible d'utiliser la transformation associée à son contexte graphique pour contourner ce problème, en dilatant les éléments dessinés.
Nous vous suggérons donc de procéder ainsi dans le constructeur de la classe des toiles Java2D :
- une fois l'image de la toile créée et son contexte obtenu, changer la transformation attachée à ce dernier (via la méthode
scale) pour en faire une dilatation d'un facteur égal à la résolution de l'image divisée par 72 ; ainsi, la largeur des traits et la longueur des segments opaques et transparent sera automatiquement adaptée lors du dessin dans le contexte, - tenir compte de cette dilatation lors du calcul du changement de repère.
Exemple
Le programme d'exemple ci-dessous utilise plusieurs des classes et méthodes de Java2D décrites ci-dessus pour dessiner un drapeau suisse. Il devrait faciliter la compréhension de l'ensemble.
import java.awt.Color; import java.awt.Graphics2D; import java.awt.geom.Path2D; import java.awt.image.BufferedImage; import java.io.File; import java.io.IOException; import javax.imageio.ImageIO; import static java.awt.RenderingHints.KEY_ANTIALIASING; import static java.awt.RenderingHints.VALUE_ANTIALIAS_ON; public final class SwissFlag { public static final int SIZE = 200; public static void main(String[] args) throws IOException { BufferedImage image = new BufferedImage(SIZE, SIZE, BufferedImage.TYPE_INT_ARGB); Graphics2D ctx = image.createGraphics(); // Active l'anticrénelage. ctx.setRenderingHint(KEY_ANTIALIASING, VALUE_ANTIALIAS_ON); // Remplit le fond en rouge. ctx.setColor(Color.RED); ctx.fillRect(0, 0, SIZE, SIZE); // Change le repère pour que chaque côté soit // de longueur unitaire… ctx.scale(SIZE, SIZE); // …et l'origine au centre. ctx.translate(0.5, 0.5); // Dessine deux rectangles tournés de 90° pour // obtenir la croix. ctx.setColor(Color.WHITE); for (int i = 0; i < 2; ++i) { Path2D rect = new Path2D.Double(); rect.moveTo(-0.1, -0.3); rect.lineTo(0.1, -0.3); rect.lineTo(0.1, 0.3); rect.lineTo(-0.1, 0.3); rect.closePath(); ctx.fill(rect); ctx.rotate(Math.PI / 2d); } // Ecrit le résultat au format PNG dans un fichier. ImageIO.write(image, "png", new File("ch.png")); } }
En exécutant ce programme, on obtient l'image ci-dessous.

Figure 3 : Le drapeau suisse, par Java2D
2.4 Peintre
La seconde interface à définir est une interface fonctionnelle, nommée p.ex. Painter, représentant un peintre. Sa méthode abstraite, nommée p.ex. drawMap, prend en argument une carte et une toile, son but étant de dessiner la première sur la seconde.
En dehors de sa méthode abstraite, l'interface des peintres offre un certain nombre de méthodes statiques permettant d'obtenir des peintres de base de l'un des trois types décrits plus haut — polygone, polyligne ou pourtour. Nous vous proposons d'offrir un total de sept méthodes :
- la première, nommée p.ex.
polygon, prend en argument la couleur de dessin et retourne un peintre dessinant l'intérieur de tous les polygones de la carte qu'il reçoit avec cette couleur, - la deuxième, nommée p.ex.
line, prend en argument un style de ligne (du type défini à l'étape précédente) et retourne un peintre dessinant toutes les lignes de la carte qu'on lui fournit avec ce style, - la troisième, nommée de la même manière que la deuxième, prend en arguments les cinq paramètres de dessin d'une ligne et retourne un peintre dessinant toutes les lignes de la carte qu'on lui fournit avec le style correspondant,
- la quatrième, nommée de la même manière que la deuxième, ne prend en argument que la largeur du trait et la couleur et utilise les valeurs par défaut données dans l'étape précédente pour les autres paramètres de style,
- la cinquième, nommée p.ex.
outline, est identique à la deuxième mais dessine les pourtours de l'enveloppe et des trous de tous les polygones de la carte qu'on lui fournit, - la sixième est l'équivalent de la troisième pour la cinquième,
- la septième est l'équivalent de la quatrième pour la cinquième.
De plus, l'interface des peintres offre trois méthodes par défaut permettant d'obtenir des peintres dérivés de peintres existants :
- une méthode nommée p.ex.
whenprenant en argument un prédicat de typePredicate<Attributed<?>>et retournant un peintre se comportant comme celui auquel on l'applique, si ce n'est qu'il ne considère que les éléments de la carte satisfaisant le prédicat, - une méthode nommée p.ex.
aboveprenant en argument un autre peintre et retournant un peintre dessinant d'abord la carte produite par ce second peintre puis, par dessus, la carte produite par le premier peintre, - une méthode nommée p.ex.
layeredne prenant aucun argument et retournant un peintre utilisant l'attributlayerattaché aux entités de la carte pour la dessiner par couches, c-à-d en dessinant d'abord tous les entités de la couche –5, puis celle de la couche –4, et ainsi de suite jusqu'à la couche +5.
Réfléchissez bien avant de programmer ces méthodes, dont le code est court (entre 5 et 10 lignes au maximum) mais pas évident à écrire. De plus, n'hésitez pas à utiliser les méthodes when et above ainsi que le filtre produit par la méthode onLayer de l'étape précédente pour écrire la méthode layered.
Notez finalement que les peintres étant représentés par une interface fonctionnelle, l'utilisation judicieuse de fonctions anonymes (lambdas) permet de réduire considérablement la quantité de code à écrire.
2.5 Exemple
Le fonctionnement des peintres, filtres et toiles n'étant pas des plus évidents à comprendre, un exemple de leur utilisation permet de clarifier les choses. L'extrait de programme ci-dessous construit, en s'aidant des classes définies à l'étape précédente, le peintre décrit plus haut et l'utilise pour dessiner une carte très simple de Lausanne et sa région.
// Le peintre et ses filtres Predicate<Attributed<?>> isLake = Filters.tagged("natural", "water"); Painter lakesPainter = Painter.polygon(Color.BLUE).when(isLake); Predicate<Attributed<?>> isBuilding = Filters.tagged("building"); Painter buildingsPainter = Painter.polygon(Color.BLACK).when(isBuilding); Painter painter = buildingsPainter.above(lakesPainter); Map map = …; // Lue depuis lausanne.osm.gz // La toile Point bl = new Point(532510, 150590); Point tr = new Point(539570, 155260); Java2DCanvas canvas = new Java2DCanvas(bl, tr, 800, 530, 72, Color.WHITE); // Dessin de la carte et stockage dans un fichier painter.drawMap(map, canvas); ImageIO.write(canvas.image(), "png", new File("loz.png"));
L'image obtenue est la suivante :
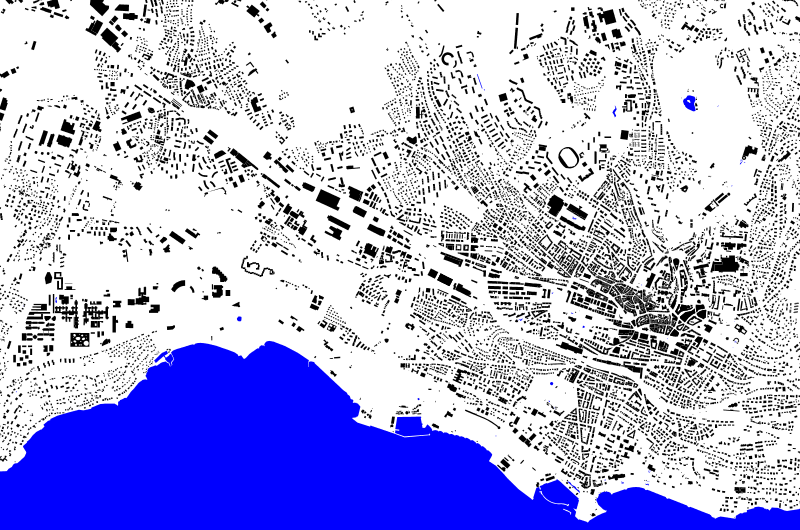
Figure 4 : Lausanne et sa région en noir, bleu et blanc
2.6 Tests
Pour tester cette étape et la précédente, nous vous conseillons d'écrire un petit programme principal permettant de dessiner, dans un fichier, la carte de Lausanne donnée en exemple ci-dessus.
Attention : l'image visible plus haut est redimensionnée par votre navigateur afin de tenir dans les marges de ce document, donc pour comparer l'image que vous obtenez avec la nôtre, pensez à télécharger cette dernière sur votre ordinateur via ce lien.
3 Résumé
Pour cette étape, vous devez :
- écrire les classes et interfaces représentant une toile, une toile Java2D et un peintre, selon les spécifications données plus haut,
- vérifier que vous obtenez la même image de carte de Lausanne que celle que nous vous fournissons,
- documenter la totalité des entités publiques que vous avez définies.
Aucun rendu n'est à faire pour cette étape.
Notes de bas de page
Notez que le terme résolution est souvent utilisé de manière incorrecte pour parler de la taille en pixels d'une image, d'un capteur ou d'un écran. Par exemple, on parle d'un écran ayant « une résolution de 1920 par 1080 pixels ». Cela est incorrect car la résolution spécifie la densité de pixels, et s'exprime en pixels par unité de longueur, pas en pixels. Pour éviter toute confusion, le terme résolution est toujours utilisé pour désigner une densité de pixels dans ce document.