Série 6 – Images continues génériques
Introduction
Le but de cette série est de continuer le miniprojet images continues commencé la semaine dernière, en utilisant la généricité pour généraliser la notion d'image. Votre point de départ sera donc soit votre propre version de la série 5, soit le code de notre corrigé.
Il peut être judicieux de commencer un nouveau projet Eclipse pour cette série plutôt que de modifier celui de la série précédente, afin de pouvoir au besoin passer de l'un à l'autre et voir les changements.
Exercice 1
Lors de la première partie de ce miniprojet, nous avions défini une image comme étant une fonction qui, étant donné un point dans le plan, retourne la couleur de ce point. En Java, nous avions exprimé cela au moyen de l'interface fonctionnelle ImageRGB suivante :
public interface ImageRGB { public ColorRGB valueAt(double x, double y); }
Le but de ce premier exercice est de généraliser ce concept, en définissant une image comme une fonction qui, étant donné un point, retourne non plus une couleur mais une valeur d'un type arbitraire. L'intérêt de cette généralisation deviendra apparent dans les exercices suivants, le seul but de celui-ci étant de faire les modifications qui s'imposent dans le code.
La première chose à faire est de modifier l'interface ImageRGB afin de la généraliser comme expliqué ci-dessus. Pour exprimer le fait qu'une image est une fonction qui, étant donné un point, retourne une valeur d'un type quelconque, on utilise bien entendu la généricité. La nouvelle version de l'interface ImageRGB, renommée1 au passage Image, se présente donc ainsi :
public interface Image<T> { public T valueAt(double x, double y); }
Une fois cette modification effectuée, il faut bien entendu modifier tout le code existant qui utilisait ImageRGB pour tenir compte du fait que Image est maintenant générique.
Ce faisant, on constate que toutes les méthodes qui produisent des images, comme chessboard ou target, doivent avoir Image<ColorRGB> comme type de retour. Par contre, les méthodes de transformation comme rotated, qui transforment de manière purement géométrique l'image à laquelle on les applique, ont Image<T> comme type de retour.
Une fois les modifications effectuées, assurez-vous d'une part qu'Eclipse ne produit plus aucun avertissement, et d'autre part que le programme est toujours capable d'afficher une image de votre choix.
Exercice 2
Ayant généralisé la notion d'image, il devient possible de définir des images produisant autre chose que des couleurs. Bien entendu, de telles « images » ne sont pas directement affichables à l'écran, mais elles peuvent être très utiles néanmoins comme nous le verrons à l'exercice suivant.
La première image « non colorée » à définir est une simplification du dégradé linéaire de la série précédente. La nouvelle méthode qui la produit, nommée linearHorizontalGradientMask, est une image de valeurs réelles. C'est-à-dire qu'elle a le type Image<Double> et sa méthode valueAt retourne simplement la valeur de la proportion du mélange, appelée \(p\) la semaine dernière. Sous forme mathématique, cette « image » se présente ainsi :
Bien entendu, étant donné que cette image ne produit plus de couleur, la méthode linearHorizontalGradientMask ne prend en paramètre que les deux limites du dégradé, \(x_l\) et \(x_r\).
Une telle image, qui associe une valeur réelle comprise entre 0 et 1 à chaque point du plan, est appelée un masque ou encore un canal alpha dans des programmes comme Photoshop. Ces masques peuvent être utilisés pour mélanger deux images entre elles, et le masque détermine alors, pour chaque point, la proportion du mélange des images.
Exercice 3
Une fois le masque dégradé linéaire défini, il vous est maintenant possible de définir une méthode de composition de deux images au moyen d'un masque. Cette méthode, nommée compose, retourne une valeur de type Image<ColorRGB> et prend trois arguments : une image d'arrière-plan de type Image<ColorRGB>, une image d'avant-plan de même type et un masque de type Image<Double>. Sa méthode valueAt est définie de manière à ce que la couleur d'un point de l'image finale soit un mélange de la couleur de l'image d'arrière-plan avec la proportion donnée par le masque de la couleur de l'image d'avant-plan.
En termes mathématiques, et en réutilisant la notation du corrigé de la série précédente, cette classe de composition calcule la couleur de \(c\) de l'image finale ainsi, si \(b\) est l'image d'arrière-plan (background), \(f\) celle d'avant-plan (foreground) et \(m\) le masque :
\begin{displaymath} c(x, y) = b(x, y) \oplus_{m(x,y)} f(x,y) \end{displaymath}Autrement dit, l'image finale est égale à l'arrière-plan partout où le masque vaut 0, égale à l'avant-plan partout où le masque vaut 1, et un mélange des deux lorsque le masque vaut quelque chose entre 0 et 1.
Une fois cette méthode définie, on peut l'utiliser pour composer un arrière-plan, formé d'un échiquier de cellules blanches et grises de 0.2 unités de côté, avec un avant-plan, la photo de Dubrovnik fournie, le tout au moyen d'un masque dégradé linéaire allant de –0.3 à 0.3. On obtient le résultat ci-dessous, aux qualités artistiques discutables, mais néanmoins intéressant.
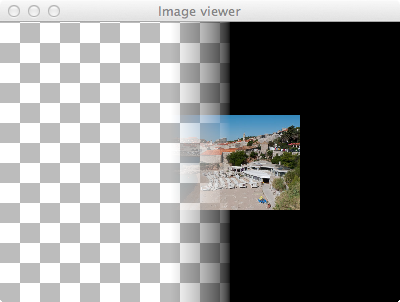
Figure 1 : Dubrovnik masquée
Les méthodes de transformation comme rotated étant génériques, il est possible de les appliquer aux masques comme aux images couleur. En appliquant le transformateur de rotation au masque pour le faire tourner de 45°, on obtient ainsi l'image ci-dessous.
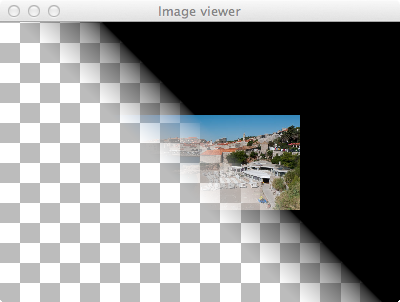
Figure 2 : Dubrovnik masquée (v2)
Exercice 4
Pour terminer, définissez une méthode permettant d'obtenir la fameuse image (fractale) de l'ensemble de Mandelbrot. Cet ensemble est défini comme étant celui des points \(c\) du plan complexe pour lesquels la suite définie par :
\begin{displaymath} \begin{align} z_0 &= 0\\ z_{n+1} &= z_n^2 + c \end{align} \end{displaymath}est bornée, c-à-d qu'elle ne tend pas vers l'infini.
En pratique, pour déterminer si un point \(c\) du plan complexe appartient ou non à l'ensemble de Mandelbrot, on utilise une méthode approximative consistant à calculer les \(m\) premiers termes de la suite ci-dessus. Si au moins un terme de cette suite finie a un module supérieur ou égal à 2, alors on a la garantie que la suite est croissante à partir de ce terme, et donc que le point n'appartient pas à l'ensemble de Mandelbrot. Par contre, si tous les termes de cette suite finie ont un module inférieur à 2, on fait l'hypothèse que le point appartient à l'ensemble de Mandelbrot.
Par exemple, pour l'origine, \(c = 0 + 0i\) et il est évident que tous les termes de la suite ci-dessus valent 0. Dès lors, on arrête le calcul de ces termes après en avoir calculé le nombre maximum \(m\) et, étant donné qu'aucun d'entre-eux n'a un module supérieur ou égal à 2, on en conclut que l'origine fait partie de l'ensemble de Mandelbrot.
La méthode à écrire, nommée p.ex. mandelbrotSet, prend en argument le nombre maximum \(m\) de termes de la suite à calculer — utilisez 100 pour les tests — et retourne une image booléenne de type Image<Boolean>. Le booléen associé à chaque point n'est vrai que si le point en question — interprété comme un nombre complexe — appartient à l'ensemble de Mandelbrot.
Pour transformer une image booléenne en image affichable de type Image<ColorRGB>, vous pouvez ajouter une méthode très simple à la classe Image qui, étant donné une image booléenne et deux couleurs, produit une image en couleur telle que tous les points pour lesquels l'image booléenne est vraie sont dessinés avec la première couleur, les autres avec la seconde.
Pour simplifier la définition de l'image de l'ensemble de Mandelbrot, vous pouvez bien entendu définir une classe très simple représentant un nombre complexe et dotée uniquement des méthodes utiles ici, à savoir l'addition, l'élévation au carré et le calcul du module.
Note : l'image de l'ensemble de Mandelbrot peut se définir de manière élégante au moyen de la programmation par flots, mais cela nécessite l'utilisation d'une méthode de l'interface Stream que nous n'avons pas vue au cours. N'hésitez donc pas à lire la documentation de cette interface si vous désirez suivre cette voie.
Notes de bas de page
Notez que, dans Eclipse, il est très simple de renommer l'interface ImageRGB en Image. Il suffit de placer le curseur sur le nom de cette interface, puis de choisir l'entrée Rename du menu Refactor et d'entrer le nouveau nom, ici Image. Cela fait, Eclipse trouve et renomme toutes les occurrences de ImageRGB en Image dans le projet, et renomme également le fichier de ImageRGB.java en Image.java.