Série 11 – Piles immuables

Le but de cette série est d'explorer le thème de l'immuabilité à travers une mise en œuvre immuable d'une collection que vous connaissez déjà, les piles. Pour vous permettre de démarrer nous vous fournissons une archive Zip contenant l'interface Stack présentée ci-dessous, un squelette de mise en œuvre des piles immuables et un programme graphique décrit plus bas.

Comme nous l'avons vu au cours, les collections non modifiables diffèrent des collections modifiables de par le fait que les opérations qui ajoutent ou suppriment des éléments retournent toutes une nouvelle collection. C'est obligatoire, puisque par définition les collections immuables ne peuvent être modifiées ! Pour les piles immuables, une interface appropriée pourrait donc être :

public interface Stack<E> {
    // Vrai ssi la pile est vide.
    public boolean isEmpty();

    // Retourne la taille de la pile.
    public int size();

    // Retourne une nouvelle pile avec les mêmes éléments que
    // this, mais newElem en plus au sommet.
    public Stack<E> push(E newElem);

    // Retourne une nouvelle pile avec les mêmes éléments que
    // this, sans celui du sommet. Lève EmptyStackException
    // si la pile est vide.
    public Stack<E> pop();

    // Retourne le sommet de la pile. Lève EmptyStackException
    // si la pile est vide.
    public E top();
}

La différence cruciale entre cette interface et celle d'une pile modifiable est que les méthodes qui devraient modifier la pile (ici push et pop) ne la modifient pas mais retournent une nouvelle pile. Dans le cas de push, la pile retournée a les mêmes éléments que la pile originale si ce n'est qu'un élément supplémentaire se trouve au sommet de cette nouvelle pile. Dans le cas de pop, la pile retournée est semblable à la pile originale mais avec l'élément de tête en moins. Bien entendu, pop et top lèvent l'exception java.util.EmptyStackException lorsqu'on les applique à une pile vide.

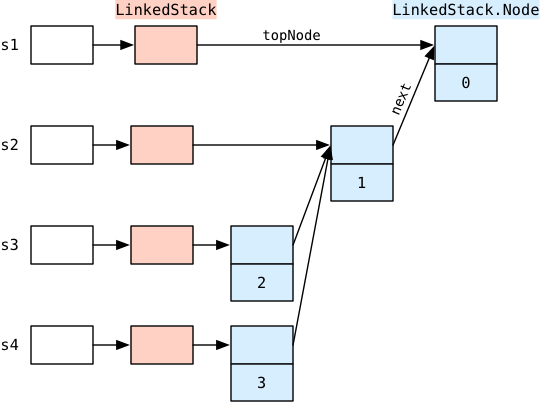
Les piles ressemblant beaucoup aux listes, on utilise généralement les mêmes techniques de mise en œuvre pour les deux. Pour cet exercice, nous vous demandons d'utiliser la technique du chaînage simple. En d'autres termes, la classe modélisant les piles contient une référence vers le nœud du sommet, et chaque nœud contient une référence vers son successeur, éventuellement inexistant. Notez que comme ces piles sont immuables, il n'y a aucun problème pour que différentes piles partagent des nœuds entre-elles. Ainsi, si on exécute le morceau de programme ci-dessous :

Stack<Integer> s1 = LinkedStack.<Integer>emptyStack().push(0);
Stack<Integer> s2 = s1.push(1);
Stack<Integer> s3 = s2.push(2);
Stack<Integer> s4 = s2.push(3);

on devrait obtenir en mémoire la situation illustrée par la figure ci-dessous :

Complétez le squelette de la classe LinkedStack que nous vous fournissons. Pour la tester, vous pouvez soit écrire un test unitaire comme d'habitude, soit passer à l'exercice ci-dessous qui l'utilise pour mettre en œuvre une calculatrice en notation polonaise inverse.

Le programme RPNCalc que nous vous fournissons met en œuvre une calculatrice en notation polonaise inverse, abrégé NPI (reverse Polish notation ou RPN en anglais). Si vous ne connaissez pas encore ce genre de calculatrice, consultez la version anglaise de la page Wikipedia sur la notation polonaise inverse, plus complète que la française.

Une calculatrice en NPI utilise très naturellement une pile pour stocker les valeurs sur lesquelles les calculs sont effectués. Par exemple, pour calculer la valeur de l'expression \((4 + 5) \times (6 + 7)\) avec une telle calculatrice, on appuie successivement sur les touches suivantes — les touches placées entre parenthèses n'étant pas strictement nécessaires mais simplifiant la compréhension :

4, Enter, 5, (Enter), +, 6, Enter, 7, (Enter), +, *

Lors de ce calcul, la pile de la calculatrice évolue ainsi :

Cette pile est stockée dans le champ stack de la classe RPNCalc, qui est naturellement de type Stack<Double>.

En plus de cette pile de valeurs, RPNCalc utilise également une seconde pile, pour mettre en œuvre l'annulation des opérations (undo). En effet, comme cela a été rapidement dit au cours, mettre en œuvre l'annulation est très simple en présence de valeurs immuables, car il suffit de stocker l'historique de ces valeurs et de les restaurer pour annuler les opérations.

Dans le cas de la calculatrice, son état courant est simplement la pile des valeurs mentionnée ci-dessus. Donc pour stocker les versions successives de cet état, on peut simplement les placer dans une collection, qui peut justement être une autre pile ! Cette seconde pile est stockée dans le champ undoStack de la classe, et son type est Stack<Stack<Double>>.

Par exemple, à la fin de l'exécution du calcul ci-dessus, la pile undoStack contient la totalité des piles successives, la plus récente au sommet. En d'autres termes, elle contient la pile de piles suivante (dont le sommet est en bas) :

[ [ 4 ],
  [ 5, 4 ],
  [ 9 ],
  [ 6, 9 ],
  [ 7, 6, 9 ],
  [ 13, 9 ] ]

Remarquez que, à la dernière ligne près (qui correspond à la pile courante à la fin du calcul, qui n'est pas encore stockée dans l'historique), cette pile contient la totalité des piles de la deuxième colonne du tableau plus haut.

Pour annuler une action, il suffit de reprendre la pile qui se trouve au sommet de cette pile de piles et de l'utiliser comme pile de la calculatrice. Ainsi, si à la fin du calcul ci-dessus l'utilisateur clique sur le bouton undo, la pile [ 13, 9 ] est restaurée, comme attendu. S'il clique encore une fois sur undo, c'est la pile [ 7, 6, 9 ] qui est restaurée, et ainsi de suite.

Notez que pour que tout cela fonctionne, il est fondamental que la pile de la calculatrice soit une pile immuable, faute de quoi il faudrait la copier totalement avant de la placer dans la pile d'annulation.

Lisez la totalité du code de la classe RPNCalc pour bien comprendre comment cette pile est gérée et, cela fait, mettez en œuvre l'opération redo. Cette opération permet d'annuler les annulations, et elle se met également en œuvre naturellement au moyen d'une pile de piles. A vous de trouver comment la gérer !