Série 2 – Images continues
Introduction
Cette série d'exercices est la première du mini-projet images continues qui vous permettra, entre autres, d'examiner une application intéressante de la généricité dès la semaine prochaine. Le but de cette série est de servir d'introduction aux différents concepts de ce mini-projet.
Le mini-projet images continues a bien entendu pour thème les images, mais il les représente d'une manière peu habituelle en informatique. En effet, les images numériques sont généralement représentées sous la forme d'un tableau bidimensionnel de points, appelés pixels (pour picture elements), ayant chacun une couleur. Nous qualifierons cette représentation classique des images de discrète et finie puisque la couleur de l'image n'est connue qu'en un nombre fini de points.
La représentation que nous utiliserons pour ce projet est quant à elle continue et infinie. La mémoire d'un ordinateur étant finie, il n'est bien entendu pas possible de représenter directement une telle image par l'ensemble (infini) de ses pixels. Au lieu de cela, on utilise la technique habituellement utilisée en mathématiques, c-à-d qu'on représente une infinité de valeurs au moyen d'une fonction, dont la représentation est, elle, finie.
Par exemple, la fonction mathématique \(f(x) = x^2\), dont la représentation est finie, est composée d'une infinité de paires de valeurs \((x, f(x))\), parmi lesquelles figurent p.ex. (0, 0), (1/2, 1/4) ou encore (12.3, 151.29).
De la même manière, une image peut être vue comme une fonction de deux arguments, les coordonnées x et y d'un point du plan, qui produit une couleur. Par exemple, la fonction suivante est une image d'un disque rouge sur fond blanc, centré à l'origine et de rayon 1 :
\begin{displaymath} f(x, y) = \begin{cases} \color{red}\blacksquare \text{ (rouge)} & \text{si } \sqrt{x^2 + y^2} \le 1\\ \color{white}\blacksquare \text{ (blanc)} & \text{sinon} \end{cases} \end{displaymath}On peut traduire cette idée en Java en définissant une interface pour le concept d'image continue. Cette interface est très simple puisqu'elle ne contient qu'une seule fonction, qui est la fonction qui représente cette image, c-à-d \(f\) dans l'exemple précédent :
public interface ImageRGB { public ColorRGB valueAt(double x, double y); }
Le type ColorRGB est celui d'une classe qui modélise une couleur par le triplet de ses composantes rouges, vertes et bleues (abrégé RGB pour red, green et blue), chacune comprises entre 0 et 1. La valeur 0 représente l'absence d'une composante, tandis que la valeur 1 représente la « présence maximale » de cette composante.
Une fois cette interface définie, il est très simple de traduire la fonction de l'image d'un cercle rouge sur fond blanc donnée plus haut, en définissant une classe implémentant l'interface ImageRGB :
public final class RedWhiteUnitCircle implements ImageRGB { @Override public ColorRGB valueAt(double x, double y) { double r = Math.sqrt(x * x + y * y); return r <= 1.0 ? ColorRGB.RED : ColorRGB.WHITE; } }
où ColorRGB.RED et ColorRGB.WHITE sont simplement des constantes prédéfinies pour les couleurs (1, 0, 0) et (1, 1, 1), respectivement.
En affichant cette image à l'écran au moyen de l'infrastructure que nous vous fournissons, on obtient bien ce à quoi on s'attend :

Figure 1 : Le cercle rouge unitaire sur fond blanc
A noter que l'on ne représente ci-dessus qu'une portion de l'image complète, puisqu'elle est infinie. Cette portion est comprise entre -2 et +2 pour la coordonnée x, et entre approximativement -1.4 et +1.4 pour la coordonnée y.
Exercice 1
Téléchargez l'archive Zip s02-images.zip, qui contient la définition de l'interface ImageRGB, la classe ColorRGB, la classe RedWhiteUnitCircleGenerator ainsi qu'un programme principal ImageViewer qui affiche une image à l'écran. En l'état, l'image qu'il affiche est celle du cercle ci-dessus.
Prenez un moment pour vous familiariser avec la classe ColorRGB. Jetez aussi vite un œil à la classe ImageViewer afin de trouver l'endroit, signalé par un commentaire, où l'image à afficher est créée. Vous devrez modifier l'expression de création d'image tout au long de cette série.
Vous pouvez également, si vous le désirez, lire en détail le code des classes ImageViewer et ImageComponent, mais d'une part cela n'est pas nécessaire à la suite du mini-projet, et d'autre part elles utilisent des concepts que nous n'avons pas encore vus au cours.
Une fois cela fait, et en vous inspirant de la classe RedWhiteUnitCircleGenerator, écrivez des classes pour représenter chacun des trois types d'images ci-dessous.
Echiquier
La première classe à écrire, nommée p.ex. ChessboardGenerator, doit représenter un échiquier à cellules carrées, dont la taille et les deux couleurs doivent être configurables, c-à-d qu'on doit pouvoir les passer au constructeur de la classe. Une taille de cellule négative ou nulle doit provoquer la levée de l'exception IllegalArgumentException.
Conseil : la méthode floor de la classe java.lang.Math peut être utile.

Figure 2 : Un échiquier noir et blanc aux cases d'une largeur de 0.5
Cible
La seconde classe à écrire, nommée p.ex. BullseyeGenerator, doit décrire une « cible » formée de cercles concentriques. Là aussi, la largeur des bandes doit être configurable, de même que les deux couleurs.
Conseil : la méthode floor de la classe java.lang.Math peut à nouveau être utile.

Figure 3 : Une cible rouge et bleue aux bandes d'une largeur de 0.5
Dégradé linéaire
La troisième classe à écrire, nommée p.ex. LinearHorizontalGradientGenerator, doit produire un dégradé linéaire horizontal entre deux couleurs placées à deux coordonnées x distinctes. Les deux couleurs ainsi que les coordonnées x de l'une et de l'autre doivent être configurables. L'exception IllegalArgumentException doit être levée par le constructeur si la première coordonnée x est supérieure ou égale à la seconde.
Conseil : la méthode mixWith de la classe ColorRGB fournie peut être utile ici.

Figure 4 : Un dégradé linéaire allant du vert (en -1) au bleu (en +1)
Exercice 2
Les implémentation de l'interface ImageRGB du premier exercice peuvent être qualifiées de génératrices, dans la mesure où elles génèrent une image. Mais il est aussi possible de définir des classes transformatrices qui, étant donnée une image existante, en produisent une nouvelle.
Par exemple, on peut facilement définir une classe qui, étant donnée une image, la rétrécit d'un facteur 2 parallèlement à l'axe vertical :
public class ShrinkVerticallyByTwoTransformer implements ImageRGB { private final ImageRGB image; public ShrinkVerticallyByTwoTransformer(ImageRGB image) { this.image = image; } @Override public ColorRGB valueAt(double x, double y) { return image.valueAt(x, y * 2.0); } }
Notez bien dans ce code que la composante y est multipliée par deux pour obtenir un rétrécissement de l'image finale. Comprenez-vous pourquoi ?
En l'appliquant à l'image du cercle rouge unitaire, on obtient :

Figure 5 : Le cercle rouge unitaire écrasé
Le but de ce second exercice est de définir une classe transformatrice, nommée p.ex. RotationTransformer, qui applique une rotation autour de l'origine à une image. L'angle de rotation doit être passé en radians, et un angle positif doit représenter une rotation dans le sens contraire des aiguilles d'une montre.
Conseil : si vous ne vous souvenez plus des formules permettant d'effectuer une rotation dans le plan, consultez la page Wikipedia à ce sujet.
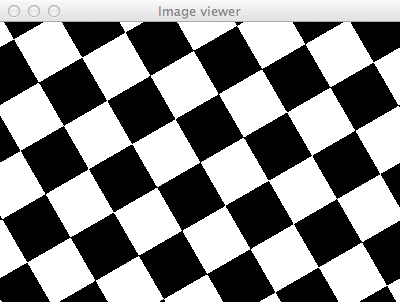
Figure 6 : Un échiquier tourné de 30°
Exercice 3
Comme dit dans l'introduction, notre notion d'images continues et infinies contraste avec la notion habituelle d'image discrète et finie. Il est toutefois possible de passer de l'une à l'autre assez facilement.
Ainsi, la classe ImageComponent que nous vous fournissons convertit les images infinies et continues qu'on lui demande d'afficher en images discrètes, car il est bien entendu impossible d'afficher une image infinie continue à l'écran.
Le but de ce troisième exercice est d'écrire une classe, nommée p.ex. DiscreteImageAdapter, faisant le passage inverse, c-à-d prenant en argument une image discrète et produisant une image infinie. En plus de l'image discrète à convertir, cette classe doit prendre une couleur de fond en argument. Pour tous les points situés en dehors des bornes de l'image discrète, cette classe doit produire la couleur de fond. Pour ceux situés dans les bornes de l'image discrète, elle doit produire la couleur du pixel le plus proche du point donné.
Pour faciliter les choses, l'image discrète doit être redimensionnée et translatée de manière à ce que son centre se trouve à l'origine, et qu'elle ait une largeur de 2 unités. Bien entendu, le redimensionnement doit préserver le rapport largeur/hauteur de l'image.
Pour représenter les images discrètes, utilisez la classe BufferedImage du paquetage java.awt.image. Sa méthode getRGB permet d'obtenir la couleur d'un pixel, dont les trois composantes sont « empaquetées » dans un entier. Cet entier peut directement être passé au second constructeur de notre classe ColorRGB pour obtenir la couleur correspondante.
Pour obtenir une image BufferedImage à partir d'un fichier sur disque ou présent sur le réseau, il convient d'utiliser la classe ImageIO du paquetage javax.imageio, et éventuellement la classe URL du paquetage java.net pour représenter les adresses URL. Par exemple, une image de Dubrovnik peut être obtenue depuis notre serveur et transformée en BufferedImage au moyen des deux lignes suivantes :
URL imageURL = new URL("http://cs108.epfl.ch/images/dubrovnik.jpg"); BufferedImage discreteImage = ImageIO.read(imageURL);
En appliquant votre classe de transformation à cette image de Dubrovnik et une couleur de fond noir, vous devriez obtenir l'image ci-dessous.
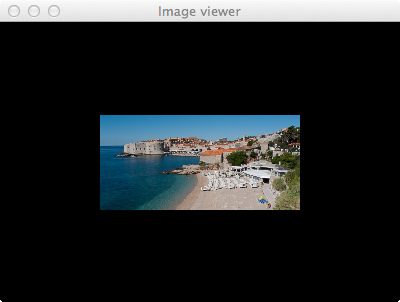
Figure 7 : Une image discrète et finie convertie en image continue et infinie
A noter que la technique consistant à retourner le point le plus proche, nommée nearest neighbor en anglais, est loin d'être idéale et produit des images de relativement mauvaise qualité dès que l'on effectue, par exemple, une rotation ou un redimensionnement. Il existe d'autres méthodes qui produisent de meilleurs résultats, comme l'interpolation bilinéaire, que les personnes qui auraient terminé la série avant la fin de la séance d'exercices mettront en œuvre.