Le projet Isochrone-TL
Le but du projet Isochrone-TL est d'écrire un programme de visualisation de cartes isochrones pour les transports publics de la région lausannoise (tl).
Une carte isochrone permet de visualiser, étant donnés un lieu et une heure de départ, le temps nécessaire pour atteindre n'importe quel point de la carte en utilisant un ou plusieurs moyens de transport déterminés. Pour ce projet, les deux seuls moyens de transport considérés sont la marche à pied et les véhicules des tl, à savoir les bus et métros m1 et m2.
La copie d'écran ci-dessous montre un exemple de carte isochrone pour le 1er octobre 2013 à 6h08 en partant de l'arrêt Lausanne-Flon. A l'arrière plan, on distingue une carte de la région lausannoise — fournie par le projet OpenStreetMap — tandis que l'avant-plan semi-transparent est colorié en fonction du temps de parcours. Ainsi, tous les points accessibles en 5 minutes ou moins depuis l'arrêt Lausanne-Flon, en combinant la marche à pied et les véhicules des tl, sont coloriés en rouge. Ceux accessibles en 5 à 10 minutes sont en orange, ceux accessibles en 10 à 15 minutes en jaune, et ainsi de suite. Finalement, tous ceux accessibles en 45 minutes ou plus sont en noir.
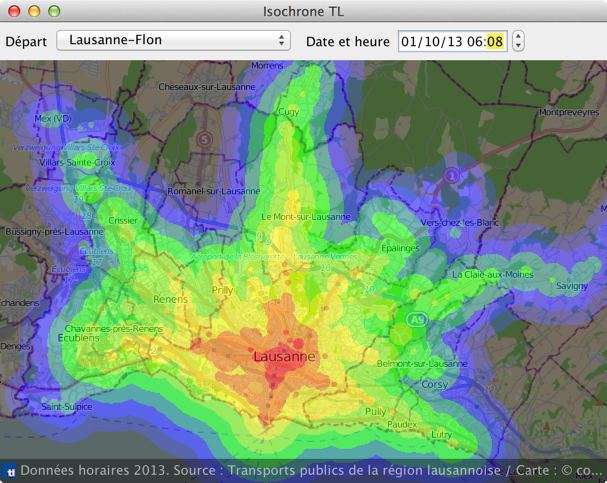
Figure 1 : Une carte isochrone
Il faut noter que cette carte n'est pas rigoureusement exacte, car deux hypothèses simplificatrices ont été faites lors de son dessin :
- On a supposé que le temps nécessaire pour aller à pied d'un point à un autre ne dépend que de la distance séparant ces deux points à vol d'oiseau. Lorsque le réseau routier est dense, comme en région urbaine, cette hypothèse n'est pas mauvaise, son principal défaut étant d'ignorer totalement les obstacles infranchissables à pied, comme les bâtiments, les autoroutes ou les lacs et rivières.
- On a supposé que le temps de changement de véhicule était nul, ce qui permet parfois d'obtenir des liaisons irréalistes en pratique. Ainsi, il arrive parfois qu'un métro m1 arrive à l'arrêt Bourdonnette une minute avant qu'un bus n'en parte, mais en pratique il n'est que rarement possible de passer de l'un à l'autre.
Malgré ces simplifications, propres à ce projet, les cartes isochrones obtenues peuvent être utiles dans un certain nombre de situations. Voici quelques exemples :
- Une personne cherchant un nouveau logement peut utiliser une carte isochrone pour repérer les régions rapidement accessibles depuis son lieu de travail.
- Une entreprise de transports en commun peut utiliser des cartes isochrones pour évaluer la couverture de son offre et détecter les éventuelles régions mal desservies.
- Deux personnes travaillant à des endroits différents et désirant se rencontrer peuvent utiliser deux cartes isochrones pour identifier les endroits rapidement accessibles aux deux.
- Une personne désirant manger en dehors de son lieu de travail à midi peut utiliser une carte isochrone pour identifier les endroits rapidement accessibles.