Examen final : corrigé
1 Fonctions
Cet exercice ressemble passablement au mini-projet images continues, car dans les deux cas l'idée est de représenter des fonctions mathématiques par des objets implémentant une interface donnée. La différence principale est que dans le cas des images les fonctions font correspondre un point à une valeur (souvent une couleur), alors qu'ici elles font correspondre un réel à un réel.
Partie 1
La classe Linear est similaire aux générateurs d'images du mini-projet images continues. Elle est paramétrisée par les valeurs de a et b et sa méthode valueAt est une simple traduction en Java de la formule mathématique de l'énoncé.
public final class Linear implements FunctionRR { private final double a, b; public Linear(double a, double b) { this.a = a; this.b = b; } @Override public double valueAt(double x) { return a * x + b; } }
Partie 2
La classe Derivative est similaire aux transformateurs d'images dans le projet images continues. Là aussi l'idée est de « modifier » une fonction existante, en l'occurence en calculant sa dérivée au moyen de la formule donnée dans l'énoncé.
public final class Derivative implements FunctionRR { private final FunctionRR f; private final double delta; public Derivative(FunctionRR f, double delta) { this.f = f; this.delta = delta; } @Override public double valueAt(double x) { return (f.valueAt(x + delta) - f.valueAt(x - delta)) / (2.0 * delta); } }
Partie 3
La classe Composition est quant à elle similaire aux « composeurs » d'images du mini-projet images continues. Là aussi l'idée est de composer deux fonctions existantes pour en obtenir une nouvelle.
public final class Composition implements FunctionRR { private final FunctionRR f1, f2; public Composition(FunctionRR f1, FunctionRR f2) { this.f1 = f1; this.f2 = f2; } @Override public double valueAt(double x) { return f1.valueAt(f2.valueAt(x)); } }
Partie 4
La classe Derivative utilise bien entendu le patron Decorator tandis que Composition utilise le patron Composite.
2 Fonctions interpolées
Cet exercice avait aussi quelques ressemblances avec certaines parties du projet images continues. En particulier, l'interpolation linéaire d'une fonction entre deux points est une version généralisée du masque dégradé de la série 3.
Partie 1
La classe InterpolatedFunction doit mémoriser les deux tableaux passés à son constructeur et décrivant les points connus. Pour ce faire, elle contient deux champs nommés xs et ys ci-dessous.
public final class InterpolatedFunction implements FunctionRR { private final double[] xs, ys; // ... constructeur et méthodes }
Le constructeur doit commencer par vérifier la validité des tableaux reçus puis en stocker une copie dans ces champs, afin de garantir l'immuabilité de la classe. Pour vérifier que le premier tableau est trié et sans doublon, il suffit de vérifier que chacun de ses éléments est strictement inférieur à son successeur.
public final class InterpolatedFunction implements FunctionRR { private final double[] xs, ys; public InterpolatedFunction(double[] xs, double[] ys) { if (xs.length != ys.length) throw new IllegalArgumentException(); if (xs.length == 0) throw new IllegalArgumentException(); for (int i = 1; i < xs.length; ++i) { if (! (xs[i - 1] < xs[i])) throw new IllegalArgumentException(); } this.xs = Arrays.copyOf(xs, xs.length); this.ys = Arrays.copyOf(ys, ys.length); } // ... méthode valueAt }
Le premier tableau étant trié, la méthode valueAt peut y faire une recherche dichotomique (au moyen de la méthode binarySearch) afin de calculer son résultat. Elle peut ensuite distinguer quatre cas :
- le point reçu fait partie des points connus, auquel cas on retourne son image connue sans faire de calcul,
- le point reçu est inférieur au plus petit point connu, auquel cas on retourne l'image du plus petit point,
- le point reçu est supérieur au plus grand point connu, auquel cas on retourne l'image du plus grand point,
- le point reçu est entre deux points connus, auquel cas on doit interpoler linéairement.
Dans le premier cas, la fonction binarySearch retourne une valeur positive, dans les autres cas elle retourne une valeur négative qu'il convient d'adapter pour obtenir la position d'insertion. Au moyen de cette dernière, il est facile de distinguer les trois derniers cas.
public final class InterpolatedFunction implements FunctionRR { private final double[] xs, ys; // ... constructeur @Override public double valueAt(double x) { int p = Arrays.binarySearch(xs, x); if (p >= 0) return ys[p]; else { int i = -(p + 1); if (i == 0) return ys[0]; else if (i == xs.length) return ys[ys.length - 1]; else { assert 0 < i && i < xs.length; double dx = xs[i] - xs[i - 1]; double dy = ys[i] - ys[i - 1]; return ys[i - 1] + (x - xs[i - 1]) / dx * dy; } } } }
Bien entendu, il est aussi possible de faire une simple recherche linéaire dans le tableau xs plutôt qu'une recherche dichotomique.
Partie 2
Le bâtisseur doit stocker les paires \((x, f(x))\) ajoutés via addPair, et pour ce faire une table associative est un bon choix, pour deux raisons :
- la méthode
putremplace l'éventuelle association existante pour la clef reçue par la nouvelle, ce qui est le comportement demandé, - en utilisant une table associative de type
TreeMap, les éléments sont triés par ordre croissant de clef, ce qui est exactement ce qu'exige le constructeur deInterpolatedFunctionécrit ci-dessus.
Le bâtisseur se contente donc de stocker les paires passées à addPair dans une table associative en utilisant x comme clef et y (c-à-d f(x)) comme valeur. Dans la méthode build, les éléments de cette table associative sont parcourus afin de créer les tableaux à passer au constructeur de InterpolatedFunction, qui est finalement appelé.
public static final class Builder { private Map<Double, Double> points = new TreeMap<>(); public void addPair(double x, double y) { points.put(x, y); } public InterpolatedFunction build() { double[] xs = new double[points.size()]; double[] ys = new double[points.size()]; int i = 0; for (double x: points.keySet()) { xs[i] = x; ys[i] = points.get(x); i++; } return new InterpolatedFunction(xs, ys); } }
Partie 3
On pourrait utiliser le patron Strategy pour paramétrer la classe InterpolatedFunction avec une technique d'interpolation.
3 Tableau et table associative
Partie 1
Le but étant de permettre de voir des éléments d'un premier type (ici « tableau de E ») comme des éléments d'un second type (ici « table associative d'entiers vers E »), il faut utiliser le patron Adapter.
Partie 2
La classe ArrayToMap doit bien entendu être générique pour pouvoir adapter des tableaux de n'importe quel type. A l'exception de iterator, les méthodes s'écrivent en une simple ligne :
public final class ArrayToMap<E> implements Map<Integer, E> { private final E[] array; public ArrayToMap(E[] array) { this.array = array; } @Override public boolean isEmpty() { return size() == 0; } @Override public int size() { return array.length; } @Override public E get(Integer key) { return containsKey(key) ? array[key] : null; } @Override public boolean containsKey(Integer key) { return 0 <= key && key < array.length; } // ... iterator (voir plus bas) }
A première vue, l'itérateur ne paraît pas très difficile à écrire : il suffit qu'il stocke l'index du prochain élément à retourner, qui parcourt le tableau, et le tour est joué. Malheureusement, ce n'est pas aussi simple que cela, étant donné que sa méthode next doit produire des instances d'une classe implémentant l'interface Map.Entry<Integer, E>…
Pour ce faire, le plus simple consiste à retourner, dans la méthode next, une instance d'une classe anonyme implémentant l'interface Map.Entry. Etant donné que l'itérateur lui-même se définit naturellement avec une classe anonyme, on se retrouve avec deux classes anonymes imbriquées, mais cela ne pose pas de problème particulier.
public final class ArrayToMap<E> implements Map<Integer, E> { private final E[] array; // ... autres méthode (voir ci-dessus) @Override public Iterator<Map.Entry<Integer, E>> iterator() { return new Iterator<Map.Entry<Integer,E>>() { int nextIndex = 0; @Override public boolean hasNext() { return nextIndex < array.length; } @Override public Map.Entry<Integer, E> next() { return new Map.Entry<Integer, E>() { private final int key = nextIndex++; @Override public Integer key() { return key; } @Override public E value() { return array[key]; } }; } @Override public void remove() { throw new UnsupportedOperationException(); } }; } }
4 Transformation MTF
Pour décoder un flot encodé au moyen de la transformation move to front, il faut garder une table identique à celle utilisée lors de l'encodage. La classe MTFInputStream possède donc un champ, nommé table ci-dessous, contenant la table de décodage. Cette table est initialisée dans le constructeur de la manière décrite dans l'énoncé, c-à-d que l'octet n est placé à la position n dans la table. Pour représenter la table on peut utiliser un tableau-liste, qui offre les opérations permettant de facilement effectuer les mises à jour requises.
public final class MTFInputStream extends InputStream { private final ArrayList<Integer> table; private final InputStream s; public MTFInputStream(InputStream s) { ArrayList<Integer> initialTable = new ArrayList<>(); for (int i = 0; i <= 0xFF; ++i) initialTable.add(i); this.s = s; this.table = initialTable; } // ... méthodes read et close }
La méthode read de la classe MTFInputStream lit le prochain octet du flot sous-jacent, le décode, met à jour la table puis retourne l'octet décodé. Bien entendu, lorsque le flot sous-jacent est épuisé (c-à-d que sa méthode read retourne -1), le flot décodé l'est également.
La valeur produite par le flot sous-jacent est encodée selon la technique MTF, ce qui implique qu'elle représente l'index, dans la table de décodage (à tout moment égale à celle d'encodage), de l'élément décodé. Ce dernier s'obtient donc simplement au moyen de la méthode get.
La mise à jour de la table consiste à placer l'élément décodé en tête de la table. Pour ce faire, il convient de le retirer (au moyen de la méthode remove) de la table puis de l'insérer (au moyen de la méthode add) en tête. Pour éviter les déplacements inutiles lorsque cet élément est déjà en tête de la table, le code ci-dessous n'effectue pas la suppression/réinsertion dans ce cas, mais cela est optionnel.
La méthode close de MTFInputStream ferme simplement le flot sous-jacent, comme d'habitude.
public final class MTFInputStream extends InputStream { private final ArrayList<Integer> table; private final InputStream s; // ... constructeur @Override public int read() throws IOException { int b = s.read(); if (b == -1) return -1; else { int decodedB = table.get(b); if (b != 0) table.add(0, table.remove(b)); return decodedB; } } @Override public void close() throws IOException { s.close(); } }
5 Systèmes de coordonnées géographiques
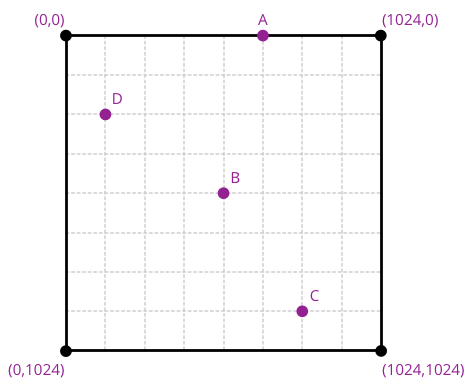
Au niveau de zoom 2, le monde est représenté par un carré de 28+2 = 1024 unités de côté. Le carré étant divisé en 8 parties, chaque carreau quadrillé représente 128 unités. Pour déterminer la position des points A à D, il convient donc dans un premier temps de les convertir dans le système OSM au niveau 2 puis de diviser leurs coordonnées par 128 pour savoir où les placer. On obtient les valeurs suivantes :
| Point | Coordonnées | OSM 2 | OSM 2 / 128 |
|---|---|---|---|
| A | OSM 1 (320,0) | (640, 0) | (5,0) |
| B | WGS 84 (0°,0°) | (512, 512) | (4, 4) |
| C | OSM 4 (3072, 3584) | (768, 896) | (6, 7) |
| D | OSM 2 (128, 256) | (128, 256) | (1, 2) |
Une fois ces calculs effectués, il est trivial de placer les points sur l'image, pour obtenir le résultat ci-dessous.
6 Algorithme de Dijkstra
Partie 1
| No | A | B | C | D | E | F | G | H | Visité |
|---|---|---|---|---|---|---|---|---|---|
| 1 | ∞ | 6h00 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | B |
| 2 | 6h04 | 6h05 | A | ||||||
| 3 | 6h07 | 6h20 | C | ||||||
| 4 | 6h18 | 6h06 | F | ||||||
| 5 | 6h17 | 6h13 | D | ||||||
| 6 | 6h16 | H | |||||||
| 7 | E | ||||||||
| 8 | G |
A noter que le nœud G est inatteignable, donc son heure de première arrivée reste à sa valeur initiale infinie (∞).
Partie 2
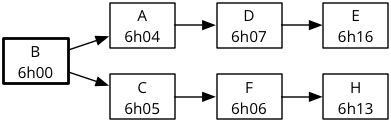
Pour dessiner l'arbre des trajets les plus rapides, il suffit de consulter la table construite ci-dessus. Le prédécesseur d'un nœud est simplement le nœud visité lors de l'itération précédant la dernière mise à jour de l'heure de première arrivée du nœud. Par exemple, l'heure de première arrivée au nœud E a été mise à jour pour la dernière fois à l'itération 6, donc son prédécesseur est le nœud visité lors de l'itération précédente, D.
Le nœud G étant inatteignable, il ne fait pas partie de l'arbre des trajets les plus rapides.
7 Dessin de tuiles isochrones
Partie 1
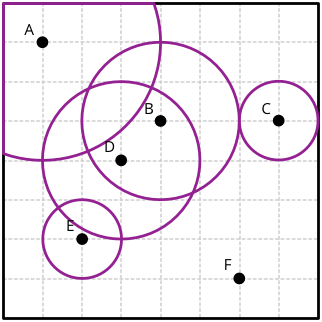
Etant donné que la tuile peut être traversée d'un côté à l'autre en 40 minutes et est découpée en 8, chaque carré quadrillé représente 5 minutes de marche. Le rayon de chaque cercle à dessiner se calcule simplement en soustrayant de 15 minutes le temps nécessaire pour arriver à l'arrêt concerné en partant à 12h05 de l'arrêt A. Par exemple, il faut 10 minutes pour arriver à l'arrêt C, il reste alors 5 minutes de marche, donc le cercle associé à cet arrêt a un rayon de 1 unité.
Partie 2
Non, cette optimisation n'est pas correcte car il est possible que des arrêts soient en dehors d'une tuile mais qu'ils permettent néanmoins d'atteindre, à pied, certains de ses points. Par exemple, si l'arrêt A était déplacé de deux unités sur la gauche, il sortirait de la tuile mais son cercle recouvrirait toujours une partie de celle-ci.