Etape 9 – Tuiles de cartes isochrones
1 Introduction
Cette étape a deux buts :
- écrire le fournisseur de tuiles pour cartes isochrones, et
- écrire un transformateur de fournisseur de tuiles rendant les images des tuiles partiellement tranparentes.
Le transformateur sera utilisé ultérieurement pour rendre les tuiles isochrones partiellement transparentes et permettre ainsi leur composition avec les tuiles OpenStreetMap servant de fond de carte.
1.1 Cartes isochrones
Sur une carte isochrone, chaque point est colorié en fonction du temps nécessaire pour l'atteindre, avec des moyens de transports définis, depuis un lieu de départ et à une date et une heure choisies.
Pour ce projet, les temps nécessaires pour atteindre les différents points de la carte sont groupés en un nombre fini de tranches, et chaque tranche est coloriée avec une couleur différente. Par exemple, on peut imaginer grouper ces temps en 4 tranches de 10 minutes, ayant chacune sa couleur. Dans ce cas, tous les points atteignables en 10 minutes ou moins sont dans la première tranche et coloriés avec la couleur correspondante. Tous les points atteignables en un temps compris entre 10 et 20 minutes sont dans la seconde tranche et coloriés avec la couleur correspondante. Il en va de même pour la troisième tranche, tandis que la quatrième tranche regroupe tous les points qui ne sont pas atteignables en moins de 30 minutes. Ainsi, à chaque point de la carte correspond exactement une tranche et donc une couleur.
Pour dessiner une telle carte, il faut commencer par calculer l'arbre des trajets les plus rapides correspondant aux paramètres choisis — arrêt, date et heure de départ. Cela fait, il reste à déterminer la couleur de chaque point.
Une manière simple mais très peu efficace de déterminer la couleur d'un point consiste à calculer l'heure d'arrivée en ce point puis d'en déterminer la tranche à laquelle il appartient et donc sa couleur. Heureusement, étant données les hypothèses faites pour ce projet, il existe une manière beaucoup plus rapide de procéder.
Pour la comprendre, imaginons dans un premier temps vouloir simplement colorier en rouge tous les points de la carte atteignables en moins de 30 minutes en partant de Lausanne-Flon à 6h08 le 1er octobre 2013. Pour ce faire, on commence par calculer l'arbre des trajets les plus rapides pour ces paramètres. Ensuite, pour chaque arrêt atteignable, on dessine sur la carte un disque rouge centré sur l'arrêt et dont le rayon est la distance faisable à pied dans le temps restant, à savoir 30 minutes moins le temps nécessaire pour atteindre l'arrêt en question.
Par exemple, avec les paramètres donnés ci-dessus, l'arrêt 1er Mai est atteignable à 6h26, donc en 18 minutes. Cela signifie que tous les points atteignables en 30 - 18 = 12 minutes à pied depuis cet arrêt sont atteignables en 30 minutes ou moins depuis Lausanne-Flon. Ces points sont ceux qui se trouvent dans un cercle centré sur l'arrêt 1er Mai et dont le rayon est égal à la distance que l'on peut parcourir à pied en 12 minutes. On peut donc dessiner un disque rouge centré sur l'arrêt 1er Mai et ayant ce rayon. En procédant de la même manière pour tous les arrêts, on colorie effectivement en rouge tous les points atteignables en moins de 30 minutes depuis Lausanne-Flon le 1er octobre 2013 à 6h08.
On peut généraliser cette idée pour obtenir l'algorithme ci-dessous qui colorie au moyen d'une couleur C donnée tous les points atteignables en moins de M minutes, où H associe à un arrêt son heure de première arrivée et P lui associe sa position, tandis que Hd est l'heure de départ.
1: pour chaque arrêt atteignable A : 2: T = M - (H(A) - Hd) 3: si T > 0 : 4: R = distance, sur la carte, faisable à pied en un temps T 5: dessiner un disque centré en P(A), de couleur C et rayon R
Dans cet algorithme, T représente le temps de marche restant à disposition après être arrivé à l'arrêt A. Si ce temps est positif, alors on peut d'un seul coup colorier tous les points atteignables en un temps inférieur ou égal à T depuis l'arrêt A en dessinant un disque dont le rayon est la distance que l'on peut parcourir à pied durant ce temps.
La raison pour laquelle il suffit de dessiner un disque est que d'une part on a admis que seule la distance à vol d'oiseau détermine le temps de marche entre deux points — ni le relief ni les obstacles ne sont pris en compte — et d'autre part la projection de Mercator utilisée ici préserve les formes.
L'algorithme ci-dessus permet de colorier tous les points atteignables en moins de M minutes avec une couleur, et il faut donc encore trouver comment l'utiliser pour dessiner la carte isochrone complète. Or cela est très simple : il suffit de répéter cet algorithme pour chaque tranche de temps, en allant de la dernière à la première. A chaque tranche correspond donc, en quelque sorte, une couche de peinture, et pour peu que ces couches soient appliquées dans le bon ordre, on obtient effectivement la carte isochrone attendue.
Pour illustrer cet algorithme, voyons comment on peut l'utiliser pour dessiner la tuile de coordonnées (1061,724) au niveau de zoom 11 d'une carte isochrone pour un départ de Lausanne-Flon le 1er octobre 2013 à 6h08. Pour situer, la tuile OpenStreetMap ayant ces coordonnées est donnée ci-dessous.
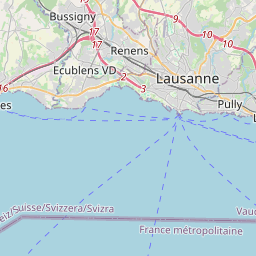
Figure 1 : Tuile OpenSteetMap de coordonnées (1061,724) au niveau de zoom 11
Après avoir calculé l'arbre des trajets les plus rapides correspondant aux paramètres donnés, on peut utiliser l'algorithme ci-dessus pour dessiner les couches successives de la tuile isochrone correspondante. L'animation qui suit illustre le dessin de ces couches. Pour faciliter sa compréhension, le numéro de chaque couche et le nombre de minutes correspondant est affiché dans le coin inférieur gauche.

Figure 2 : Création par couches successives de la tuile isochrone
Il y a un total de 9 couches numérotées de 0 à 8 et coloriées ainsi :
- couche 0 (de fond) : noir, c-à-d le triplet RGB (0,0,0),
- couche 2 : bleu (0,0,1),
- couche 4 : vert (0,1,0),
- couche 6 : jaune (1,1,0),
- couche 8 : rouge (1,0,0).
Les couches intermédiaires (1, 3, 5, 7) sont coloriées avec un mélange des couleurs des couches voisines. Par exemple, la couche 1 est coloriée avec la couleur (0,0,0.5).
Chacune des couches est dessinée au moyen de l'algorithme décrit plus haut, c'est-à-dire en parcourant la totalité des arrêts atteignables et en dessinant pour chacun d'eux un disque dont le rayon représente la distance faisable à pied en le temps restant.
L'animation ci-dessous illustre ce processus pour la couche 3, qui contient tous les points accessibles en 30 minutes ou moins. Pour faciliter sa compréhension, le nom et l'index de l'arrêt sont affichés dans le coin inférieur gauche, et tous les cercles sont d'abord dessinés en rouge avant d'être redessinés dans la bonne couleur. De plus, les arrêts ont été triés du Nord au Sud avant le dessin, ce qui n'est pas nécessaire en pratique.

Figure 3 : Création de la couche 3 par accumulation de cercles
1.2 Encodage des couleurs
Comme nous l'avons vu dans le mini-projet images continues, une couleur peut être représentée par un triplet de trois composantes : la composante rouge, la composante verte et la composante bleue. Chacune de ces trois composantes est un nombre réel compris entre 0 et 1, où 0 représente l'absence de la composante en question, et 1 sa présence maximale. Ainsi, la couleur rouge pur est représentée par le triplet (1,0,0). Ces composantes sont fréquemment appelées canaux (channels en anglais).
Il est parfois utile de représenter des couleurs partiellement transparentes, qui peuvent être mélangées avec d'autres couleurs pour obtenir une couleur finale. Pour ce faire, on ajoute généralement une quatrième composante à une couleur, que l'on appelle le canal alpha (alpha channel). Cette composante est également une valeur réelle comprise entre 0 et 1, où 0 représente une couleur parfaitement transparente (donc invisible) tandis que 1 représente une couleur totalement opaque.
En informatique, ces quatre composantes pourraient être représentées par un quadruplet de valeurs à virgule flottante, p.ex. quatre champs de type double stockés dans un objet. Toutefois, cette représentation est très gourmande en mémoire, raison pour laquelle différentes représentations plus compactes sont généralement utilisées. La plus fréquente d'entre elles consiste à représenter chaque composante par un entier compris entre 0 et 255 (inclus), qui occupe donc exactement 8 bits, et à empaqueter les composantes dans une seule valeur de 32 bits, selon un schéma similaire à celui utilisé dans l'étape 4 pour les trajets.
Ce type de représentation est généralement nommé en énumérant les premières lettres des composantes, dans l'ordre dans lequel elles apparaissent dans la valeur de 32 bits. Par exemple, la représentation ARGB consiste à stocker les quatre composantes en plaçant l'opacité A dans les 8 bits de poids fort, suivi par la composante rouge R, la verte G et finalement la bleue B. Pour passer d'une couleur représentée par un quadruplet de valeurs réelles \((r,g,b,a)\) à une valeur entière de 32 bits au format ARGB désignée par \(p_{ARGB}\), on utilise donc les formules suivantes :
où \(\lVert x\rVert\) représente l'entier le plus proche de \(x\), c-à-d la valeur arrondie de \(x\). Notez bien que la première de ces formules perd de l'information, puisque le nombre potentiellement infini de valeurs possibles pour chaque composante est réduit à 256 valeurs différentes. Cette représentation d'une valeur continue par un petit ensemble de valeurs discrètes est nommée quantification en théorie du signal.
Les couleurs ainsi encodées sont facilement interprétables lorsqu'elles sont représentées sous forme hexadécimale — c-à-d en base 16 — car chacune des composantes occupe alors exactement deux chiffres hexadécimaux. Par exemple, la valeur FF0080EE16 est la représentation encodée d'une couleur dont :
- la composante
Avaut FF16 (c-à-d 25510, donc 1), - la composante
Rvaut 0016 (c-à-d 0), - la composante
Gvaut 8016 (c-à-d 12810, donc environ 0.502), et - la composante
Bvaut EE16 (c-à-d 23810, donc environ 0.933).
2 Mise en œuvre Java
Le fournisseur de tuiles isochrones est défini par la classe IsochroneTileProvider. Une classe séparée, ColorTable, est définie pour représenter la table des couleurs à utiliser pour colorier la carte.
Le transformateur de fournisseur abstrait est quant à lui défini par la classe abstraite FilteringTileProvider. Le transformateur qui rend les tuiles partiellement transparentes est défini dans une sous-classe concrète de ce transformateur abstrait, nommée TransparentTileProvider.
2.1 Classe ColorTable
La classe ColorTable du paquetage ch.epfl.isochrone.tiledmap, publique et finale, modélise une table de couleurs à utiliser pour dessiner une carte isochrone. Elle est paramétrisée par la durée (en secondes) des tranches et par une liste de couleurs, qui doit contenir au moins un élément.
La première couleur est utilisée pour colorier les points appartenant à la première tranche, c-à-d ceux atteignables en un temps inférieur à la durée des tranches. La seconde couleur est utilisée pour colorier les points appartenant à la seconde tranche, c-à-d ceux atteignables en un temps supérieur à la durée des tranche mais inférieur ou égal à deux fois la durée des tranches. Et ainsi de suite jusqu'à la dernière couleur, qui est utilisée pour colorier tous les points n'ayant pas encore de couleur.
Cette classe possède des méthodes permettant d'obtenir la durée de chaque tranche, le nombre de tranches, ainsi que la couleur associée à une tranche.
Les couleurs sont représentées par la classe Color du paquetage java.awt, qui ressemble à la classe Color du mini-projet images continues.
2.2 Classe IsochroneTileProvider
La classe IsochroneTileProvider du paquetage ch.epfl.isochrone.tiledmap, publique et finale, est un fournisseur de tuiles pour carte isochrone. Elle est paramétrisée par un arbre des trajets les plus rapides, une table de couleur et une vitesse de marche à pied. Cette dernière est nécessaire au calcul du rayon des disques à dessiner.
Pour dessiner l'image de la tuile, il faut commencer par créer une image de type BufferedImage, puis créer un contexte graphique qui lui soit associé et finalement utiliser des méthodes de dessin sur ce dernier. Le contexte graphique est un objet contenant les informations liées au dessin, p.ex. la couleur à utiliser pour dessiner. En Java, ce contexte est représenté par la classe Graphics2D du paquetage java.awt.
L'extrait de programme ci-dessous illustre la création d'une image au moyen des méthodes de dessin fournies par le contexte graphique. Il crée une image carrée de 100 pixels de côté, obtient son contexte graphique, remplit l'image avec un fond blanc puis dessine un disque inscrit dans un carré de 125 pixels de côté dont le coin haut-gauche est en (-50, -50), avant d'écrire l'image dans un fichier au format PNG.
BufferedImage i = new BufferedImage(100, 100, BufferedImage.TYPE_INT_ARGB); Graphics2D g = i.createGraphics(); // Remplit avec un fond blanc g.setColor(Color.WHITE); g.fillRect(0, 0, i.getWidth(), i.getHeight()); // Dessine le cercle g.setColor(Color.RED); g.fill(new Ellipse2D.Double(-50, -50, 125, 125)); // Ecrit l'image dans un fichier ImageIO.write(i, "png", new File("image.png"));
L'image produite par cet extrait de programme apparaît ci-dessous. Pour plus de détails sur les méthodes utilisées, reportez-vous à la documentation des classes Graphics2D et Ellipse2D.

Figure 4 : Un cercle rouge sur fond blanc
2.3 Classe FilteringTileProvider
La classe FilteringTileProvider du paquetage ch.epfl.isochrone.tiledmap, publique et abstraite, représente un transformateur de fournisseur de tuiles qui transforme l'image des tuiles de son fournisseur sous-jacent, pixel par pixel.
La transformation de la couleur d'un pixel individuel est effectuée par la méthode abstraite transformARGB qui reçoit en argument la couleur d'un pixel au format ARGB et retourne la couleur transformée de ce pixel. Cette méthode a le profil suivant :
abstract public int transformARGB(int argb);
2.4 Classe TransparentTileProvider
La classe TransparentTileProvider du paquetage ch.epfl.isochrone.tiledmap, publique et finale, est un transformateur de fournisseur concret qui hérite de FilteringTileProvider. Ce transformateur est paramétré par une opacité, comprise dans l'intervalle [0;1], qui est l'opacité des tuiles après transformation.
La méthode transformARGB de cette classe ne fait rien d'autre que de remplacer la composante A (alpha) de la couleur reçue en argument par celle spécifiée lors de la construction, sans toucher les autres composantes.
(A noter que l'opacité des tuiles sous-jacentes est totalement ignorée par cette méthode. Il aurait été plus correct de multiplier cette opacité par celle fournie au constructeur de TransparentTileProvider, mais on fait ici l'hypothèse qu'elle vaut toujours 1).
2.5 Test
Pour tester vos différents fournisseurs de tuile, vous pouvez définir un programme très simple les utilisant pour obtenir une tuile puis écrivant l'image de cette tuile dans un fichier. Cela se fait très simplement au moyen de la méthode write de la classe ImageIO comme l'illustre l'extrait de programme ci-dessous qui écrit l'image de la tuile t dans un fichier nommé image.png, au format PNG.
import java.io.File; import javax.imageio.ImageIO; Tile t = …; ImageIO.write(t.image(), "png", new File("image.png"));
3 Résumé
Pour cette étape, vous devez :
- Ecrire les classes
ColorTable,IsochroneTileProvider,FilteringTileProvideretTransparentTileProviderselon les spécifications ci-dessus. - Tester, autant que possible, les classes que vous avez écrites. La manière la plus simple de procéder consiste à produire des fichiers image de vos tuiles comme décrit ci-dessus et à les comparer avec les tuiles données en exemple plus haut.
- Documenter la totalité des entités publiques que vous avez définies.