Etape 7 – Recherche d'horaire
1 Introduction
Le but principal de cette étape — la dernière à faire partie du rendu intermédiaire — est d'écrire la méthode de recherche des plus courts trajets dans le graphe d'horaires, ainsi qu'un petit programme permettant de l'utiliser.
1.1 Recherche des plus courts trajets
La recherche des plus courts trajets dans un graphe d'horaires est très similaire à un célèbre problème de la théorie des graphes, la recherche des plus courts chemins dans un graphe. La seule différence entre les deux problèmes est que, dans un graphe d'horaires, le temps nécessaire au parcours d'un arc donné dépend de l'heure à laquelle on se trouve à son sommet de départ, ce qui n'est pas le cas dans la formulation classique du problème des plus courts chemins. Toutefois, il est facile de prendre en compte cette différence et d'adapter un algorithme de recherche des plus courts chemins classique au cas d'un graphe d'horaire. C'est ce que nous allons faire avec l'un des grands classiques de l'algorithmique, l'algorithme de Dijkstra.
1.2 Algorithme de Dijkstra
L'algorithme de Dijkstra — nommé d'après son inventeur, l'informaticien néerlandais Edsger Dijkstra — permet de trouver les plus courts chemins dans un graphe entre un nœud de départ et tous les autres nœuds du graphe. Seule la variante adaptée aux graphes d'horaires est détaillée ci-dessous, et les personnes intéressées par sa version standard se reporteront à la page Wikipedia (en anglais ou en français) ou aux nombreuses ressources disponibles en ligne pour obtenir plus de détails.
Adapté aux graphes d'horaires, l'algorithme de Dijkstra calcule la première heure d'arrivée possible à tous les arrêts du réseau, étant donnés un arrêt et une heure de départ. Pour ce faire, il tient à jour deux informations : d'une part, une collection des arrêts à visiter, qui sont les arrêts pour lesquels une heure de première arrivée n'est pas encore déterminée avec certitude ; et d'autre part, pour chaque arrêt (visité ou non), la plus petite heure d'arrivée connue à ce stade de l'algorithme.
Initialement, tous les arrêts du réseau font partie de la collection des arrêts à visiter, y compris l'arrêt de départ. De plus, la meilleure heure d'arrivée connue est infinie pour tous les arrêts du réseau sauf l'arrêt de départ, pour lequel elle est égale à l'heure de départ.
Ensuite, l'algorithme itère jusqu'à ce que la collection des arrêts à visiter soit vide. A chaque itération, il visite l'arrêt pas encore visité dont la meilleure heure d'arrivée connue est la plus petite.
Lorsqu'un arrêt est visité, sa meilleure heure d'arrivée connue devient définitive, dans le sens où il est garanti qu'il ne sera pas possible d'y arriver avant cette heure-là. De plus, tous les voisins de l'arrêt visité (c-à-d ceux auxquels il est relié par un arc) sont examinés afin de savoir s'il est possible d'améliorer leur meilleure heure d'arrivée en s'y rendant depuis l'arrêt actuellement visité. La meilleure heure d'arrivée de tous les voisins pour lesquels c'est le cas est mise à jour.
Cet algorithme est résumé ci-dessous sous la forme de pseudo-code où Ad est l'arrêt de départ, Hd l'heure de départ, V la collection des arrêts à visiter et H associe à un arrêt sa meilleure heure d'arrivée connue.
1: V = { tous les arrêts du graphe } 2: H(Ad) = Hd 3: H(x) = ∞ pour tout arrêt x ≠ Ad 4: 5: tant que V n'est pas vide : 6: A = élément x de V tel que H(x) est minimum 7: V = V \ { A } 8: 9: si H(A) = ∞ : 10: stop 11: 12: pour chaque voisin A' de A : 13: H' = heure de première arrivée en A' en partant de A à H(A) 14: si H' < H(A') : 15: H(A') = H'
A noter qu'il est aussi valide de n'examiner que les voisins pas encore visités d'un arrêt, plutôt que de visiter chacun d'entre-eux comme le fait la boucle de la ligne 12. En effet, une propriété fondamentale de l'algorithme de Dijkstra est que l'heure de première arrivée de tous les arrêts visités est garantie minimale, donc le test de la ligne 14 n'est jamais vrai pour les voisins déjà visités.
1.3 Exemple d'exécution
Pour illustrer le fonctionnement de l'algorithme de recherche de plus courts trajets, on peut l'appliquer au graphe d'horaire de la figure 3 de l'énoncé de l'étape 4. Sur les figures ci-dessous, les arrêts visités sont mis en évidence en violet, et la meilleure heure d'arrivée connue pour un arrêt figure à ses côtés.
Initialement, aucun arrêt n'est visité et toutes les heures d'arrivée sont infinies, sauf celle de l'arrêt Bel-Air, puisque c'est là que commence la recherche, à 9h18.
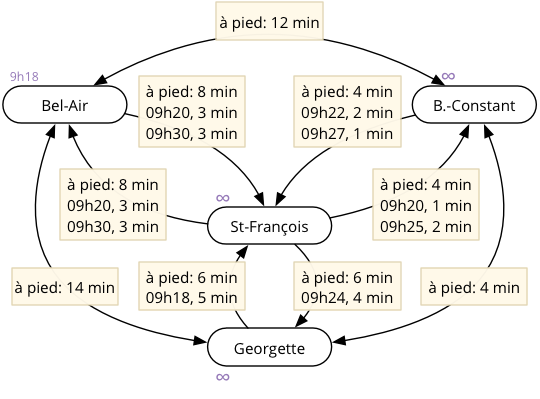
Figure 1 : Etat initial de la recherche
L'arrêt Bel-Air étant l'arrêt non visité avec la plus petite heure d'arrivée, c'est lui que l'algorithme visite pour commencer.
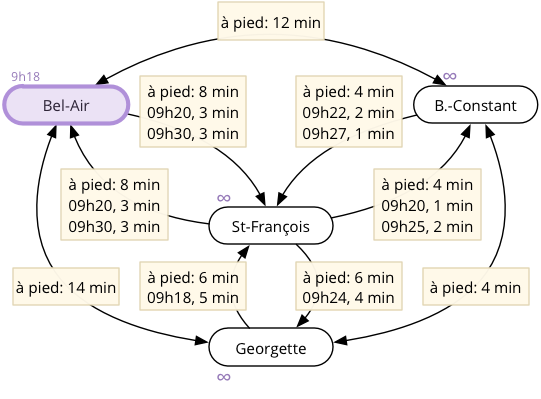
Figure 2 : Visite de l'arrêt Bel-Air
Lors de la visite de l'arrêt Bel-Air, tous ses voisins sont examinés et leur heure d'arrivée est mise à jour s'il est possible de les atteindre plus rapidement depuis Bel-Air. Ici, comme les trois voisins de Bel-Air ont à ce stade une heure d'arrivée infinie, ils sont tous atteignables plus rapidement depuis Bel-Air, et leur heure d'arrivée est donc mise à jour.
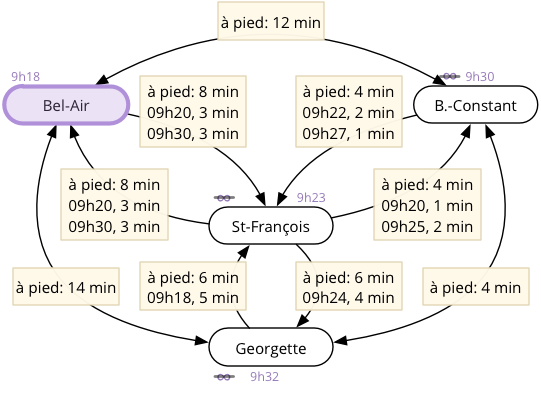
Figure 3 : Mise à jour des heures d'arrivée des voisins de Bel-Air
Une fois la mise à jour des heures d'arrivée des voisins de Bel-Air terminée, l'arrêt non visité ayant la plus petite heure d'arrivée est St-François. C'est donc lui qui est visité ensuite.
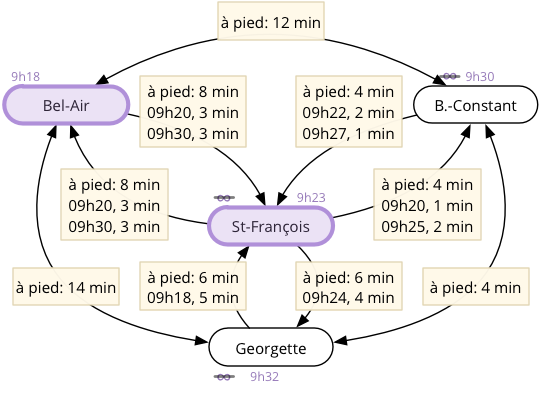
Figure 4 : Visite de l'arrêt St-François
Les voisins de St-François sont examinés et deux d'entre-eux, à savoir B.-Constant et Georgette sont atteignables plus rapidement depuis St-François. Leur heure d'arrivée est donc mise à jour.
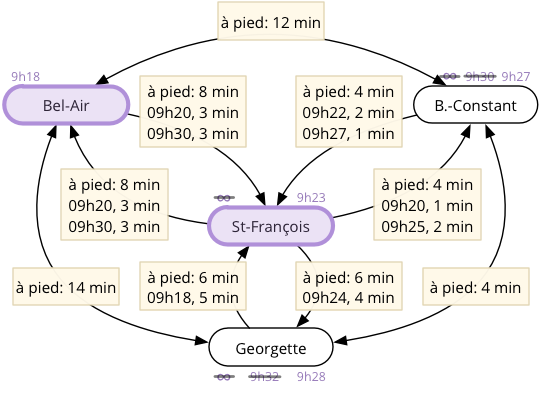
Figure 5 : Mise à jour des heures d'arrivée des voisins de St-François
Le prochain arrêt non visité ayant la plus petite heure d'arrivée est maintenant B.-Constant. C'est donc lui qui est visité. Sa visite ne provoque toutefois pas de mise à jour d'une quelconque heure d'arrivée, car aucun de ses voisins n'est atteignable plus rapidement à travers lui.
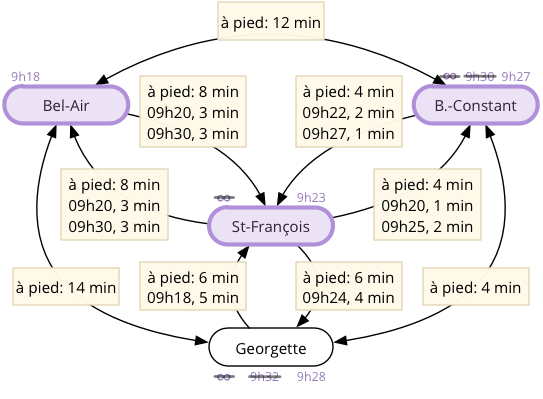
Figure 6 : Visite de l'arrêt B.-Constant
Finalement, le dernier arrêt visité est Georgette. Tous ses voisins ayant été visités, aucune mise à jour de leur heure d'arrivée ne se produit non plus.
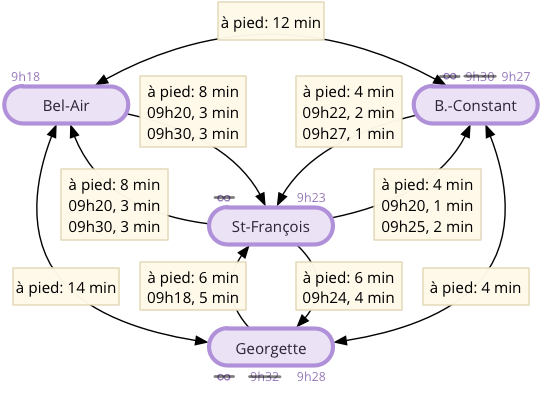
Figure 7 : Visite de l'arrêt Georgette
Tous les arrêts ont maintenant été visités, et l'algorithme termine donc. On peut voir que les heures de première arrivée à chaque arrêt correspondent bien à celles données dans l'arbre de la figure 1 de l'énoncé de l'étape 5. De plus, on constate qu'en se souvenant simplement, lors de la mise à jour d'une heure d'arrivée, du voisin qui a provoqué cette mise à jour, on obtient les arcs de l'arbre des trajets les plus rapides.
Par exemple, l'heure d'arrivée de l'arrêt B.-Constant a été mise à jour la dernière fois lors de la visite de l'arrêt St-François. Dès lors, l'arrêt St-François est le prédécesseur de l'arrêt B.-Constant dans l'arbre des trajets les plus rapides.
2 Mise en œuvre Java
La mise en œuvre Java de la recherche des plus courts trajets se fait dans une unique méthode à ajouter à la classe Graph commencée à l'étape 5.
2.1 Classe Graph
Interface publique
En plus des méthodes décrites à l'étape 5, la classe Graph possède la méthode publique suivante :
FastestPathTree fastestPaths(Stop startingStop, int departureTime), qui retourne l'arbre des trajets les plus rapides pour l'arrêt et l'heure de départ donnés. Lève l'exceptionIllegalArgumentExceptionsi l'arrêt donné ne fait pas partie du graphe ou si l'heure de départ est inférieure à zéro.
Conseils de programmation
La méthode fastestPath n'est pas très longue ni difficile à écrire pour peu que l'on utilise judicieusement les classes écrites lors des étapes précédentes. Il faut noter en particulier que le bâtisseur de FastestPathTree convient très bien pour stocker les meilleures heures d'arrivées connues pour les arrêts, d'autant plus que sa méthode arrivalTime retourne une heure infinie pour tous les arrêts pour lesquels une heure spécifique n'a pas été donnée.
Une partie centrale de l'algorithme de Dijkstra est celle recherchant le prochain arrêt à visiter, qui est celui dont l'heure d'arrivée est la plus petite (ligne 6). Cette recherche peut bien entendu se faire en parcourant tous les éléments de la collection des arrêts à visiter. Il est toutefois possible de faire mieux, au moyen d'une collection que l'on nomme queue de priorité (ou file de priorité).
Une queue de priorité est une queue d'éléments comparables entre-eux, et qui permet un accès rapide au plus petit (ou au plus grand, en fonction des mises en œuvre) élément. Ainsi, si une queue de priorité est utilisée pour stocker les arrêts à visiter, l'obtention du prochain arrêt à visiter peut se faire avec une complexité de \(O(\log n)\), meilleure que la complexité de la recherche linéaire, qui est en \(O(n)\).
Les personnes qui le désirent peuvent essayer d'utiliser une queue de priorité pour stocker les arrêts à visiter, en les comparant par heure d'arrivée. La bibliothèque Java fournit la classe PriorityQueue représentant les queues de priorité, dont la méthode remove permet d'obtenir (et de supprimer de la queue) le plus petit élément de la queue.
Pour dire comment les éléments de la queue doivent être comparés entre-eux, il faut passer au constructeur de PriorityQueue un comparateur, qui est un objet implémentant l'interface java.util.Comparator. Cette interface, à ne pas confondre avec l'interface Comparable, possède une méthode compare permettant de comparer deux objets selon un ordre. L'ordre à utiliser ici est celui des heures de première arrivée, et il faut donc trouver un moyen pour créer un comparateur l'utilisant pour comparer deux arrêts.
Une fois cela fait, il faut prendre garde à un détail capital : la classe PriorityQueue fait l'hypothèse que l'ordre des éléments qu'elle contient ne change pas. Or l'algorithme de Dijkstra peut justement changer l'heure de première arrivée des arrêts (à la ligne 15). Lorsque cela se produit, il faut impérativement supprimer puis réinsérer dans la queue de priorité l'arrêt dont l'heure d'arrivée a été changée, faute de quoi la queue ne se comporte pas correctement !
2.2 Classe TimeTableSearch
La classe Graph terminée, tout est maintenant en place pour faire des recherches d'horaires. Dans ce but, vous devez écrire un programme très simple permettant de rechercher les plus courts trajets entre un arrêt de départ et tous les autres arrêts du réseau des tl, à une date et une heure de départ donnée.
La classe principale de ce programme (c-à-d celle contenant la méthode main) se nomme TimeTableSearch et se trouve dans le paquetage ch.epfl.isochrone. Elle accepte, via le tableau passé à sa méthode main, les paramètres suivants, dans l'ordre :
- le nom de l'arrêt de départ,
- la date de départ, composée de trois nombres séparés par un tiret (
-) et qui représentent respectivement l'année, le mois et le jour (p.ex.2013-10-1pour le 1er octobre 2013), - l'heure de départ, composée de trois nombres séparés par un double point (
:) et représentant respectivement l'heure, les minutes et les secondes de l'heure de départ (p.ex.6:8:0pour 6h08 précises).
Il n'est pas nécessaire de valider ces arguments ni d'afficher un quelconque message d'erreur en cas d'absence ou d'invalidité de l'un d'entre-eux, car ce programme n'a d'autre but que de pouvoir interagir avec le système avant le rendu final. Le programme peut donc simplement terminer avec une exception si le bon nombre d'arguments n'est pas passé, ou s'ils sont invalides.
La recherche se fait sur le réseau des tl, avec les données complètes. Le graphe doit contenir des arcs de trajet à pied entre toutes les paires d'arrêts qu'il est possible de rejoindre en 5 minutes ou moins en marchant à 1.25 m/s. Pour chaque arrêt du réseau atteignable en un temps fini, le programme affiche son nom, l'heure de première arrivée et le chemin pour y arriver.
Par exemple, lancé sur le graphe d'horaire de la figure 3 de l'énoncé de l'étape 4 avec un départ de Bel-Air à 9h18, ce programme devrait afficher le résultat suivant :
B.-Constant : 09:27:00 via: [Bel-Air, St-François, B.-Constant] Bel-Air : 09:18:00 via: [Bel-Air] Georgette : 09:28:00 via: [Bel-Air, St-François, Georgette] St-François : 09:23:00 via: [Bel-Air, St-François]
Lancé sur le graphe d'horaire des tl, avec un départ à 6h08 le 1er octobre 2013 de Lausanne-Flon, ce programme produit un résultat qui débute ainsi (les très longues lignes ont été découpées afin de faciliter la lecture) :
1er Août : 06:27:48
via: [Lausanne-Flon, Port-Franc, EPSIC, Ecole des Métiers,
Couchirard, Prélaz-les-Roses, Galicien, Perrelet,
Renens-Village, Sous l'Eglise, Hôtel-de-Ville, Avenir,
1er Août]
1er Mai : 06:26:00
via: [Lausanne-Flon, Port-Franc, EPSIC, Ecole des Métiers,
Couchirard, Prélaz-les-Roses, Galicien, Perrelet,
Florissant, Broye, Bourg-Dessus, Follieu, Borjod,
Saugiaz, 1er Mai]
Abeilles : 06:23:44
via: [Lausanne-Flon, Rôtillon, Bessières, Ours, CHUV, Sallaz,
Fourmi, Abeilles]
Allières : 06:20:16
via: [Lausanne-Flon, Rôtillon, Bessières, Ours, Béthusy,
Allières]
Alpes : 06:16:00
via: [Lausanne-Flon, Rôtillon, St-François, Georgette, Alpes]
Ancienne Poste : 06:32:00
via: [Lausanne-Flon, Rôtillon, Bessières, Ours, CHUV, Sallaz,
Valmont, Foyer, Rovéréaz, Montblesson, Trois Chasseurs,
Monts-de-Pully, Ravessoud, Claie-Moines, Publoz,
Ancienne Poste]
Arc-en-Ciel : 06:34:00
via: [Lausanne-Flon, Port-Franc, EPSIC, Ecole des Métiers,
Couchirard, Prélaz-les-Roses, Galicien, Perrelet,
Renens-Village, Sous l'Eglise, Hôtel-de-Ville, Avenir,
Renens-14 Avril, Jura, Zinguerie, Arc-en-Ciel]
Aubépines : 06:16:00
via: [Lausanne-Flon, Bel-Air, Chauderon, Ecole Commerce,
Aubépines]
Avenir : 06:25:00
via: [Lausanne-Flon, Port-Franc, EPSIC, Ecole des Métiers,
Couchirard, Prélaz-les-Roses, Galicien, Perrelet,
Renens-Village, Sous l'Eglise, Hôtel-de-Ville, Avenir]
Avenue William : 06:34:00
via: [Lausanne-Flon, Rôtillon, St-François, Georgette,
Eglantine, Avenue du Léman, Bonne-Espérance,
Perraudettaz, Montillier, Pully-Clergère, Reymondin,
Moulins, Paudex, Marronnier, Grand-Pont, Voisinand,
Taillepied, Orzens, Avenue William]
Avenue du Léman : 06:15:00
via: [Lausanne-Flon, Rôtillon, St-François, Georgette,
Eglantine, Avenue du Léman]
Balances : 06:50:00
via: [Lausanne-Flon, Rôtillon, Bessières, Ours, CHUV, Sallaz,
Fourmi, Vennes, Croisettes, Planches, Pré-d'Yverdon,
Perronnaz, Haute-Combe, Chalet à Matthey, Molliettes,
Vers-chez-les-Blanc, Chevreuils, Praz-Collet,
Chalet-à-Gobet, Chalet-Fontaine, Ste-Catherine,
Riau-Graubon, Balances]
Ballègue : 06:32:00
via: [Lausanne-Flon, Rôtillon, Bessières, Ours, CHUV, Sallaz,
Fourmi, Vennes, Croisettes, Planches, Croix Blanche,
Epalinges-Centre, En Praz Bin, Biolleyre, Polny, Ballègue]
Barre : 06:12:59
via: [Lausanne-Flon, Rôtillon, Bessières, Place du Nord, Barre]
Bassenges : 06:24:00
via: [Lausanne-Flon, Vigie, Montelly, Provence, Malley,
Bourdonnette, UNIL-Dorigny, UNIL-Mouline, UNIL-Sorge,
EPFL, Bassenges]
Batelière : 06:16:00
via: [Lausanne-Flon, Lausanne-Gare, Grancy, Délices, Beauregard,
Cèdres, Riant-Cour, Batelière]
Baumettes : 06:23:00
via: [Lausanne-Flon, Port-Franc, EPSIC, Ecole des Métiers,
Couchirard, Prélaz-les-Roses, Galicien, Perrelet,
Florissant, Broye, Bourg-Dessus, Bugnon, Sur-la-Croix,
Baumettes]
Beau-Rivage : 06:16:00
via: [Lausanne-Flon, Lausanne-Gare, Grancy, Délices, Jordils,
Ouchy, Beau-Rivage]
Beau-Site : 06:22:12
via: [Lausanne-Flon, Rôtillon, Bessières, Place du Nord, Tunnel,
Mémise, Grande-Borde, Vieux-Moulin, Casernes,
Stade Olympique, Parc Vélodrome, Beau-Site]
Beaulieu : 06:17:58
via: [Lausanne-Flon, Bel-Air, Chauderon, Ecole Commerce,
Beaulieu]
…
Interface publique
La classe TimeTableSearch étant un programme, elle doit comporter une méthode publique statique nommée main et prenant en argument un tableau de chaînes de caractères contenant les arguments du programme.
Conseils de programmation
Si vous ne vous souvenez plus de comment écrire un programme acceptant des arguments via sa méthode main, reportez-vous à la leçon 10 du cours du semestre d'automne (pp. 41 et suivantes).
Pour découper les chaînes de caractères passées en arguments et représentant les heures et les dates, utilisez bien entendu la méthode split de la classe String. Une fois ces composantes obtenues, convertissez-les en entiers au moyen de la méthode parseInt de la classe Integer.
Pour passer des arguments à un programme depuis Eclipse, il faut cliquer sur l'entrée Run Configurations… du menu Run, puis ouvrir l'onglet nommé Arguments. Tout ce qui est entré dans la zone intitulée Program arguments est passé au programme. Ainsi, pour exécuter le programme TimeTableSearch avec les paramètres mentionnés plus haut, il faut entrer le texte suivant dans cette zone :
Lausanne-Flon 2013-10-01 06:08:00
2.3 Classe Date
Pour terminer cette étape, modifiez votre classe Date pour lui faire implémenter l'interface Comparable. Cela n'avait pas été fait lors de l'étape 2 car vous ne connaissiez pas encore la généricité à ce moment.
3 Résumé
Pour cette étape, vous devez :
- Ecrire la méthode
fastestPathde la classeGraphen fonction des spécifications ci-dessus. - Ecrire le programme
TimeTableSearchen fonction des spécifications ci-dessus. - Rendre votre classe des dates comparables en lui faisant implémenter l'interface
Comparable<Date>. - Compléter la classe de test de la classe
Graphpour tester la nouvelle méthode. - Documenter la totalité des entités publiques que vous avez définies, à l'exception de la classe
TimeTableSearchdont la documentation est optionnelle.