Série 3 – Ensembles par arbres de recherche

Cette série est la troisième du micro-projet consacré aux collections. Comme pour les séries précédentes vous placerez tout votre code dans le paquetage ch.epfl.collections.

Le but de cette série est de compléter votre bibliothèque de collections en y ajoutant une classe Set générique, tout comme vous l'avez fait avec la classe List la semaine dernière. Vous aborderez la constructions de la classe Set générique (et itérable) en plusieurs étapes, détaillées ci-dessous.

Comme d'habitude, nous vous fournissons une version commentée de la définition de l'interface, ici Set, dans le fichier Set.java.

Ensembles d'entiers

Implémentez une classe IntTreeSet qui mette en œuvre l'interface Set<Integer> au moyen d'un arbre de recherche. Pour vous faciliter la tâche, nous mettons à votre disposition un squelette de la classe IntTreeSet dont vous devez implémenter les deux classe internes Node et Leaf.

Une fois votre classe terminée, écrivez, en vous aidant de la bibliothèque JUnit, un test unitaire pour voir si elle semble fonctionner correctement. Un squelette de test vous est fourni.

Ensembles génériques

Rendez votre classe IntTreeSet générique afin qu'elle puisse stocker des éléments d'un type quelconque. Aidez-vous en consultant la documentation de l'interface standard Java Comparable.

Ensembles itérables

Mettez à jour votre interface Set de façon à ce qu'elle implémente l'interface Iterable. Cela permettra aux utilisateurs de votre classe de parcourir les éléments de l'ensemble au moyen de la boucle for-each de Java.

Implémentez ensuite la méthode iterator dans votre classe TreeSet. Comme cela est loin d'être trivial, nous vous suggérons deux solutions : une première relativement simple et inefficace, une seconde plus complexe mais plus efficace.

A noter que dans les deux cas nous ne vous demandons pas de fournir une méthode remove qui fonctionne. Celle-ci doit se contenter de lever l'exception UnsupportedOperationException. La méthode next doit par contre se comporter comme attendu et lever l'exception NoSuchElementException si on l'appelle alors que tous les éléments de l'ensemble ont été parcourus.

Itération via une liste

La solution la plus simple pour écrire la méthode iterator consiste à transformer l'ensemble en une liste puis à itérer sur cette liste. La transformation de l'ensemble en liste nécessite bien entendu l'ajout de méthodes dans l'interface Tree et les deux classes qui l'implémentent.

Itération directe

La seconde solution consiste à stocker une pile de nœuds dans l'itérateur, selon une technique détaillée plus bas.

Une pile est une collection très similaire à une liste, mais dans laquelle on ajoute et supprime les éléments toujours à la même extrémité. Cela se fait au moyen de deux opérations communément appelées push, qui place un nouvel élément sur la pile, et pop, qui supprime et retourne le dernier élément ajouté. Pour plus de détails, vous pouvez consulter l'article Wikipedia au sujet des piles.

Dans l'API Java, la classe LinkedList possède, en plus des méthodes de l'interface List que vous connaissez déjà, des méthode push et pop qui permettent de l'utiliser comme une pile. C'est la collection que nous vous conseillons d'utiliser ici.

La pile à utiliser pour cet itérateur contient à chaque instant les nœuds de l'arbre dont le sous-arbre gauche est en cours de parcours, mais dont le sous-arbre droit n'as pas encore été visité. Initialement, cette pile contient donc l'arête gauche de l'arbre. A chaque itération (c-à-d à chaque appel de la méthode next), le prochain nœud est dépilé, l'arête gauche de son sous-arbre droit est empilée, puis la valeur du nœud est retournée.

Cette technique peut être illustrée sur l'arbre de recherche ci-dessous :

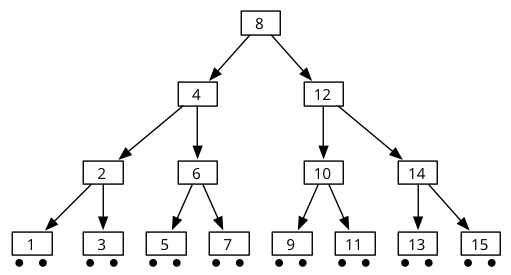
Exemple d'arbre de recherche

Initialement, la pile de nœuds contient, comme dit plus haut, les nœuds de l'arête gauche de l'arbre, à savoir [ 8, 4, 2, 1 ] (le sommet de la pile est l'élément souligné). Lors du premier appel à next, le nœud au sommet de la pile, 1, est dépilé puis retourné, mais avant cela l'arête gauche de son fils droit est empilée. Comme cette arête est vide, la pile contient maintenant [ 8, 4, 2 ]. Et ainsi de suite. La pile évolue donc de la manière suivante au cours de l'itération (chaque ligne représente un appel à next, et l'élément retourné par cet appel est celui au sommet de la pile, qui est souligné) :

8, 4, 2, 1
8, 4, 2
8, 4, 3
8, 4
8, 6, 5
8, 6
8, 7
8
12, 10, 9
12, 10
12, 11
12
14, 13
14
15

Comme on le constate, cette technique de parcours produit les éléments dans l'ordre croissant. Elle est plus efficace que celle consistant à transformer l'ensemble en arbre car chaque nœud n'est visité qu'une fois, et la taille de la pile ne dépasse jamais la profondeur de l'arbre.