Flame Maker – Etape 2 – Dessinateur IFS
Introduction
Le but de cette étape est d'écrire un programme permettant de générer des images monochromes de fractales IFS. Ces fractales sont à la base des fractales Flame.
Fractales IFS
Introduction
Pour mémoire, une fractale IFS est caractérisée par un ensemble de \(n\) transformations affines \(\{ F_1,\, F_2,\, \ldots,\, F_n \}\). La fractale elle-même est l'ensemble de points \(S\) satisfaisant l'équation : \[ S = \bigcup_{i=1}^n F_i(S). \] On peut obtenir une image monochrome à partir d'un tel ensemble \(S\) simplement en coloriant tous les points en faisant partie.
Plusieurs algorithmes existent pour calculer l'ensemble \(S\) à partir des fonctions affines caractérisant la fractale. Celui utilisé pour ce projet se nomme algorithme du chaos et consiste à calculer la suite suivante de points \(p_j\) avec \(j\) allant de 0 à une valeur maximale \(m\) donnée : \[ p_0 = (0,0),\ p_1 = F_{i_1}(p_0),\ p_2 = F_{i_2}(p_1),\ \ldots,\ p_{m} = F_{i_m}(p_{m-1}) \] où \(i_1 \ldots i_m\) sont des entiers aléatoires compris entre \(1\) et \(n\), le nombre de transformations caractérisant la fractale. En d'autres termes, un élément de la suite est calculé en appliquant à l'élément précédent une des fonctions caractérisant la fractale, choisie de manière aléatoire.
Une fois cette suite calculée, l'ensemble \(S\) est simplement défini comme étant composé des éléments de cette suite amputée de ses \(k\) premiers éléments (où \(k\) vaut p.ex. 20) : \[ S = \{ p_{k}, p_{k+1}, \ldots, p_{m} \} \]
Mise en œuvre Java
Fractale
La classe IFS du paquetage ch.epfl.flamemaker.ifs modélise les fractales IFS. Cette classe est non modifiable et équipée d'un seul champ privé et non modifiable de type List<AffineTransformation> (où List est l'interface de l'API Java, qui se trouve dans le paquetage java.util) contenant les transformations affines caractérisant la fractale.
La classe IFS est équipée du seul constructeur suivant :
IFS(List<AffineTransformation> transformations), qui construit une fractale caractérisée par les transformations données. La liste de transformations doit absolument être copiée par le constructeur pour garantir l'immuabilité de la fractale.
Cette classe possède de plus une seule méthode publique :
IFSAccumulator compute(Rectangle frame, int width, int height, int density), qui calcule, au moyen de l'algorithme du chaos, la fractale dans la région du plan délimitée par le cadreframeet stocke le résultat dans un nouvel accumulateur de largeurwidthet hauteurheight, qui est retourné. Le nombre d'itérations à effectuer est calculé en fonction du paramètredensity, comme expliqué plus bas.
Le fonctionnement de cette méthode est détaillé dans les sections qui suivent.
Algorithme du chaos
En pseudo-code, l'algorithme du chaos peut s'exprimer ainsi :
p = (0, 0)
répéter 20 fois
i = entier aléatoire uniformément distribué entre 0 et n-1
p = F[i](p)
S = {}
répéter m fois
i = entier aléatoire uniformément distribué entre 0 et n-1
p = F[i](p)
ajouter p à S
La programmation de cet algorithme en Java ne pose pas de problème particulier. Trois questions se posent toutefois :
- Comment choisir un entier aléatoire uniformément distribué dans un intervalle donné ?
- Comment représenter l'ensemble
S? - Quelle valeur faut-il choisir pour
m, le nombre d'itérations à effectuer ?
Les sections ci-dessous répondent à ces questions.
Entiers aléatoires
La solution la plus simple pour produire des entiers (pseudo-)aléatoires consiste à utiliser la classe java.util.Random de l'API Java. Une fois une instance de la classe Random créée, il suffit d'appeler sa méthode nextInt pour obtenir un nouvel entier uniformément distribué entre 0 et la valeur passée en argument, cette dernière n'étant pas incluse.
Ensemble des points
Une manière de représenter l'ensemble \(S\) serait d'utiliser une des classes implémentant l'interface Set de l'API Java, qui modélise des ensembles mathématiques. Toutefois, représenter l'ensemble \(S\) n'est pas vraiment nécessaire ici, puisque le but final est de produire une image. Ainsi, au lieu de calculer l'ensemble \(S\), on peut calculer directement l'image finale, ou quelque chose qui s'en approche.
Lors de l'exécution de l'algorithme du chaos, on stocke donc uniquement une information booléenne pour chaque pixel de l'image finale, qui dit si la zone du plan correspondant à ce pixel contient au moins un point de \(S\). Cette information est stockée dans un objet nommé accumulateur, qui est une grille de cases, chacune des cases correspondant à un pixel de l'image finale. Les cases contiennent pour l'instant une simple valeur booléenne, qui est vraie si et seulement si au moins un point de \(S\) se trouve dans la zone du plan correspondant à la case. Lors des étapes suivantes, des informations plus détaillées seront stockées dans les cases, afin de pouvoir produire des images en niveaux de gris d'abord, puis en couleur ensuite.
L'image ci-dessous montre une partie du plan, un ensemble de points du plan et un accumulateur de 6×5 cases. Le cadre de l'accumulateur, c-à-d le rectangle du plan qu'il couvre, est représenté en gras. Les cases grisées sont celles qui contiennent au moins un point de l'ensemble \(S\), et dont le booléen est donc vrai. Les cases sont identifiées par leurs coordonnées (entières), et la case de coordonnées (0,0) se trouve en bas à gauche, conformément aux conventions mathématiques. Six points se trouvent en dehors du cadre de l'accumulateur et n'ont aucun effet sur celui-ci.1
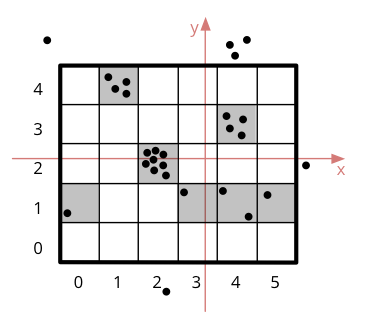
Le plan, un ensemble de points du plan et un accumulateur
En Java, l'accumulateur est modélisé par la classe non modifiable IFSAccumulator. Cette classe n'est pas grand-chose d'autre qu'un tableau bi-dimensionnel de booléens encapsulé de façon à être non modifiable. Elle possède donc un unique champ privé et non modifiable de type boolean[][] contenant les éléments de l'accumulateur. Elle possède le constructeur suivant :
IFSAccumulator(boolean[][] isHit), qui construit un accumulateur avec le tableau bi-dimensionnel donné. Ce tableau doit absolument être copié en profondeur par le constructeur afin de garantir l'immuabilité de l'accumulateur.
L'accumulateur est de plus équipé des méthodes suivantes :
int width(), qui retourne la largeur (en nombre de cases) de l'accumulateur.int height(), qui retourne la hauteur (en nombre de cases) de l'accumulateur.boolean isHit(int x, int y), qui retourne vrai si et seulement si la case de l'accumulateur aux coordonnées données contient au moins un point de \(S\) (on dit alors que la case a été touchée, d'où le nom de la méthode). Lève l'exceptionIndexOutOfBoundsExceptionsi l'une des deux coordonnées est invalide.
La classe IFSAccumulator étant non modifiable, il est nécessaire d'avoir un moyen de créer progressivement son contenu lors de l'exécution de l'algorithme du chaos. Pour cela, une classe séparée, nommée IFSAccumulatorBuilder, existe2. Son but est de construire progressivement un IFSAccumulator. Cette classe est équipée d'un seul constructeur :
IFSAccumulatorBuilder(Rectangle frame, int width, int height), qui produit un bâtisseur d'accumulateur pour la région du plan délimitée par le cadreframe, de largeurwidthet hauteurheight(en nombre de cases). Lève l'exceptionIllegalArgumentExceptionsi la largeur ou la hauteur n'est pas strictement positive (c-à-d supérieure à zéro).
Cette classe possède également les méthodes suivantes :
void hit(Point p), qui met à vrai la case de l'accumulateur correspondant au point du plan donné. Ne fait rien si le point est en dehors de la région du plan couverte par l'accumulateur, c-à-d le cadreframepassé au constructeur de cette classe.IFSAccumulator build(), qui retourne un accumulateur contenant les points collectés jusqu'à présent.
Conseils de programmation :
- Dans la méthode
hit, vous aurez probablement besoin d'obtenir la partie entière par défaut d'un nombre, ce qui peut se faire au moyen de la méthode statiquefloorde la classeMathdu paquetagejava.lang. - Pour obtenir les coordonnées de la case de l'accumulateur contenant un point, il faut passer des coordonnées du plan aux coordonnées de l'accumulateur. Une manière de le faire est de calculer, lors de la construction du bâtisseur d'accumulateur, la transformation (affine) permettant d'effectuer ce changement de coordonnées, puis d'utiliser cette transformation dans la méthode
hitpour déterminer la case de l'accumulateur affectée par le point reçu. Voilà une occasion d'utiliser votre classeAffineTransformationdans un autre contexte que la fractale IFS elle-même.
Nombre d'itérations
Il semble logique que le nombre d'itérations à effectuer dépende du nombre de cases de l'accumulateur : plus l'accumulateur est grand, et plus le nombre d'itérations de l'algorithme du chaos doit l'être également.
La méthode compute prend donc un paramètre nommé densité à partir duquel le nombre d'itérations à effectuer \(m\) est calculé, selon la formule suivante :
\[
m = d\times w\times h
\]
où \(d\) est la densité, \(w\) la largeur de l'accumulateur (en nombre de cases) et \(h\) sa hauteur (en nombre de cases).
Images PBM
Introduction
Le moyen le plus simple de voir si la méthode compute de la classe IFS fonctionne est de produire une image et de la visualiser. Pour simplifier cette étape, l'image est produite dans un fichier dont le contenu est ensuite visualisé par un programme externe.
Il existe une pléthore de formats de fichiers d'image dotés de différents avantages et inconvénients. Pour cette étape vous utiliserez le format PBM qui a l'avantage d'être extrêmement simple et l'inconvénient d'être terriblement gourmand en taille.
Format de fichier
Le format PBM est un format textuel très simple permettant de décrire des images monochromes. Le fichier est structuré ainsi :
- La première ligne contient la chaîne
P1qui identifie ce type de fichiers. - La seconde ligne contient la largeur et la hauteur de l'image, séparés par une espace.
- Les lignes qui suivent contiennent les lignes de l'image. Chaque ligne est constituée d'une suite de caractères
0(représentant un pixel blanc) et1(représentant un pixel noir) séparés par une ou plusieurs espaces.
Attention, les lignes sont ordonnées de haut en bas, c'est-à-dire dans la direction opposée à celle utilisée en mathématique ! Il faut en tenir compte lors de la génération du fichier pour obtenir une image correcte.
Par exemple, une image de largeur 6 et de hauteur 10 représentant la lettre J peut être représentée par le fichier suivant :
P1 6 10 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Mise en œuvre Java
Etant donné que la production d'images PBM n'est qu'un moyen de tester le dessinateur IFS et pas le but final de ce projet, le code permettant de générer une image PBM à partir d'un accumulateur peut être placé dans une méthode statique de la classe contenant également la méthode main pour cette étape. La méthode main peut construire quelques fractales IFS de test (voir ci-dessous), les calculer au moyen de la méthode compute puis produire un fichier PBM pour chacune d'elles au moyen de la méthode statique évoquée à l'instant.
Pour créer un fichier et y écrire des données, il faut à nouveau passer par l'API Java, en l'occurrence la classe java.io.PrintStream.
La classe PrintStream permet de créer un flôt de sortie (output stream en anglais) dans lequel il est possible d'imprimer des objets quelconques. Nous utiliserons ici uniquement la possibilité d'y écrire des chaînes de caractères.
La classe PrintStream possède plusieurs constructeurs, dont un qui prend un nom de fichier en argument. Ce fichier est créé au besoin, et il est ensuite possible d'y écrire des chaînes de caractères au moyen des méthodes print et println. A noter que vous connaissez déjà ces méthodes, puisque l'objet System.out est une instance de PrintStream et vous avez déjà certainement utilisé un appel à System.out.println pour afficher quelque chose à l'écran !
Une fois le contenu écrit dans le fichier PBM, il est important de penser à appeler la méthode close pour fermer le flôt.
Visualisation des images
Pour visualiser les images, vous pouvez par exemple utiliser un des programmes suivants, en fonction de votre système d'exploitation :
- Pour Mac OS : Xee (attention, ce programme inverse les couleurs des images PBM et affiche en blanc les pixels qui devraient être noirs, et inversément).
- Pour Linux : la commande
displayde ImageMagick. - Pour Windows : la commande
imdisplayde ImageMagick.
Une autre option consiste à convertir l'image PBM en un format plus facilement reconnu par les systèmes d'exploitation modernes, comme PNG. Pour ce faire, il est par exemple possible d'utiliser un des convertisseurs en ligne suivants :
Test
Pour tester votre programme, vous pouvez vérifier que vous obtenez bien les images attendues pour les deux fractales connues ci-dessous.
Le triangle de Sierpinski
Le triangle de Sierpinski peut s'obtenir au moyen de trois fonctions affines spécifiées par les matrices suivantes :
\[ A_1 = \begin{pmatrix} 0.5 & 0 & 0\\ 0 & 0.5 & 0\\ 0 & 0 & 1 \end{pmatrix} \] \[ A_2 = \begin{pmatrix} 0.5 & 0 & 0.5\\ 0 & 0.5 & 0\\ 0 & 0 & 1 \end{pmatrix} \] \[ A_3 = \begin{pmatrix} 0.5 & 0 & 0.25\\ 0 & 0.5 & 0.5\\ 0 & 0 & 1 \end{pmatrix} \]
Le cadre à utiliser pour dessiner ce triangle (c-à-d le paramètre frame à passer à la méthode compute) est un carré centré en (0.5, 0.5) et de côté 1. L'image obtenue pour ce cadre, un accumulateur de 100 pixels de côté et une densité de 1 est présentée ci-dessous.

Le triangle de Sierpinski
La fougère de Barnsley
Une fractale ressemblant à une fougère peut s'obtenir au moyen de quatre fonctions affines spécifiées par les matrices suivantes :
\[ A_1 = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0.16 & 0\\ 0 & 0 & 1 \end{pmatrix} \] \[ A_2 = \begin{pmatrix} 0.2 & -0.26 & 0\\ 0.23 & 0.22 & 1.6\\ 0 & 0 & 1 \end{pmatrix} \] \[ A_3 = \begin{pmatrix} -0.15 & 0.28 & 0\\ 0.26 & 0.24 & 0.44\\ 0 & 0 & 1 \end{pmatrix} \] \[ A_4 = \begin{pmatrix} 0.85 & 0.04 & 0\\ -0.04 & 0.85 & 1.6\\ 0 & 0 & 1 \end{pmatrix} \]Le cadre à utiliser pour dessiner cette fougère est un rectangle centré en (0, 4.5), de largeur 6 et de hauteur 10. L'image obtenue pour ce cadre, un accumulateur de 120 pixels de large et 200 de haut et une densité de 150 est présentée ci-dessous.

La fougère de Barnsley
Résumé
Pour cette étape, vous devez :
- Ecrire les classes
IFS,IFSAccumulatoretIFSAccumulatorBuilderdu paquetagech.epfl.flamemaker.ifsen fonction des spécifications ci-dessus. - Ecrire une classe principale (nommée p.ex.
IFSMaker) dans le même paquetage, équipée d'une méthodemainqui calcule les fractales IFS de test décrites ci-dessus et produise les images correspondantes dans des fichiers au format PBM. Le code de création du fichier devrait idéalement être placé dans une méthode statique auxiliaire afin de pouvoir facilement générer plusieurs fractales. - Vérifier que ces images correspondent à celles données ci-dessus et corriger les éventuels problèmes.
Mises à jour
- 20/02: Le cadre à utiliser pour la fougère a été corrigé.
Notes
1 Les personnes connaissant le fonctionnement d'un capteur d'appareil photo numérique auront peut-être constaté une ressemblance entre un tel capteur et l'accumulateur. Les points calculés lors de l'algorithme du chaos jouent ici le rôle des photons, tandis que les cases de l'accumulateur jouent le rôle des photosites du capteur.
2 L'idée de séparer la classe IFSAccumulator en deux parties, avec d'un côté un bâtisseur (builder en anglais) modifiable et de l'autre un accumulateur non modifiable est utilisée très fréquemment lorsqu'on désire pouvoir construire un objet en plusieurs étapes avant de l'utiliser de manière non modifiable. On retrouve p.ex. cette idée dans l'API Java avec la classe String (non modifiable) et son bâtisseur associé StringBuilder.