Flame Maker – Etape 1 – Géométrie 2D
Introduction
Le but de cette première étape est d'écrire et de tester des classes et interfaces permettant de représenter les entités géométriques à deux dimensions (2D) nécessaires au projet. Ces entités géométriques sont au nombre de trois :
- les points,
- les rectangles,
- les transformations.
Toutes les classes représentant ces entités sont non modifiables1.
Notez que l'API Java fournit déjà des classes pour représenter ces entités géométriques. Vous n'utiliserez toutefois pas ces classes ici, d'une part car elles souffrent de quelques défauts comme le fait d'être modifiables, et d'autre part car il est pédagogiquement intéressant de programmer ces classes.
Organisation en paquetages
La totalité du code du projet sera placée dans le paquetage ch.epfl.flamemaker et ses sous-paquetages.
Toutes les classes et interfaces de cette étape seront placées dans le sous-paquetage ch.epfl.flamemaker.geometry2d, réservé aux entités géométriques en deux dimensions.
Pour créer ce paquetage dans Eclipse, utilisez le menu File > New > Package puis entrez son nom, à savoir ch.epfl.flamemaker.geometry2d. Ensuite, pour créer une classe (ou interface) à l'intérieur de ce paquetage, sélectionnez-le dans l'explorateur de paquetages puis utilisez le menu File > New > Class. Eclipse vous proposera alors automatiquement de créer la classe dans ce paquetage et se chargera ensuite de créer les répertoires nécessaires et d'y placer les fichiers, et insérera l'énoncé package approprié au sommet du fichier.
Points
Concept mathématique
En deux dimensions, un point est caractérisé par deux coordonnées dans un système de coordonnées choisi. Deux systèmes de coordonnées sont utilisés dans ce projet :
- Le système cartésien, dans lequel un point est caractérisé par la composante parallèle à l'abscisse \(x\) et la composante parallèle à l'ordonnée \(y\) de sa distance à une origine \(O\).
- Le système polaire, dans lequel un point est caractérisé par sa distance \(r\) à une origine \(O\) et l'angle \(\theta\) entre l'abscisse et la ligne le reliant cette origine.
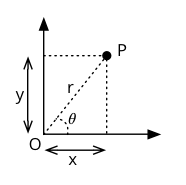
Un point et ses coordonnées cartésiennes et polaires
Mise en œuvre Java
La classe Point du paquetage ch.epfl.flamemaker.geometry2d modélise les points. Cette classe est équipée de deux champs privés et non modifiables de type double contenant les coordonnées cartésiennes \(x\) et \(y\) du point. D'autre part, cette classe est équipée d'un constructeur public :
Point(double x, double y), qui construit un point étant données ses coordonnées cartésiennes.
La classe Point possède également les méthodes publiques suivantes :
double x(), qui retourne la coordonnée cartésienne \(x\) du point.double y(), qui retourne la coordonnée cartésienne \(y\) du point.double r(), qui retourne la coordonnée polaire \(r\) du point.double theta(), qui retourne la coordonnée polaire \(\theta\) du point.String toString(), qui retourne une représentation textuelle du point, composée de ses coordonnées cartésiennes \(x\) et \(y\) séparées par une virgule et entourées de parenthèses, p.ex.(1.2,5.3)pour le point (1.2, 5.3).
Finalement, la classe Point possède un champ statique public et non modifiable :
Point ORIGIN, qui contient le point de coordonnées (0, 0).
Conseil de programmation : pour écrire la méthode theta, aidez-vous de la méthode atan2 de la classe java.lang.Math.
Rectangles
Concept mathématique
Les rectangles utilisés dans ce projet ont tous la particularité d'être parallèles aux axes (abscisse et ordonnée). Il s'agit donc de la seule sorte de rectangles considérée ici.
Un rectangle parallèle aux axes peut être caractérisé de différentes manières, par exemple par son centre (un point) et deux dimensions : la largeur (longueur du côté parallèle à l'abscisse) et la hauteur (longueur du côté parallèle à l'ordonnée). C'est cette caractérisation qui sera utilisée dans ce projet.
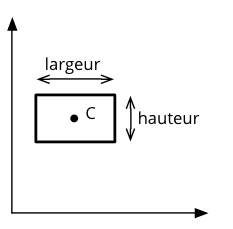
Un rectangle, son centre et ses dimensions
Mise en œuvre Java
La classe Rectangle du paquetage ch.epfl.flamemaker.geometry2d modélise les rectangles parallèles aux axes2. Elle est équipée de trois champs privés et non modifiables : le premier, de type Point, est le centre du rectangle ; les deux autres, de type double, sont la largeur et la hauteur du rectangle.
La classe Rectangle possède un seul constructeur public :
Rectangle(Point center, double width, double height), qui construit un rectangle étant donné son centre, sa largeur et sa hauteur ; lève l'exceptionIllegalArgumentExceptionsi la largeur ou la hauteur sont négatives ou nulles.
Elle possède de plus les méthodes publiques suivantes :
double left(), qui retourne la plus petite coordonnée \(x\) du rectangle.double right(), qui retourne la plus grande coordonnée \(x\) du rectangle.double bottom(), qui retourne la plus petite coordonnée \(y\) du rectangle.double top(), qui retourne la plus grande coordonnée \(y\) du rectangle.double width(), qui retourne la largeur du rectangle.double height(), qui retourne la hauteur du rectangle.Point center(), qui retourne le centre du rectangle.boolean contains(Point p), qui retourne vrai si et seulement si le pointpse trouve à l'intérieur du rectangle. Par définition, un point est considéré comme étant à l'intérieur d'un rectangle si et seulement si sa coordonnée \(x\) est supérieure ou égale à la plus petite coordoonée \(x\) et strictement inférieure à la plus grande coordonnée \(x\) du rectangle, et si sa coordonnée \(y\) est supérieure ou égale à la plus petite coordonnée \(y\) et strictement inférieure à la plus grande coordonnée \(y\) du rectangle. Notez qu'avec cette définition, un rectangle ne contient qu'un seul de ses coins, le coin bas-gauche3.double aspectRatio(), qui retourne le rapport largeur/hauteur du rectangle.Rectangle expandToAspectRatio(double aspectRatio), qui retourne le plus petit rectangle ayant le même centre que le récepteur, le rapport largeur/hauteuraspectRatioet contenant totalement le récepteur (c-à-d que tout point contenu dans le récepteur est également contenu dans le rectangle retourné). Lève l'exceptionIllegalArgumentExceptionsi le rapport passé est négatif ou nul.String toString(), qui retourne la représentation textuelle du rectangle, composée de la représentation textuelle du centre, de la largeur et de la hauteur séparés par une virgule et entourés de parenthèses. P.ex. le rectangle centré à l'origine, de largeur 2 et hauteur 1 a comme représentation textuelle la chaîne((0,0),2,1).
Transformations
Concept mathématique
Dans le cadre de ce projet, le terme transformation désigne une fonction faisant correspondre à tout point du plan un autre point du plan. En d'autres termes, une transformation est une fonction \(F: ℝ^2 \rightarrow ℝ^2\).
Au moyen de l'opérateur de composition de fonctions classique, il est possible de composer deux transformations pour en obtenir une nouvelle. Par exemple, si \(F\) et \(G\) sont deux transformations, leur composition \(F\circ G\) est la transformation définie de la manière standard : \((F\circ G)(x, y) = F(G(x, y))\).
Les transformations jouent un rôle central dans ce projet, puisque les fractales IFS sont composées d'un ensemble de transformations affines, auxquelles les fractales Flame ajoutent des transformations plus générales appelées variations.
Mise en œuvre Java
Les transformations au sens général sont représentées par une interface, et les différents types de transformations (affines ou plus générales pour les variations) sont représentés par des classes implémentant cette interface. Les transformations affines sont les seules sortes de transformations définies dans le cadre de cette étape, les autres le seront lors de prochaines étapes.
L'interface Transformation du paquetage ch.epfl.flamemaker.geometry2d modélise le concept de transformation. Cette interface est très simple puisqu'elle comporte l'unique méthode suivante :
Point transformPoint(Point p), qui retourne le pointptransformé.
Transformations affines
Concept mathématique
On appelle transformation affine toute transformation \(F: ℝ^2 \rightarrow ℝ^2\) ayant la forme suivante : \[ F(x, y) = (ax + by + c, dx + ey +f) \] où les coefficients \(a\), \(b\), \(c\), \(d\), \(e\) et \(f\) sont des nombres réels.
La notation matricielle est particulièrement adaptée aux transformations affines. En l'utilisant, on peut récrire la définition ci-dessus ainsi : \[ F(\vec{x}) = A\vec{x} + \vec{b} \] où \[ A = \begin{pmatrix} a & b\\ d & e \end{pmatrix},\ \vec{x} = \begin{pmatrix} x\\ y \end{pmatrix},\ \vec{b} = \begin{pmatrix} c\\ f \end{pmatrix}. \] La transformation \(F\) est alors caractérisée par la matrice \(A\) et le vecteur \(\vec{b}\). Il est toutefois possible de combiner ces deux éléments en une unique matrice de plus grande dimension construite de la manière suivante : \[ A_h = \left( \begin{array}{c|c} A & \vec{b}\\ \hline \vec{0}^\top & 1 \end{array} \right) = \begin{pmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1 \end{pmatrix} \] Si l'on prend soin d'augmenter aussi le vecteur \(\vec{x}\) ainsi : \[ \vec{x_h} = \begin{pmatrix} \vec{x}\\ 1 \end{pmatrix} = \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} \] on peut alors récrire la transformation \(F\) comme suit : \[ F(\vec{x_h}) = A_h \vec{x_h} \] Cette nouvelle formulation utilise ce que l'on appelle les coordonnées homogènes. Ces coordonnées ont de nombreuses propriétés intéressantes qui font qu'elles sont souvent employées en géométrie. Parmi ces propriétés figure le fait que la composition de deux transformations affines s'obtient simplement en multipliant leurs matrices homogènes. En d'autres termes, soient \(F\) et \(G\) deux transformations affines définies ainsi : \[ F(\vec{x_h}) = A_h\vec{x_h},\ G(\vec{x_h}) = B_h\vec{x_h} \] leur composition s'obtient ainsi : \[ (F\circ G)(\vec{x_h}) = (A_h\cdot B_h)(\vec{x_h}) \] A partir de dorénavant, seules les coordonnées homogènes seront utilisées, et le suffixe \(h\) sera omis pour alléger la notation.
Transformations de base
Les matrices homogènes pour un certain nombre de transformations de base s'obtiennent très facilement. Les transformations utilisées dans ce projet et leur matrice sont les suivantes :
- Translation de \(x\) unités parallélement à l'abscisse et \(y\) unités parallélement à l'ordonnée :
\begin{pmatrix} 1 & 0 & x\\ 0 & 1 & y\\ 0 & 0 & 1 \end{pmatrix}
- Rotation d'angle \(\theta\) (en radians) autour de l'origine :
\begin{pmatrix} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0\\ 0 & 0 & 1 \end{pmatrix}
- Dilatation d'un facteur \(s_x\) parallélement à l'abscisse et d'un facteur \(s_y\) parallélement à l'ordonnée :
\begin{pmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{pmatrix}
- Transvection d'un facteur \(s_x\) parallélement à l'abscisse :
\begin{pmatrix} 1 & s_x & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}
- Transvection d'un facteur \(s_y\) parallélement à l'ordonnée :
\begin{pmatrix} 1 & 0 & 0\\ s_y & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}
Mise en œuvre Java
La classe AffineTransformation du paquetage ch.epfl.flamemaker.geometry2d représente les transformations affines. Elle comporte six champs privés et non modifiables de type double contenant les six éléments variables de la matrice homogène. La classe implémente bien entendu l'interface Transformation décrite précédemment. Elle offre un unique constructeur :
AffineTransformation(double a, double b, double c, double d, double e, double f), qui construit une transformation affine étant donnés les éléments variables de la matrice.
De plus, la classe offre un certain nombre de méthodes publiques statiques permettant de construire facilement différents types de transformations affines :
AffineTransformation newTranslation(double dx, double dy), qui crée une transformation affine représentant une translation dedxunités parallélement à l'abscisse etdyunités parallélement à l'ordonnée.AffineTransformation newRotation(double theta), qui crée une transformation représentant une rotation d'angletheta(en radians) autour de l'origine.AffineTransformation newScaling(double sx, double sy), qui crée une transformation représentant une dilatation d'un facteursxparallélement à l'abscisse et d'un facteursyparallélement à l'ordonnée.AffineTransformation newShearX(double sx), qui crée une transformation affine représentant une transvection d'un facteursxparallélement à l'abscisse.AffineTransformation newShearY(double sy), qui crée une transformation affine représentant une transvection d'un facteursyparallélement à l'ordonnée.
La classe AffineTransformation possède également un champ statique public non modifiable :
AffineTransformation IDENTITY, qui contient la transformation identité.
Finalement, elle offre les méthodes suivantes :
Point transformPoint(Point p), qui retourne le pointptransformé par cette transformation (méthode de l'interfaceTransformation).double translationX(), qui retourne la composante horizontale de la translation, c-à-d l'élément \(c\) de la matrice.double translationY(), qui retourne la composante verticale de la translation, c-à-d l'élément \(f\) de la matrice.AffineTransformation composeWith(AffineTransformation that), qui retourne la composition de cette transformation affine avec la transformation affinethat.
A noter qu'il aurait pu être intéressant de définir la composition de transformations (c-à-d la méthode composeWith) au niveau de l'interface Transformation, puisqu'il est mathématiquement possible de composer n'importe quelle paire de transformations. Cela n'a pas été fait car seule la composition de transformations affines est nécessaire dans ce projet.
Tests
Une fois les classes Point, Rectangle et AffineTransformation écrites, il importe de les tester. Pour ce faire, vous utiliserez la bibliothèque JUnit qui facilite l'écriture de tests dits unitaires et qui est bien intégrée à Eclipse.
Comme son nom l'indique, un test unitaire ne teste qu'une unité bien définie du programme, p.ex. une classe ou un petit groupe de classes, de manière isolée. Pour vous familiariser avec ce concept, lisez le chapitre intitulé Tests unitaires du livre Introduction au test logiciel. Une fois la lecture terminée, téléchargez le fichier RectangleTest.java que nous vous fournissons et ajoutez-le à votre projet Eclipse. Ce fichier contient un test unitaire pour la classe Rectangle de l'étape courante.
Exécutez ce test directement depuis Eclipse en le sélectionnant puis en choisissant le menu Run > Run As > JUnit Test. Si tout se passe bien, vous devriez voir apparaître une fenêtre intitulée JUnit donnant le nombre de tests effectués, et le nombre de succès et d'échecs. Si vous constatez que certains tests échouent, corrigez votre classe Rectangle en fonction.
En vous inspirant de cette classe RectangleTest, écrivez des classes PointTest et AffineTransformationTest pour tester les classes Point et AffineTransformation.
Résumé et notes
Pour cette étape, vous devez :
- Ecrire les classes et interfaces
Point,Rectangle,TransformationetAffineTransformationdu paquetagech.epfl.flamemaker.geometry2den fonction des spécifications ci-dessus. - Ecrire des classes de test
PointTestetAffineTransformationTestqui testent les classes correspondantes en s'aidant de la bibliothèque JUnit. - Exécuter les tests et, le cas échéant, corriger les problèmes trouvés.
S'il vous reste du temps à disposition, vous pouvez l'utiliser pour vous familiariser avec un outil de gestion de version, comme suggéré dans l'introduction du projet. Cela vous permettra de travailler plus efficacement lors des prochaines étapes.
Mises à jour
- 19/02: Les deux dimensions des rectangles doivent être strictement positives. (Le fichier
RectangleTest.javaque nous vous fournissons a été mis à jour pour en tenir compte, pensez à le télécharger à nouveau).
Notes
1 De manière générale, toute classe modélisant une entité mathématique devrait être non modifiable, car les opérations mathématiques ne modifient jamais les entités sur lesquelles elles travaillent. Par exemple, lorsqu'on multiplie deux nombres, il est clair qu'aucun des nombres multiplié n'est modifié. Il en va de même lorsqu'on multiplie deux matrices. Cela peut paraître évident, mais on trouve malheureusement encore beaucoup d'API qui violent cette règle, en particulier avec les matrices, pour de discutables raisons d'efficacité.
2 Etant donné que la classe Rectangle ne modélise que les rectangles ayant une certaine forme, à savoir ceux parallèles aux axes, un nom moins général que Rectangle aurait peut-être été préférable. Toutefois, la plupart des API existants utilisent le nom Rectangle, et cette convention a été reprise pour le projet.
3 Cette définition de l'appartenance d'un point à un rectangle peut paraître étrange mais a plusieurs avantages en pratique. Parmi ceux-ci, on peut citer le fait que si l'on place plusieurs rectangles côte-à-côte, aucun point n'appartient à plus de l'un d'entre-eux. Par exemple, les quatres carrés de côté 2 centrés en (-1, -1), (-1, 1), (1, -1) et (1, 1) sont contigüs mais avec la définition d'appartenance utilisée ici, l'origine n'appartient qu'à un seul de ces carrés, celui centré en (1, 1).