Le projet Flame Maker
Introduction
Le but du projet Flame Maker est de réaliser un programme de création et de visualisation d'images fractales de type Flame.
Ce document présente brièvement les principaux concepts du projet, puis donne un aperçu du programme à réaliser.
Les images fractales
Une image fractale est une image présentant un fort degré d'auto-similarité. C'est-à-dire que certains détails se retrouvent systématiquement dans l'image, quelle que soit l'échelle et la partie de l'image observée.
Un arbre est un exemple d'objet réel de nature fractale. Si on observe l'arbre dans son ensemble, on voit un tronc dont jaillissent de nombreuses grosses branches. En examinant une de ces grosses branches, on retrouve une structure similaire, puisque quantités de branches plus petites en jaillissent. Il en va ainsi jusqu'aux feuilles.
En infographie, on peut produire automatiquement des images fractales au moyen de formules mathématiques simples et généralement récursives. De telles formules sont ainsi souvent utilisées pour générer des images réalistes d'objets naturels comme des plantes, des nuages, des reliefs montagneux, etc. De plus, on peut les utiliser pour produire des images abstraites ayant certaines qualités esthétiques. C'est ce que vous allez faire dans ce projet qui se concentre sur un type particulier de fractales, nommé Flame, dérivé d'un autre type de fractales, les fractales IFS.
Les fractales IFS
Une fractale IFS (pour Iterated Function System) est caractérisée par un ensemble de \(n\) transformations affines1 \(\{ f_1,\, f_2,\, \ldots,\, f_n \}\), chacune d'entre-elles faisant correspondre un point du plan à un autre point du plan. La fractale elle-même est l'ensemble \(S\) des points satisfaisant l'équation : \[ S = \bigcup_{i=1}^n f_i(S). \] Différentes techniques existent pour déterminer \(S\), une d'entre-elles sera présentée plus tard dans le projet. Une fois un ensemble \(S\) calculé, on peut obtenir une image affichable à l'écran simplement en coloriant avec une couleur donnée tous les points faisant partie de \(S\).
Par exemple, la fractale IFS composée des trois transformations suivantes : \[ \begin{array}{rcl} f_1(x, y) & = & \left(\frac{x}{2}, \frac{y}{2}\right)\\ f_2(x, y) & = & \left(\frac{x + 1}{2}, \frac{y}{2}\right)\\ f_3(x, y) & = & \left(\frac{x + ½}{2}, \frac{y + 1}{2}\right)\\ \end{array} \] a pour image le fameux triangle de Sierpinski (les points faisant partie de \(S\) étant coloriés en noir) :

Le triangle de Sierpinski
Les fractales Flame
Les fractales Flame, conçues par Scott Draves, sont une extension des fractales IFS. Le but de Draves était de produire des images plus diverses et esthétiques que les fractales IFS, d'une part en étendant l'algorithme de base et d'autre part en affinant la technique de dessin.
Ainsi, en plus des transformations affines héritées des fractales IFS, les fractales Flame possèdent un ensemble de transformations prédéfinies plus générales, appelées variations, qui sont composées, de manière pondérée, avec les transformations affines.
D'autre part, la technique de dessin est affinée pour produire des images couleur et non plus monochromes comme pour les fractales IFS.
Les images ainsi obtenues peuvent être esthétiquement plaisantes, comme l'illustre l'exemple ci-dessous.

Une fractale Flame
Le programme Flame Maker
Le but de ce projet est de réaliser un programme nommé Flame Maker permettant à un utilisateur d'éditer interactivement les paramètres d'une fractale de type Flame et de visualiser l'image résultante.
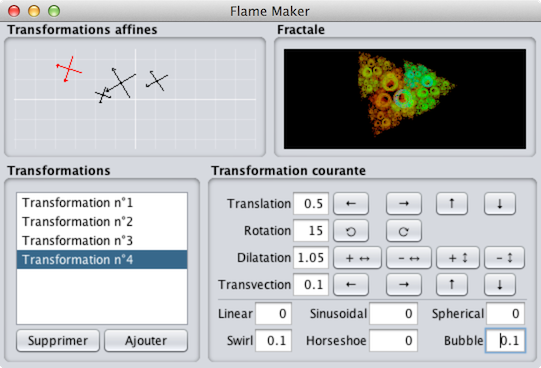
Le programme Flame Maker
L'interface utilisateur du programme, visible ci-dessus, est composée des quatre parties suivantes :
- En haut à gauche, une visualisation des transformations affines qui composent la fractale.
- En haut à droite, une visualisation de l'image de la fractale.
- En bas à gauche, la liste des transformations composant la fractale. Une de ces transformations est toujours sélectionnée.
- En bas à droite, des boutons permettant de modifier la partie affine de la transformation actuellement sélectionnée, et des champs permettant de modifier les poids des différentes variations (Linear, Sinusoidal, etc.) appliquées à cette transformation affine.
Notes
1 Une transformation affine est une transformation préservant la colinéarité (tout ensemble de points situés sur une ligne est transformé en un ensemble de points également situé sur une ligne) et le rapport des distances entre des points colinéaires.